A nearly 60-year-old mathematical problem has finally been solved.
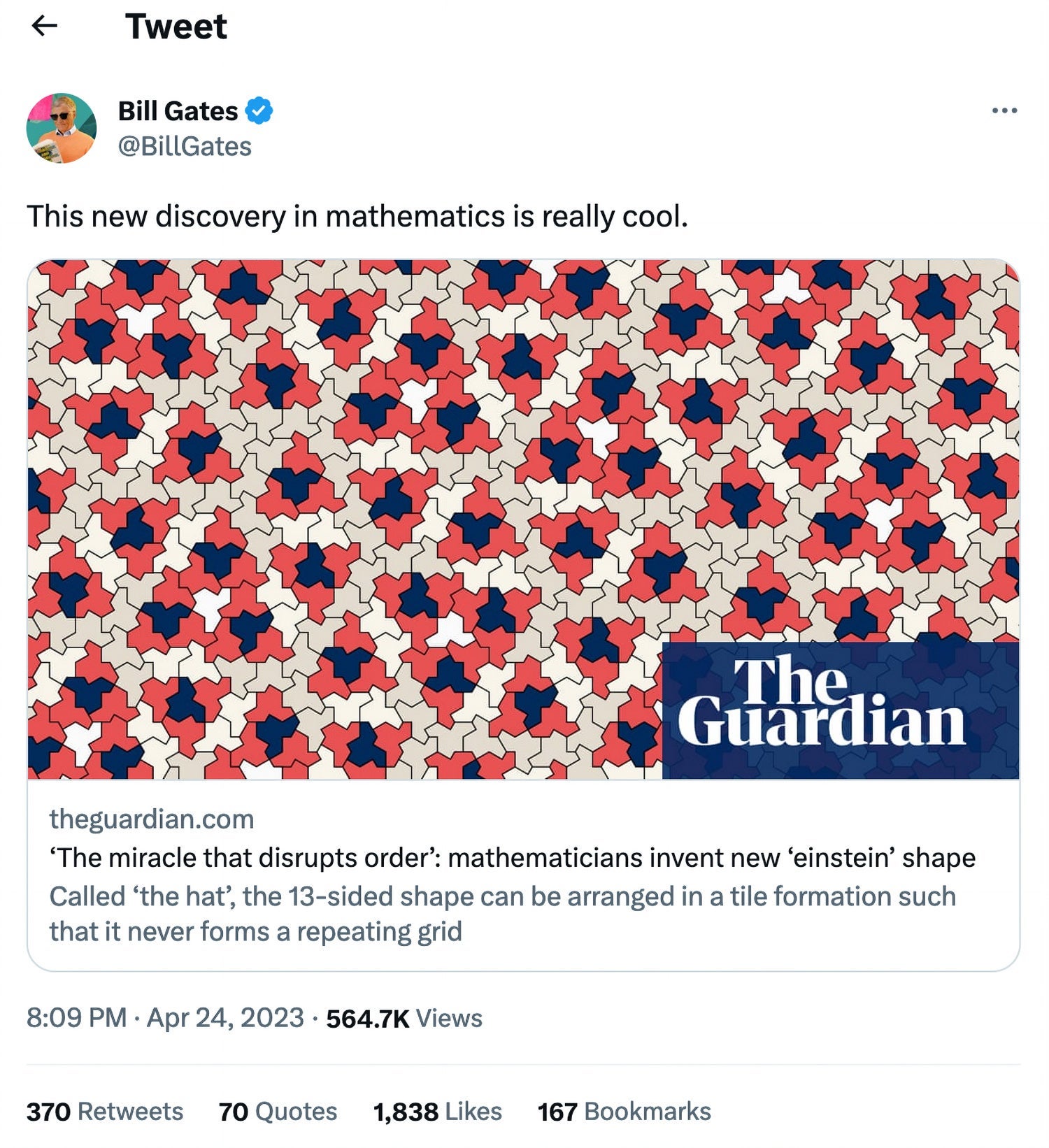
The story began last fall when David Smith, a retired print technician from Yorkshire, England, came upon a shape with a tantalizing property. The life-long tiling enthusiast discovered a 13-sided shape — dubbed the hat — that is able to fill the infinite plane without overlaps or gaps in a pattern that not only never repeats but also never can be made to repeat.
This elusive shape is known to mathematicians as an aperiodic monotile or an einstein, a clever pun that takes its name from the German words ein and stein that mean one stone.
“Dave and I had been in touch over the years and we belong to the same old-fashioned listserv for people interested in tiling, a mix of tiling enthusiasts, programmers and mathematicians,” recalls Cheriton School of Computer Science Professor Craig S. Kaplan, who collaborated with Smith, software developer Joseph Myers and mathematician Chaim Goodman-Strauss on the paper that has proven that the elusive einstein exists.
“Dave was on to something big, something historic, but he hit the wall on what he could deduce about this shape by working with paper cut-outs. He knew I had recently published a paper about a related topic for which I developed a piece of software that we could use to understand what his shape was doing. He sent me an email asking, ‘Hey, can you run this through your software and see what happens?’”
Professor
Craig
S.
Kaplan
holds
two
einstein
tiles,
a
13-sided
shape
he
and
his
collaborators
call
the
hat
that
can
tile
the
plane
indefinitely
without
the
pattern
ever
repeating.
Professor
Kaplan
is
interested
in
a
broad
range
of
interdisciplinary
topics,
with
a
particular
focus
on
interactions
between
mathematics
and
art.
He
uses
mathematical
ideas
to
create
tools
and
algorithms
that
generate
ornamental
patterns
and
that
empower
artists
and
designers.
His
work
incorporates
knowledge
from
computer
graphics,
classical
and
computational
geometry,
human-computer
interaction,
graph
theory,
symmetry
and
tiling
theory,
and
perceptual
psychology.
Read the full article on Waterloo News
Watch Professor Kaplan’s interview with Brady Haran of Numberphile about how this discovery came to be.
International coverage
Mass news media
- Elusive ‘Einstein’ Solves a Longstanding Math Problem, The New York Times, Siobhan Roberts
- ‘The miracle that disrupts order’: mathematicians invent new ‘einstein’ shape, The Guardian, Matthew Cantor
- Retired Yorkshireman solves elusive ‘Einstein tile’ maths problem, The Times, Tom Whipple
- Newly discovered ‘einstein’ shape can do something no other tile can do, CNN, Jacopo Prisco
Specialist publications, presentations and tweet of note
-
A groundbreaking new discovery in mathematics! The Hat, an aperiodic monotile, National Museum of Mathematics
-
A hat for Einstein (YouTube)
-
Meet the authors (YouTube)
-
- Hobbyist Finds Math’s Elusive ‘Einstein’ Tile, Quanta Magazine, Erica Klarreich
- Newfound Mathematical ‘Einstein’ Shape Creates a Never-Repeating Pattern, Scientific American, Manon Bischoff
- At Long Last, Mathematicians Have Found a Shape With a Pattern That Never Repeats, Smithsonian Magazine, Will Sullivan
- A geometric shape that does not repeat itself when tiled, Phys.org, Bob Yirka
- Mathematicians discover shape that can tile a wall and never repeat, New Scientist, Matthew Sparkes