Fascinating research that lies between neuroscience and artificial intelligence
Artificial neural networks have come to dominate the field of artificial intelligence. From self-driving cars to devices that recognize handwriting to interactive chatbots to astonishingly accurate online translators, artificial neural networks lie at the core of a staggering array recent AI developments.
Artificial neural networks are modelled loosely on the neuronal architecture of the brain, and they have been designed to simulate the way the brain processes information. Of all forms of artificial intelligence — and much like the human brain — artificial neural networks excel at finding patterns in data.

L to R: Nolan Shaw, a PhD student at the Cheriton School of Computer Science studying artificial intelligence, and his supervisor, Professor Jeff Orchard. Professor Orchard and his students form the Neurocognitive Computing Lab, where through computational experiments and mathematical analysis, they try to understand the neurological basis of perception, cognition and behaviour.
“In artificial neural networks you have nodes that are analogous to neurons in the brain and they are arranged in a hierarchy,” explains Nolan Shaw, a PhD student studying artificial intelligence at the Cheriton School of Computer Science. “An artificial neural network has layers — an input layer that’s connected to another layer called a hidden layer. There may be one or more hidden layers, then finally an output layer. If you want to learn some function that takes, say, n inputs and maps to p outputs, as long as you’re able to give examples of what the outputs should look like for a given input, the network can use an algorithm called backpropagation to adjust the connection weights — the strength of the connections between the neurons — so that eventually the network learns some function that ideally generalizes to solve this problem for all inputs.”
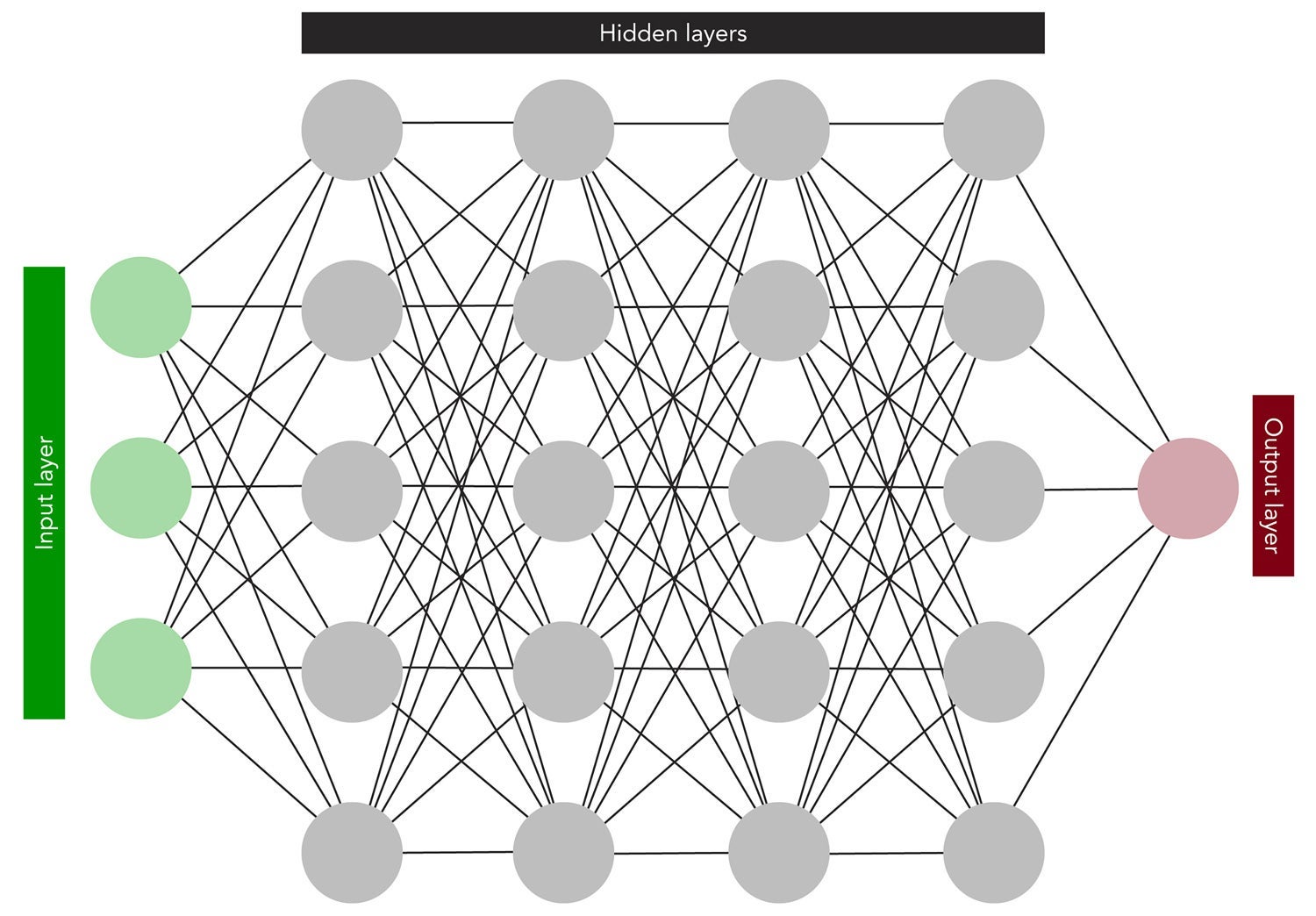
Basic
structure
of
an
artificial
neural
network.
Data
is
entered
at
the
input
layer,
then
passed
to
one
or
more
hidden
layers
consisting
of
processing
nodes
that
extract
certain
high-level
features.
Researchers
who
train
the
artificial
neural
network
can
give
labels
to
the
output
and
using
a
technique
known
as
backprop
—
short
for
error
backpropagation
—
help
perfect
the
output
results.
This
results
in
an
artificial
neural
network
that
when
given
new,
unfamiliar
data
can
reliably
recognize
human
faces
for
example
—
or
a
whole
host
of
other
things
the
network
has
been
trained
to
identify
or
classify.
In a simplified sense, the human brain works similarly by altering the number of synapses or neuronal junctions between neurons, strengthening connections and reinforcing pathways that have proven to be useful and pruning those that are not. By doing so, the brain more efficiently propagates and processes information.
While backprop works well in artificial neural networks, it’s not clear how our brains could implement it. Neurons are, after all, just little machines, and they can react only to signals from their immediate surroundings. That is, they can use only local information. No known method can move information around the brain the way the backprop algorithm does in a neural network.
Professor Orchard and members of his Neurocognitive Computing Lab work at the junction between AI and neuroscience, investigating neural-network algorithms that an actual brain could implement. And their realization that some processes in the brain happen locally became the inspiration for research on neural networks that Nolan and Professor Orchard have recently explored. In particular, they've investigated how individual neurons can regulate their activity in a way that improves learning across the entire network.
“Neurons in the brain alter their sensitivity continuously,” Nolan explained. “If a neuron is bombarded with lots of excitatory input, it will fire vigorously at first. But if it continues to receive the same stimulus, the neuron eventually dials downs it sensitivity. Conversely, if a neuron becomes starved for input, it will increase its sensitivity.”
Some previous studies have looked into developing a learning rule that biological neurons could feasibly adopt that would allow them to rest on the ideal firing rate regardless of the stimulus they receive, Nolan explained. “The motivation is twofold. One, and probably the reason it’s been largely overlooked previously in AI research, is that biological neurons settle on an ideal firing rate to preserve energy. In an artificial neural network, this is irrelevant because it takes the same amount of energy to store a zero as it would to store a one. But there’s a second benefit to finding the ideal firing rate. Very little information is transmitted by a neuron that is either not firing at all or firing near its maximum rate. In between those two extremes is an information sweet spot.”
Most research in artificial intelligence has focused on adjusting the learning weights between neurons in the network, rather than adjusting the sensitivity of each neuron to make it the most efficient signal propagating unit possible.
For an artificial neural network to operate efficiently and to extract the most information from its input data, its neurons need to operate in this sweet spot. Then, as the world of inputs runs through the network, each neuron exhibits a wide range of activity levels, a spread-out distribution of activity.
This is particularly important in artificial neural networks with several hidden layers, in what are known as deep neural networks. “When we’re talking about neural networks, typically you’re going to have a lot of nodes — as many as you need to represent your input properly — and with many hidden layers,” Nolan said. As information is propagated through the network from one layer to the next, the useable error signal declines, making it increasingly difficult to tune the parameters of earlier layers in the network. This issue is known as the vanishing gradient problem and it limits the learning potential of neural networks. One way of solving the vanishing gradient problem has been a technique known as batch normalization.
“Batch normalization takes inputs into a neuron and normalizes their distribution before the neuron had seen them, solving the vanishing gradient problem,” Nolan said. “Our method, which we’ve called intrinsic plasticity, also normalizes the distribution, but it also improves the information potential of a neuron’s activity and it doesn’t require looking forward in time.”
“The important thing here is that Nolan has found a way to do batch normalization locally in a neural network,” added Professor Orchard. “Unlike batch normalization, which normalizes the input to a neuron, intrinsic plasticity regulates the output of a neuron, which is closer to how real neurons behave.”
This is a tantalizing contribution to both neuroscience and to artificial intelligence because intrinsic plasticity not only improves learning in deep neural networks, but, importantly, it also provides a plausible explanation why biological neurons regulate their firing rate in response to the statistics of their stimuli.
For years, it’s been a conundrum why biological neurons tune themselves, Professor Orchard said. “They adjust their firing rate continuously to achieve a constant firing rate. Intrinsic plasticity provides a plausible explanation why that occurs, how neurons tune themselves.”
“In some ways, intrinsic plasticity does double duty,” Nolan adds. “First, it addresses why biological neurons tune themselves. The answer seems to be to improve informational efficiency. The other question is, how do biological brains perform something like batch normalization? Intrinsic plasticity provides a possible answer to that question as well.”
Nolan’s hope is that this contribution to artificial intelligence will also encourage other researchers to explore the mathematical and information theoretic principles that underlie how biological brains function.
“There may be much more mathematically principled processes in biological brains that people are not paying enough attention to,” Nolan said. “Finding a phenomenon that is consistent with the way biological neurons actually behave and then using information theory to describe why they might be doing that is going to be an important field of research. Information theory provides a lens to see what could be happening.”
It’s also provocative to think that despite the brain’s complexity perhaps a few simple theories of how neurons behave at a local level can explain its emergent computational power.
“Neuroscience and AI have been trying to find a ‘theory of evolution’ for the brain — in essence, an explanatory theory for how the brain works that’s analogous to Darwin’s theory of evolution through natural selection, which explains adaptation, complexity and diversity,” Professor Orchard said. “Darwin’s theory boils down to a few basic principles that explain so much. The brain is incredibly complex and comprised of billions and billions of neurons, but perhaps just a small number of rules or principles operate within it to create intelligence and cognition.”
To learn more about the research this feature article is based on, please see Shaw NP, Jackson T, Orchard J. 2020. Biological batch normalisation: How intrinsic plasticity improves learning in deep neural networks. PLoS ONE 15(9): e0238454.