6 Implementing functional languages
\(\newcommand{\la}{\lambda} \newcommand{\Ga}{\Gamma} \newcommand{\ra}{\rightarrow} \newcommand{\Ra}{\Rightarrow} \newcommand{\La}{\Leftarrow} \newcommand{\tl}{\triangleleft} \newcommand{\ir}[3]{\displaystyle\frac{#2}{#3}~{\textstyle #1}}\)
So far, we have used a simplified imperative language (SIMP) and a simplified machine instruction set and architecture (FIST) to discuss the difficulties of imperative programming without being bedevilled by the messy details of real implementations. We’ve written small interpreters and compilers in Racket to help understand why imperative languages look the way they do and what issues need to be addressed in designing and using them.
Going the other way, writing an interpreter or compiler for even something as simple as Faux Racket in an imperative language, seems a more daunting task. Racket gives us so much scope as an implementation platform that it’s hard to see how to achieve similar results in an imperative language. In the next two chapters, I’ll provide some details as to how to fill that gap. I won’t provide a complete blueprint, since neither SIMP nor FIST are full-featured enough to facilitate such work, and you’ll need to learn a real-world imperative language for that. But you’ll learn enough that Racket won’t seem like magic any more (it will still seem magical, though, because it is!).
In this chapter, I’ll focus on what we might see if we could monitor the contents of memory while a Racket program is running (again, in an idealized and simplified fashion, not specifically what DrRacket might be doing). The next chapter will focus on how a program like DrRacket might achieve those effects on its storage.
6.1 Storing primitive values
When compiling SIMP to PRIMP, our compiler/assembler uses a symbol table to translate variable names to memory locations. The symbol table may be a complicated data structure, but I show it as a simple table in the diagram below.
(vars ([i 5] [j 6]) ...)
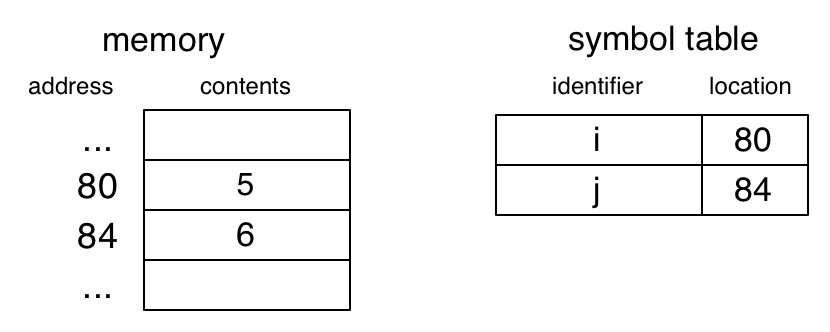
The value associated with the variable may be in a fixed location or in a stack frame. This is also done by a C compiler/assembler. This approach works due to static typing. The size of the data named by a variable is known at compile time.
For a Racket interpreter, things are not so easy. A variable may refer to data of different sizes at different points during the computation. Consequently, the compile-time symbol table is replaced by a run-time environment, mapping variables to locations. Dynamic typing means that values (stored in the heap) must be tagged with their type. Once again, I’ll represent this possibly complicated data structure as a simple table.
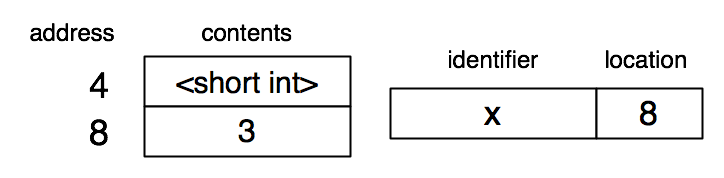
I have put the type tag in the memory word just before the value, but the entry in the symbol table points to the value and not the tag. This arrangement is common, because often the tag does not need to be accessed (and if it does, the address computation is simple).
Using this sort of diagram, I’ll go through a few short sequences of Racket expressions, and illustrate how memory might change as they are evaluated.
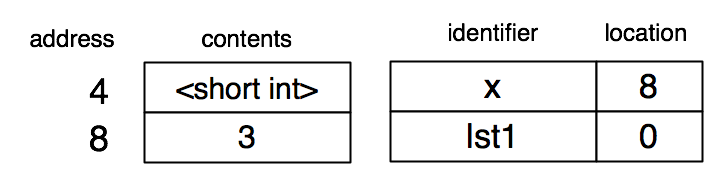
Suppose the Racket interpreter evaluates (define x 3). (For simplicity in the exposition, I’ll assume the interpreter works directly on the S-expression rather than an AST, as would be more likely in practice.) The '3 is recursively evaluated, resulting in the value 3 being placed at memory location 8, and 8 is produced as the result from the interpreter. In other words, every Racket value is represented as a pointer to a tagged value on the heap. The association of x with location 8 is added to the environment. The value of x can be unboxed, or put directly into the environment, if it can fit into less than one word, but I won’t show that here.
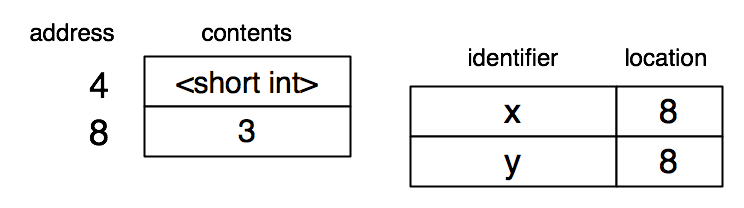
Suppose (define y x) is next. The 'x is recursively evaluated, resulting in a reference to memory location 8, which gives the binding for 'y.
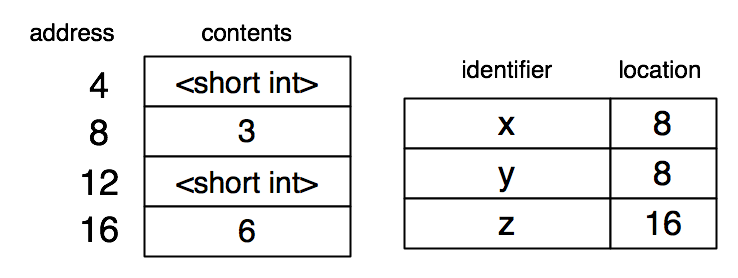
Suppose (define z (+ x y)) is next. Both 'x and 'y are recursively evaluated. These each result in a reference to memory location 8. The new value 6 is generated by adding 3 and 3. This must be put into the heap with the right type tag, and the address produced as the result of evaluating (+ x y).
Then the symbol 'z is associated with the memory address of the newly-created value.
one for the type tag;
two for pointers (memory addresses).
| (define x 3) |
| (define lst1 empty) |
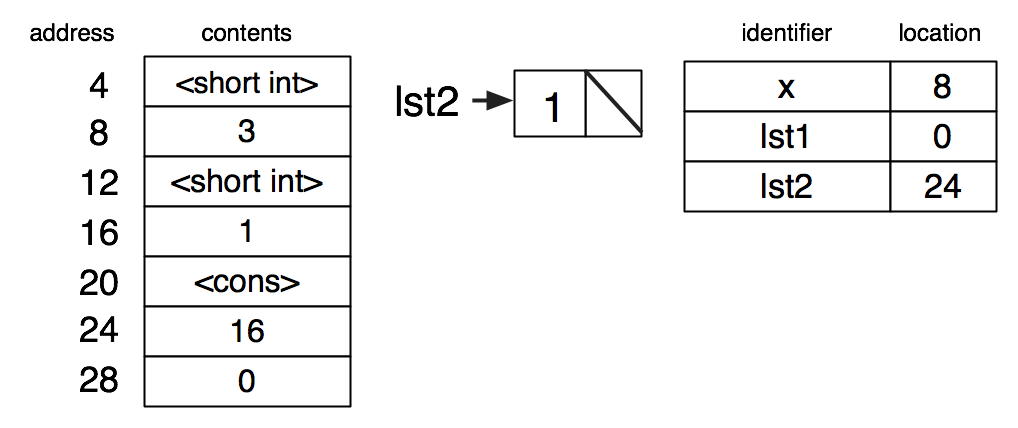
one for the type tag;
one for a pointer to the value.
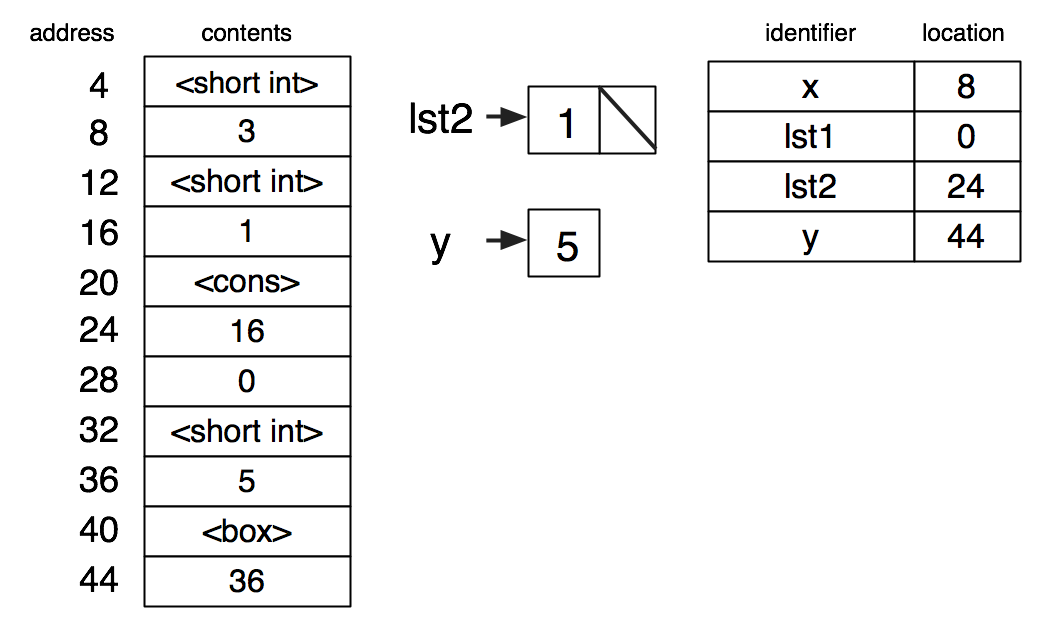
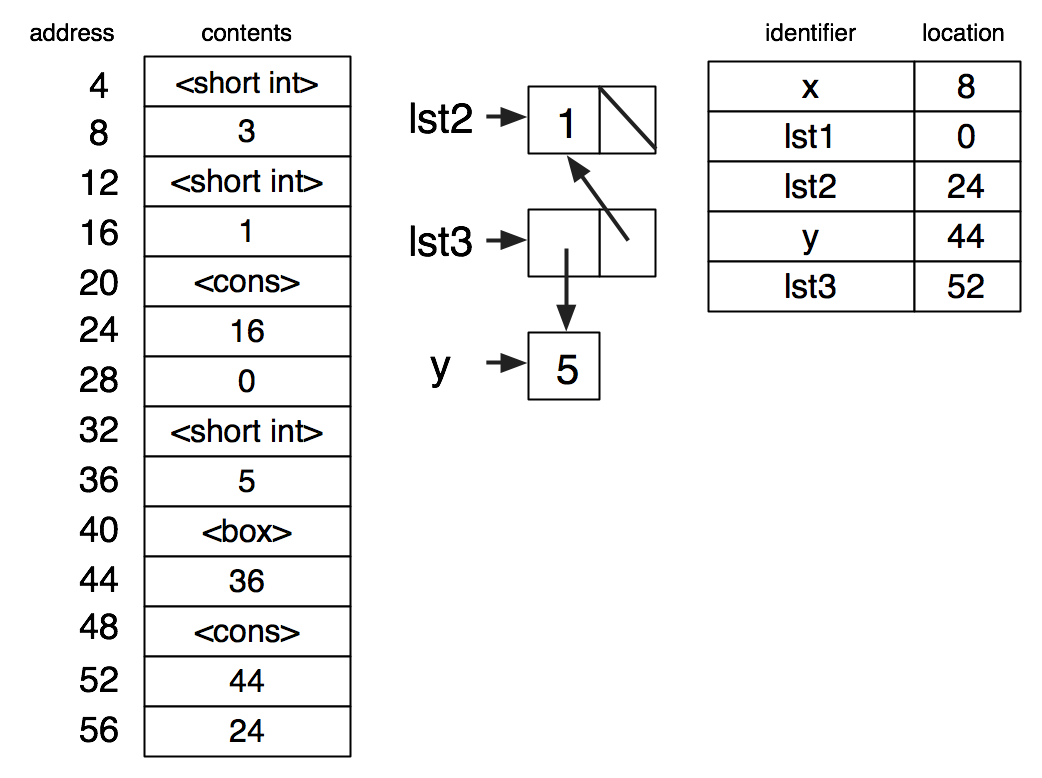
(set-box! y x)
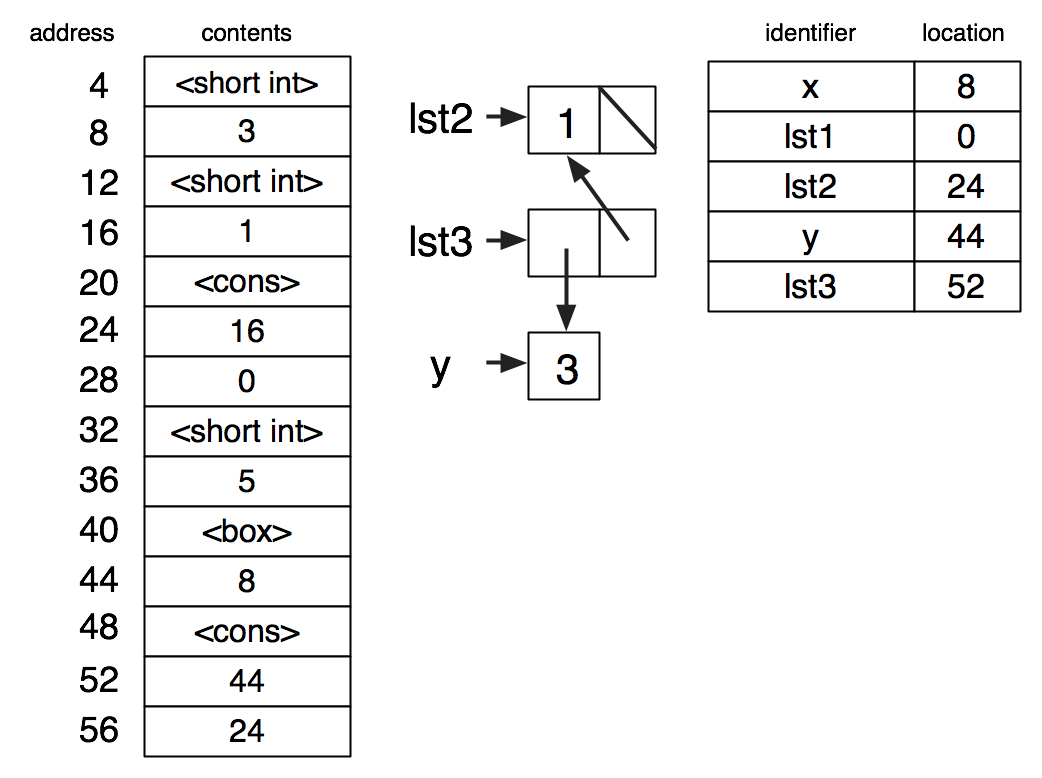
(set-box! y lst2)
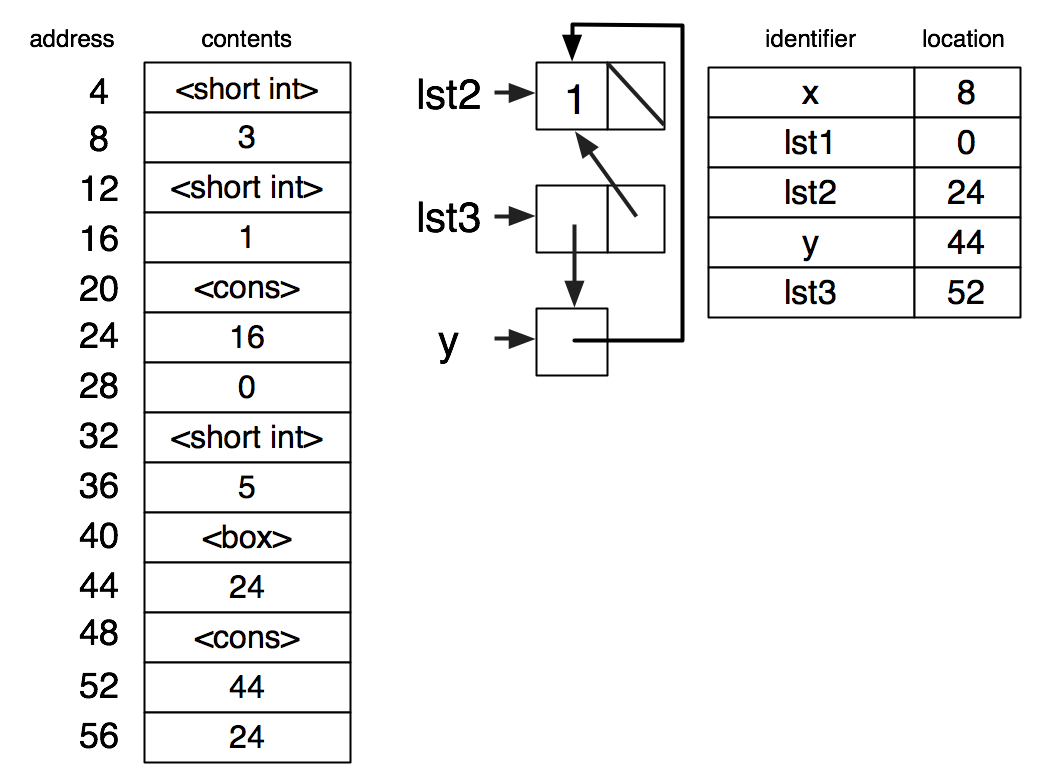
set! rebinds a name to a new value.
recursively evaluates exp;
changes the environment entry for x so that it is associated with the address of the resulting value.
(set! y x)
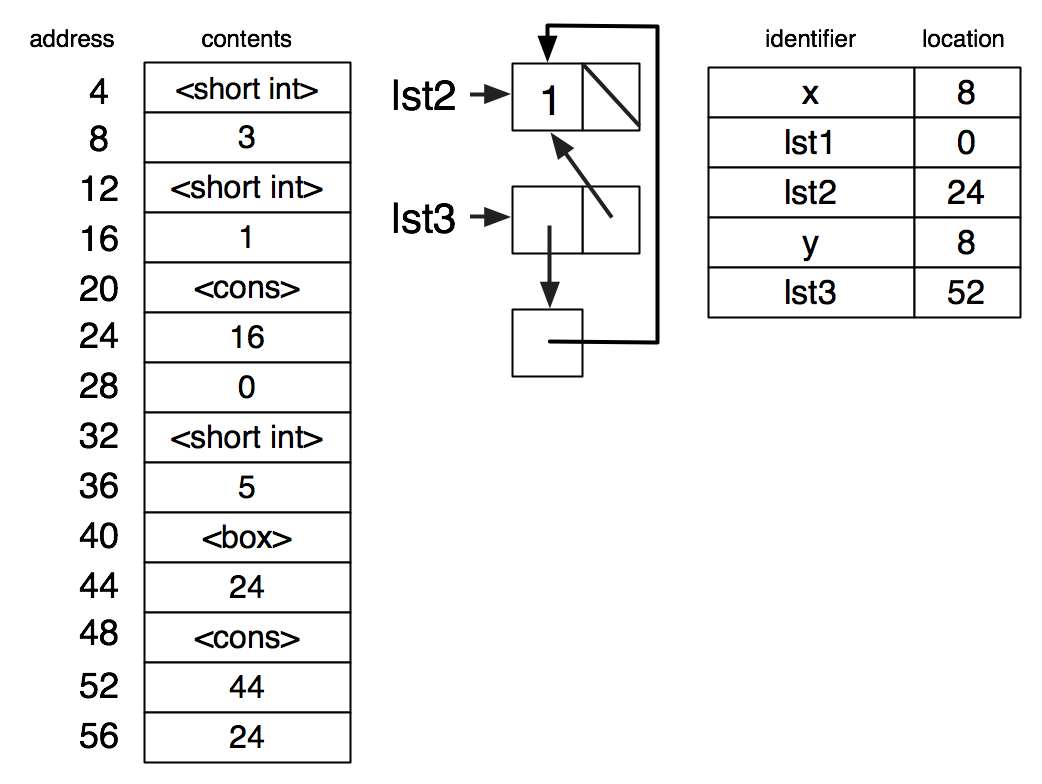
Structures generalize cons cells to a fixed number of fields, each of which is a pointer to a value.
6.2 Sharing and aliasing demystified
New cons cells (and structs), as well as values and their tags, are allocated by the interpreter from the heap. Every use of the cons primitive results in such an allocation.
In our box-and-pointer diagrams, a box represents an allocation of memory, and a pointer represents a memory address. The diagrams turn out differently than intuition from Part I would suggest, even when we consider examples that do not use mutation.
| (define (append lst1 lst2) |
| (cond |
| [(empty? lst1) lst2] |
| [ else (cons (first lst1) |
| (append (rest lst1) lst2))])) |
| (define ex1 (cons 1 (cons 2 (cons 3 empty)))) |
| (define ex2 (cons 4 (cons 5 empty))) |
| (define ans (append ex1 ex2)) |
| (append ex1 ex2) |
| => (append (cons 1 (cons 2 (cons 3 empty))) (cons 4 (cons 5 empty))) |
| => (cons 1 (append (cons 2 (cons 3 empty)) (cons 4 (cons 5 empty)))) |
| => (cons 1 (cons 2 (append (cons 3 empty) (cons 4 (cons 5 empty))))) |
| => (cons 1 (cons 2 (cons 3 (append empty (cons 4 (cons 5 empty)))))) |
| => (cons 1 (cons 2 (cons 3 (cons 4 (cons 5 empty))))) |
Here is how we might interpret this using box-and-pointer diagrams:
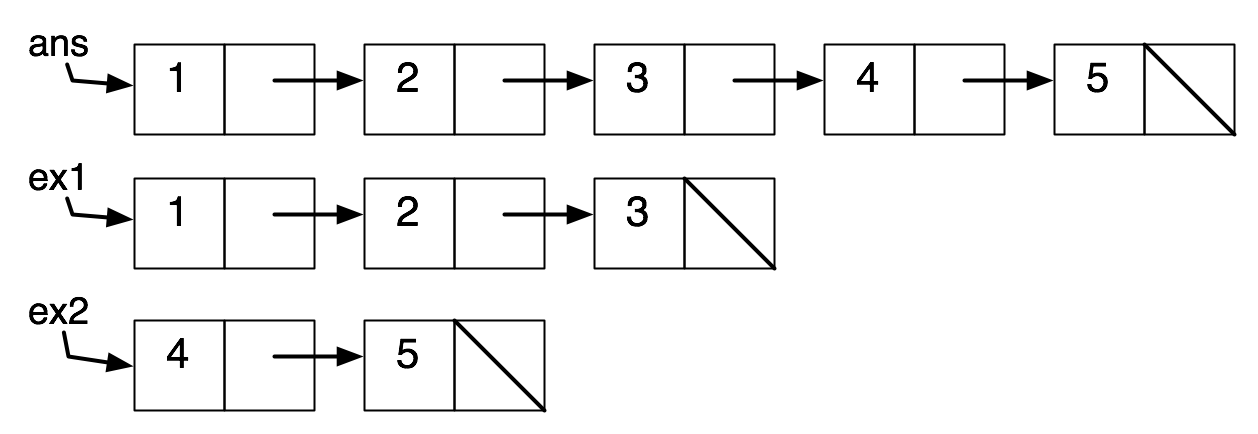
Here is how it actually looks, if we trace the computation in the memory model:
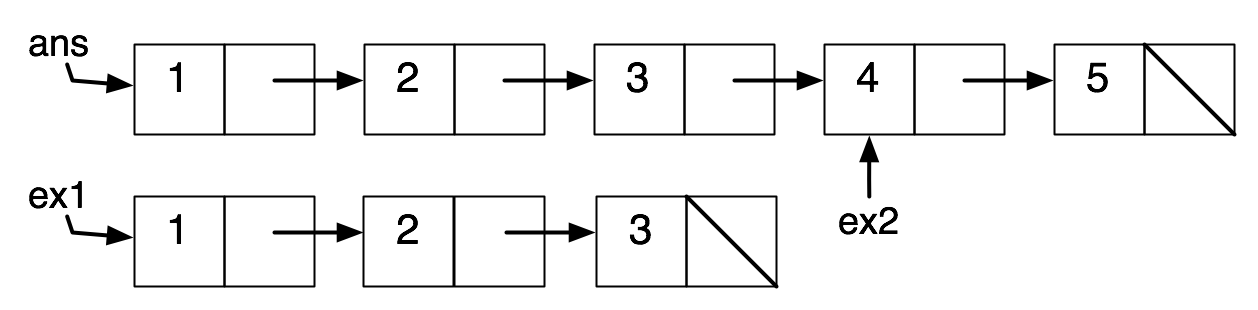
The sharing between ans and ex2 is undetectable in the absence of mutation. But we saw earlier that if (first ex2) had been a box, we could have detected the sharing.
This sharing extends to the various immutable data structures we looked at in Part I. Consider the example of adding a key-value pair to a binary search tree.
| (define (add-bst t newk newv) |
| (match t |
| ['() (make-node newk newv empty empty)] |
| [(struct node k v lft rgt) |
| (cond |
| [(= newk k) |
| (make-node k newv lft rgt)] |
| [(< newk k) |
| (make-node k v |
| (add-bst lft newk newv) rgt)] |
| [else |
| (make-node k v |
| lft (add-bst rgt newk newv))])])) |
| (define t1 (make-node 7 "A" |
| (make-node 4 "B" empty empty) |
| (make-node 12 "C" empty empty))) |
| (define t2 (add-bst t1 5 "test")) |
Here is how the result looks, before and after, using box-and-pointer diagrams to represent what happens in the memory model.
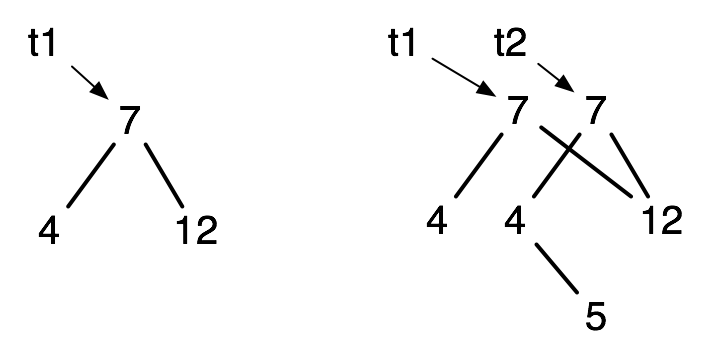
Often in imperative languages (sometimes in Racket), we may prefer to have this before and after:
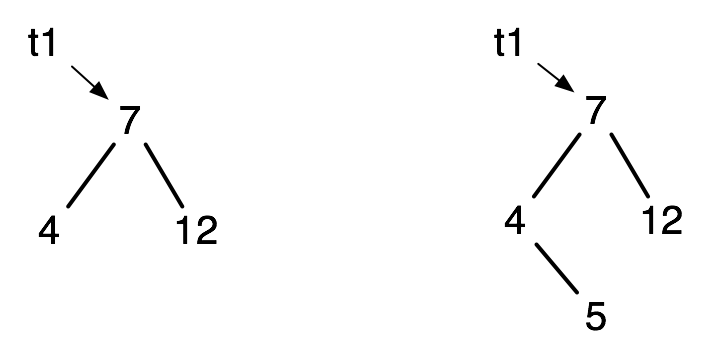
This corresponds to an implementation of the mutable Table ADT, rather than the immutable ADT of the earlier example. In this case the value of t1 does not change (it is the address of the node containing 7), but it might (for example, if t1 is empty). The solution is to have add-bst! produce the address of the new node, and to use set! in the calling code.
(set! t1 (add-bst! t1 5 "test"))
Both immutable and mutable ADTs can be used in both Scheme and C, but most treatments of data structures and algorithms tend to emphasize mutable ADTs.
It is harder to save space by sharing information;
Information about earlier state may be lost;
In concurrent situations where several programs may be modifying the same value, it is harder to ensure safety.
6.3 Managing memory
Clearly, there can be situations where some memory locations that were formerly in use are no longer pointed to by any variables or data structures in the running program. Racket (and some more recent imperative languages such as Java) incorporate automatic garbage collection, so we don’t have to worry about managing storage space. Periodically, DrRacket recovers all allocated memory no longer being used by a running program. (You can tell it is doing this because a green recycling symbol shows up in the bottom right corner.)
Memory can be reclaimed if it cannot be reached by following pointers from variables that the program is still using. This is a type of graph reachability problem that we will address later. There is an additional cost involved in memory allocation and garbage collection. This can sometimes be avoided by judicious use of mutation.
C and C++ require the programmer to explicitly manage storage space. This can be highly efficient, but also a frustrating source of errors, as you will see if you work through IYMLC.
6.4 Structural and pointer equality
We have been using the predicate equal? to test structural equality. There is a more restrictive version of equality available in Racket (and many other languages), called pointer equality.
| (define list1 (list 3 4 5)) |
| (define list2 (list 3 4 5)) |
| (define list3 list1) |
list1 and list3 point at the same list, so (eq? list1 list3) is true.
list1 and list2 point at different lists, so (eq? list1 list2) is false.
Any two of these three lists are equal in the sense of equal?.
The eq? predicate can always be computed in constant time, but this is usually not the case for equal?. However, eq? usually doesn’t do what we want.
6.5 Function application in a Racket interpreter
In the interpreters we wrote in Part I, the environment was a list of name-value bindings and thus a "stack-like" data structure.
Every function application creates a new environment frame with the name of each parameter and the corresponding memory address where the argument value can be found. This also happens for local expressions, where the environment frame contains the name of each locally-defined variable and the memory address of its value. This environment frame is removed from the symbol table when the function application or local expression is reduced to a value.
Why is the environment stack-like and not a stack? Because of functions that produce lambda values. A lambda may refer to variables in an environment frame that cannot be removed as soon as the function that produces the lambda is done with its work.
With this interpretation, we can now finally understand what our initial incorrect code for multiple address books from chapter 2 was doing (though it is still incorrect). Recall that it ran but appeared to have no effect, but our semantics could not explain this (they gave a run-time error).
| (define work '(("Arturo Belano" 6345789) |
| ("Ulises Lima" 2345789))) |
| (define home empty) |
| (define (add-entry abook name number) |
| (set! abook (cons (list name number) abook))) |
| (add-entry home "Maria Font" 2076543) |
| home => empty |
The set! mutates the binding of abook in the environment frame for the application of add-entry. This has no effect on the variable home (hence the need for boxes in order to do this properly).
6.6 Tail recursion
Tail-call optimization means replacing the current environment frame when an application in tail position is evaluated, rather than adding a new frame.
Tail recursion can be employed to reduce memory use in implementations that support tail-call optimization (such as Racket and all Scheme implementations). The following program is not tail recursive.
| (define (get-input) |
| (local ((define c (read-char))) |
| (cond |
| [(eof-object? c) empty] |
| [else (cons c (get-input))]))) |
| (get-input) |
When run on input containing \(n\) characters, this program takes linear time (roughly proportional to \(n\)) and uses a linear amount of memory for the result. But it also uses a linear amount of memory for the "stack" (sequence of environment frames).
| (define (get-input acc) |
| (local ((define c (read-char))) |
| (cond |
| [(eof-object? c) (reverse acc)] |
| [else (get-input (cons c acc))]))) |
| (get-input empty) |
This program also takes linear time and uses a linear amount of memory for the result. But it uses only constant "stack space". If we processed the characters as they are read, instead of saving them, (e.g., modifying and outputting each one), the whole program might use linear time but only a constant amount of memory.
6.7 Justifying the cost of Racket primitives
The application of most built-in functions and special forms in Racket requires constant time once their arguments are completely reduced to values by substitution. The machine language translation of primitives such as first or rest is more complicated because of the need to check type tags. The environment is also a real data structure in heap memory at run time, so even accessing variables is more complicated than with C code. I will not provide details, but intuitively it is not too hard to see how, once they are provided, we can justify our informal analyses.
Each use of cons requires the allocation and initialization of three words of memory (two for the cell, plus a tag word) from the heap. We should also take into account the cost to garbage-collect this cell (reuse its space) when nothing points to it any more. We will discuss, later in the course, the algorithms used for these tasks. An assumption of constant time per allocation and deallocation is reasonable.
Functions such as + or sqr also take constant time, assuming that short integers or inexact numbers are involved. This is also true of comparisons such as <. The assumption of constant-time arithmetic can be extended to large integers bounded by some constant (e.g. those involved in RSA encryption). If a program takes advantage of the ability of Racket to compute with unbounded integers (example: computation of Fibonacci numbers), then the length of these integers should be taken into account.
Not all primitive functions in Racket take constant time. The built-in function append, like the version we wrote earlier, takes time linear in the length of its first list argument. We analyze built-in list functions by looking at our implementations. An application of map takes time roughly proportional to the length of the list multiplied by the worst-case cost of applying the given function to one element of the list. equal? tests structural equality, which requires completely traversing both arguments in the worst case. It thus takes time proportional to the total size of its arguments.
We have seen the effects of various Racket constructs in the memory model. But we have not discussed how those effects are achieved.
6.8 Moving towards implementation in an imperative language
What are the issues to be addressed in translating what we have into an imperative language?
reading an S-expression
representing it as a data structure
avoiding deep recursion by using loops where possible
optimizing tail recursion if it exists in the interpreted program
replacing garbage collection in the Racket interpreter
garbage collection in the interpreted program if the interpreted language supports lists
Avoiding deep recursion by using loops is facilitated if our recursion is tail recursion. From the examples in earlier chapters of summing up a vector and computing Fibonacci with a loop, we can extract a recipe for converting a tail-recursive function to a loop. First, we remove the parameters, making them global "loop variables". A recursive application is replaced by mutation of these variables. Since only one variable can be mutated at a time, and its old value is destroyed, we might need to save the old value in another variable, as we did for the Fibonacci loop computation. A tail-recursive function with no parameters can be replaced by a while loop testing a Boolean "keep looping?" variable. This can be set to false in the loop for the cases where the function produces a value without further recursion.
How do we make our interpreter tail-recursive? This has benefits beyond being able to use loops. Adding support for impure features (side effects) often requires threading data through function applications.
Consider the example of rewriting a BST to have the same shape but to use consecutive natural-number keys starting at zero. Since structural recursion on a BST involves two recursive applications (on the two subtrees), it is not tail-recursive. To maintain the number to be assigned to the next node to be renumbered, we have to not only pass an initial value in to the first recursive call, but get its new value as part of the result of the first recursive call, pass that to the second recursive call, get back an even newer value, and then produce the even newer value as part of the result. It’s the same sort of threading that complicated our state-passing interpreter (in this particular example, the next number to be assigned can be considered a state variable).
With a tail-recursive function, threading data can be done just by adding another parameter, without having to complicate the result type. We can use an ad-hoc method to achieve tail recursion in our interpreter, but it might have to be rethought every time we add a feature.
Rather than demonstrate a general method directly, we will take a surprising indirect route, via the "stepper" or small-step interpreter, a version of which was an exercise in Part I.