3. Recursion Theorem

Here’s a fun puzzle:

Can you design a Turing machine \(Q\) that prints out its own encoding \(\left< Q \right>\) on the tape and then halts?

A program that prints out its own source code is known as a Quine. Here’s an example of a Quine written in Python:

s = 's = %r\nprint(s %% s)' 
print(s % s)

We will see that it is also possible to design Quines with Turing machines with the help of the Recursion Theorem. And we will see that the Recursion Theorem is also a powerful tool in establishing the limitations of Turing machines.

Building Blocks

The proof of the Recursion Theorem builds on some very simple observations.

The first simple observation is that for every string \(s\), there is a Turing machine that can add that string to the beginning of its input.

Proposition 1. For every string \(s \in \{0,1\}^*\), there exists a Turing machine \(P_s\) that on input \(x \in \{0,1\}^*\) writes the string \(sx\) on the tape and then accepts.

Proof. When \(s = a_1a_2\cdots a_n\) we can simply let \(P_s\) be the simple Turing machine that repeatedly moves left and overwrites the $n$ blank symbols to the left of \(x\) with \(a_n, \ldots, a_1\) in that order.

The machines in the proof of Proposition 1 are particularly simple. For example, the machine \(P_{01011}\) that prepends the string 01011 to the beginning of the input string is defined by this diagram:

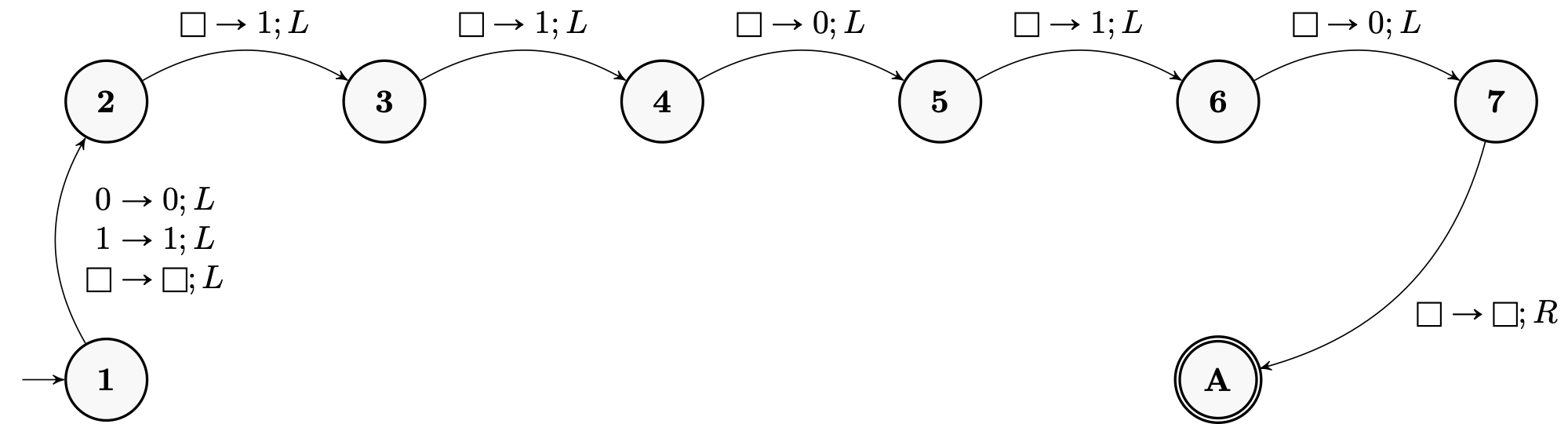
We use the simplicity of these machines to show that there is a single Turing machine that can produce the encoding of all the \(P_s\) machines.

Proposition 2. There is a Turing machine \(\textsf{FindPrinter}\) that on input \(s \in \{0,1\}^*\), replaces \(s\) with \(\left< P_s \right>\) on the tape then accepts.

Proof. Given \(s\) as input, it is straightforward to determine the transition function for the corresponding Turing machine \(P_s\) as defined above. We can then write its encoding on the tape.

The concatenation of two Turing machines \(A\) and \(B\) is the machine that we represent with \(AB\) that on input \(x\) first simulates \(A\) on \(x\), then simulates \(B\) on the input left on the tape after \(A\)’s simulation, and finally accepts if and only if \(B\) accepts.

Note that the encoding of the concatenated machine \(AB\) is not equivalent to the concatenation of the encodings of \(A\) and \(B\). Nonetheless, our third simple observation is that there is a Turing machine that, given the encoding of any two Turing machines, can produce the encoding of their concatenation.

Proposition 3. There is a Turing machine \(\textsf{Concat}\) that on input \(\left<A\right> \left<B\right>\) for any two Turing machines \(A\) and \(B\), replaces that input with \(\left< AB \right>\) on the tape and then accepts.

Proof. The Turing machine \(AB\) has the same initial state as \(A\). When \(A\) halts, the machine \(AB\) instead transitions to the initial state of \(B\). And then when \(B\), halts, \(AB\) does so and accepts if and only if \(B\) did. Therefore, the transition function for \(AB\) is easy to determine when we have the transition functions for both \(A\) and \(B\), and we can easily encode it to generate the desired output.

The Recursion Theorem

We’re now ready to prove the Recursion Theorem.

Recursion Theorem. For every Turing machine \(M\), there exists a Turing machine \(Q_M\) that on every input \(x \in \{0,1\}^*\) simulates \(M\) on the input \(\left< Q_M \right> x\).

Proof. First, we claim that there is a Turing machine \(R\) that on input \(\left< N \right> x\) for any Turing machine \(N\) and any binary string \(x\) replaces that input with the string

\[\left< P_{\left< N \right>} N \right> x\]

on the tape and then halts. There exists such an \(R\) because of the simple observations we established above: First, we can run \(\textsf{FindPrinter}\) on \(\left< N \right>\) to obtain \(\left< P_{\left< N \right>} \right>\). Then, we can run \(\textsf{Concat}\) on the input \(\left< P_{\left< N\right>} \right> \left<N\right>\) to obtain \(\left< P_{\left<N\right>} N \right>\). Keeping the original input \(x\) to the right of this string gives us the desired output.

Note that the definition of \(R\) does not depend on \(M\).

Define \(Q_M\) to be the Turing machine

\[Q_M = P_{\left< RM \right>} RM.\]

When we run \(Q_M\) on the input \(x\), we obtain

\[x \stackrel{P_{\left< RM \right>}}{\to} \left<RM\right>x \stackrel{R}{\to} \left<P_{\left<RM\right>} RM \right> x = \left< Q_M \right> x \stackrel{M}{\to} M( \left<Q_M\right>x )\]

where we write \(M( \left<Q_M\right> x)\) to denote the output of \(M\) on input \(\left<Q_M\right>x\).

We can use the Recursion Theorem to prove the existence of a Turing machine that prints out its own encoding.

Corollary. There is a Turing machine \(Q\) that on input \(\varepsilon\) prints out \(\left< Q \right>\) on the tape and then halts.

Proof. Let \(T\) be the trivial Turing machine that does nothing: it simply leaves the original input on the tape and immediately accepts. By the Recursion Theorem, the machine \(Q_T\) on input \(\varepsilon\) simulates \(T\) on the input \(\left< Q_T \right>\), so it accepts with its own description on the tape.

Application to Undecidability

The Recursion Theorem also has far-reaching consequences for proving undecidability results. The power of the theorem is perhaps best encapsulated by the informal observation that

Every Turing machine can obtain its own description.

Let’s state this observation slightly more precisely.

Corollary. Without loss of generality, we can always assume that a Turing machine has access to its encoding as well as its usual input \(x\) on the tape.

Proof. If we want a Turing machine to access its own description, let us first design a Turing machine \(M\) that takes inputs of the form \(\left< N \right> x\) for any Turing machine \(N\) and then is designed under the assumption that \(\left< N \right>\) is its own description.

Of course, the problem with the construction above is that \(\left< N \right>\) is certainly not necessarily the encoding of \(M\) itself; it could be of any other Turing machine. But consider now the machine \(Q_M\) promised to exist by the Recursion Theorem. On input \(x\), \(Q_M\) simulates \(M\) on the input \(\left< Q_M \right> x\) so that it does have access to its own description during execution.

We can use this corollary to obtain short proofs of many undecidability results. Here is one typical example:

Theorem 4. The language

\[A_{TM} = \{ \left< M \right>x : M \mbox{ accepts } x \}\]

is undecidable.

Proof. Assume on the contrary that \(A_{TM}\) is decidable by the Turing machine \(T\). Consider the machine \(M\) that on input \(x\) does the following:

1. Obtain its own encoding \(\left< M\right>\) using the Recursion Theorem.
2. Run \(T\) on input \(\left< M \right> x\).
3. Do the opposite of \(T\): reject if \(T\) accepts, and accept if \(T\) rejects.

By construction, \(M\) accepts \(x\) if and only if \(T\) does not accept \(\left< M \right> x\). But this contradicts the claim that \(T\) decides \(A_{TM}\).

Relation to Diagonalization

Theorem 4 can also be proved directly using a diagonalization argument:

Alternate Proof of Theorem 4. Assume on the contrary that \(A_{TM}\) is decidable by the Turing machine \(T\).

The set of Turing machines is countable and so is the set of the encodings. Consider then the infinite table whose rows are labelled with the Turing machines in some order \(M_1,M_2,M_3,\ldots\) and the columns are labelled with their encodings \(\left< M_1 \right>, \left< M_2 \right>, \left< M_3 \right>, \ldots\). Label the cell \((M_i, \left< M_j \right>)\) with a 1 if \(M_i\) accepts the input \(\left< M_j \right>\) and with a 0 otherwise. The table looks like this:

	\(\left< M_1 \right>\)	\(\left< M_2 \right>\)	\(\left< M_3 \right>\)	\(\cdots\)
\(M_1\)	0	0	0	\(\cdots\)
\(M_2\)	1	0	0	\(\cdots\)
\(M_3\)	0	1	1	\(\cdots\)
\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\vdots\)	\(\ddots\)

Define now the Turing machine \(D\) that takes in as input the encoding \(\left< M \right>\) of a Turing machine \(M\), runs \(T\) on the input \(\left< M \right> \left< M \right>\), and accepts if and only if \(T\) rejects.

By construction, \(D\) accepts \(\left< M \right>\) if and only if \(M\) does not accept its own encoding \(\left< M \right>\). Or, in other words, it accepts \(\left< M_i \right>\) if and only if the diagonal entry \((M_i, \left< M_i \right>)\) is 0.

Since the table includes all Turing machines, it includes \(D\) and so \(D = M_k\) for some index \(k\). But then what is the entry of the table at the cell \((D, \left< D \right>) = (M_k \left< M_k \right>)\)? Since \(D\) accepts \(\left< D \right> = \left< M_k \right>\) if and only if \(M_k = D\) does not accept \(\left< M_k \right>\), it is impossible to define a value in this cell without obtaining a contradiction.

The two proofs are conceptually similar, though the proof using the Recursion Theorem is quite a bit shorter. Indeed, we can think of the Recursion Theorem as giving us “diagonalization in a box”. As we will see in the next lecture, it can be used to prove many other undecidability results as well.

Eric Blais ©2024 — Last edited on Jan. 14, 2024