13. P vs. BPP

How much power does randomness add to computers? We can examine this question by determining how the class \(\mathbf{BPP}\) fits in with the other existing complexity classes that we have studied previously.

BPP and polynomial-size circuits

As we have seen earlier, families of polynomial-size circuits can compute every language in \(\mathbf{P}\). They can also compute every language in \(\mathbf{BPP}\).

Theorem. (Adleman) \(\mathbf{BPP} \subseteq \mathbf{P/poly}\).

Proof. Fix any language \(L \in \mathbf{BPP}\). By the success amplification theorem from the last lecture, there exists a polynomial-time probabilistic Turing machine \(A\) that \(2^{-(n+1)}\)-decides the language \(L\). (In other words, for every input \(x\) of length \(n\), \(A\) correctly determines whether \(x \in L\) except with probability at most \(2^{-n}/2\).)

Fix any \(n \in \mathbb{N}\). Let \(m = \ell(n)\) be the length of the random strings used by \(A\) on inputs of length \(n\). We will say that a random string \(r \in \{0,1\}^m\) is bad for input \(x \in \{0,1\}^n\) if \(A\) does not correctly accept or reject \((x,r)\).

For any fixed \(x \in \{0,1\}^n\), the correctness guarantee on \(A\) implies that there are at most \(2^{m}/2^{n+1}\) random strings \(r \in \{0,1\}^m\) that are bad for \(x\). But this means that there can be at most \(2^n \cdot 2^m/2^{n+1} = 2^m/2\) random strings \(r \in \{0,1\}^m\) that are bad for any input of length \(n\). Therefore, for at least half of the random strings, \(A\) correctly accepts or rejects every \(x \in \{0,1\}^n\). We can then design a polynomial-time Turing machine with advice that correctly decides \(L\) by choosing one of the good random strings to be the advice string \(a_n\) and then simulating \(A\) with this advice string in place of the random string.

BPP and the Polynomial Hierarchy

We can also use the success amplification theorem to place \(\mathbf{BPP}\) in the second level of the polynomial hierarchy.

The proof of that result uses two basic combinatorial lemmas. For a set \(S \subseteq \{0,1\}^m\) and a vector \(u \in \{0,1\}^m\), define the shift of \(S\) by \(u\) to be the set

where \(x \oplus y = (x_1 \oplus y_1, \ldots, x_m \oplus y_m)\) is the bitwise XOR of the two vectors.

The first combinatorial lemma states that when \(S\) is small, the union of a few shifts of \(S\) does not cover all of \(\{0,1\}^m\).

Lemma 1. Fix any \(n \ge 1\) and \(m\) in the range \(n < m < 2^n\). For any \(S \subseteq \{0,1\}^m\) of cardinality \(|S| \le 2^{m-n}\) and any set of \(k = \lceil \frac mn \rceil\) vectors \(u_1,\ldots,u_k \in \{0,1\}^m\), we have

\[\bigcup_{i=1}^k (S \oplus u_i) \neq \{0,1\}^m.\]

Proof. For every vector \(u \in \{0,1\}^m\), \(|S \oplus u| = |S| \le 2^{m-n}\). So by the union bound,

\[\left| \bigcup_{i=1}^k (S \oplus u_i) \right| \le k |S| \le k \frac{2^m}{2^n} = \frac{k}{2^n} 2^m.\]

This cardinality is strictly less than \(2^m\) when \(k < 2^n\).

The second combinatorial lemma shows that when a set is large, it is always possible to cover all of \(\{0,1\}^m\) with a few shifts of that set.

Lemma 2. Fix any \(n \ge 1\) and any \(m \ge n\). For any \(S \subseteq \{0,1\}^m\) of cardinality \(|S| \ge (1 - 2^{-n})2^m\), there exist \(k = \lceil \frac m n \rceil + 1\) vectors \(u_1,\ldots,u_k \in \{0,1\}^m\) such that \(\bigcup_{i=1}^k (S \oplus u_i) = \{0,1\}^m\).

Proof. Consider what happens when we draw \(u_1,\ldots,u_k\) uniformly and independently at random from \(\{0,1\}^m\). For any fixed \(r \in \{0,1\}^m\), the events \(r \notin (S \oplus u_i)\) are independent and so

\[\Pr[ r \notin \bigcup_{i=1}^k (S \oplus u_i)] = (2^{-n})^k = 2^{-nk}.\]

Therefore, by a union bound argument over all \(r \in \{0,1\}^m\), the probability that there exists some string in \(\{0,1\}^m\) that is not included in \(\bigcup_{i=1}^k (S \oplus u_i)\) is at most \(2^m \cdot 2^{-nk} = 2^{m - nk}\). From our choice of \(k\), this probability is at most \(\frac12\). This means that there must exist at least one choice of \(u_1,\ldots,u_k\) for which \(\bigcup_{i=1}^k (S \oplus u_i) = \{0,1\}^m\). (In fact, it means that there are many such vectors with this property, but we only need that there is at least one for this proof!)

We are now ready to place \(\mathbf{BPP}\) in the polynomial hierarchy.

Theorem. \(\mathbf{BPP} \subseteq \mathbf{\Sigma_2} \cap \mathbf{\Pi_2}.\)

Proof. Let’s show that \(\mathbf{BPP} \subseteq \mathbf{\Sigma_2}\). Fix any language \(L \in \mathbf{BPP}\). By the Success Amplification Theorem, there exists a polynomial-time probabilistic Turing machine \(M\) that \(2^{-n}\)-decides \(L\). For any \(x \in \{0,1\}^n\) and set \(m = \ell(n)\). Let \(S_x \subseteq \{0,1\}^{m}\) denote the set of random strings \(r\) for which \(M\) accepts \((x,r)\). The correctness guarantees of \(M\) imply that

• When \(x \in L\), then \(|S_x| \ge (1-2^{-n}) 2^m\).
• And when \(x \notin L\), then \(|S_x| \le 2^{-n} \cdot 2^m\).

By Lemmas 1 and 2, we get that \(x \in L\) if and only if there exist \(u_1,\ldots,u_k \in \{0,1\}^m\) for which every \(r \in \{0,1\}^m\) satisfies \(r \in \bigcup_{i=1}^k (S_x \oplus u_i)\). But by definition, \(r \in \bigcup_{i=1}^k (S_x \oplus u_i)\) if and only if \(M\) accepts \((x,r \oplus u_i)\) for at least one index \(i \in 1,2,\ldots,k\).

Since the check that \(M\) accepts at least one pair \((x, r \oplus u_i)\) can be performed in polynomial time, this means that we have obtained a polynomial-time \(\Sigma_2\)-verifier for \(L\).

The proof that \(L \in \mathbf{\Pi_2}\) is obtained by symmetry of \(\mathbf{BPP}\): when \(L \in \mathbf{BPP}\), then so is \(\overline{L} \in \mathbf{BPP}\) as well. And by the argument above, this means that \(\overline{L} \in \mathbf{\Sigma_2}\), which means that \(L \in \mathbf{\Pi_2}\).

Polynomial Identity Testing

What about \(\mathbf{P}\) vs. \(\mathbf{BPP}\)? Can we show that the two classes are identical? Or that they are different? The key to doing so appears to be the study of the polynomial identity testing (PIT) problem.

A (multivariate) polynomial is an expression that involves constants and variables multiplied and added together, as in this example:

How many addition and multiplication operations do we need to evaluate a given polynomial? We can evaluate the polynomial \(p(x,y)\) above in the naïve way with a total of 23 multiplications and additions, by computing

But we can also do better by observing that the polynomial \(p(x,y)\) can also be expressed as

This polynomial only requires 4 operations to compute: use a multiplication and an addition to obtain \(3x + y\). Then by multiplying this result with itself, we obtain \((3x + y)^2\), and one more multiplication applied to this result with itself gives us the final polynomial \((3x+y)^4\).

Any strategy for evaluating polynomials can be expressed as an arithmetic circuit, whose inputs are constants or variables, and whose gates are addition or multiplication gates. For example, an arithmetic circuit for the polynomial \(5x + 6xy^2 + z\) is

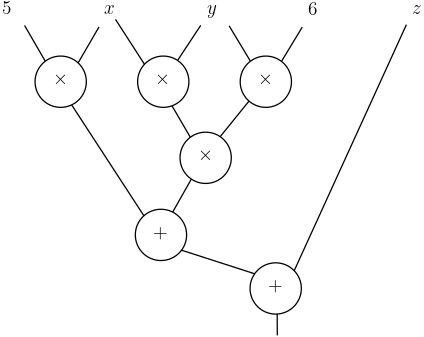
These arithmetic circuits bring up a fundamental question: given two arithmetic circuits, can we efficiently determine if they represent the same polynomial? This question is equivalent to one that seems even simpler: given an arithmetic circuit \(C\), can we determine if it is equivalent to the zero polynomial \(p(x_1,x_2,\ldots,x_n) = 0\)? And that question can be answered by studying the complexity of the language

The language \(\textsf{PIT}\) can be computed in polynomial time with randomized algorithms.

Theorem. \(\textsf{PIT} \in \mathbf{BPP}\).

But, as of now, we do not know if it is possible to decide \(\textsf{PIT}\) in polynomial time with deterministic algorithms. This is one of the main open problems in complexity theory today, and a great entry point to the study of randomized algorithms and derandomization.

Eric Blais ©2024 — Last edited on Mar. 4, 2024