2 Introduction to C
This chapter provides an introduction to the programming language C. C provides thin abstractions over assembly language, and many features of the language are best understood by thinking about similar tasks carried out by sequences of machine instructions in a model that more closely resembles a physical electronic computer (as opposed to the more abstract computational model based on program rewriting typically used to explain Racket).
C has sometimes been called the "portable assembler", because while its closeness to the machine level means it can behave differently from machine to machine, it is also possible, with some care, to write code in C that can easily be transferred from one machine architecture to another. In this phrase "assembler" is a common term for human-readable (and writeable) representation of machine-language instructions. FICS explores that idea in more depth.
Learning C can be a much more frustrating experience than learning Racket, because the language is much more low-level, and does less for the beginning programmer. This is compounded by the fact that the software tools are designed for professionals. Despite the popularity of C, there is no software for assisting the C programmer that even comes close to the user-friendliness of DrRacket. People have occasionally tried to build such tools, but these efforts tend to be abandoned after a few years.
Consequently, it is even more important to pay attention to ideas that show up in the study of Racket: the computational model, and proper design and testing. You can learn the hard way, by neglecting these, or you can make your life easier by keeping them in mind, and understanding carefully what you are about to try doing, structuring your program so that you can get useful information out of it in the event that it does not work perfectly the first time.
These notes differ from conventional introductions to C, such as the ones provided by the optional textbooks, in that they attempt to build on the knowledge gained from studying Racket. As a result, topics are covered in a different order from those (and other) books. There are suggested reading schedules in the previous chapter.
What follows assumes that you have chosen a CLE and editor as described in the previous chapter, and have practiced with both. If not, go back and do that first.
2.1 Basics
I use the following simple model of memory in FICS. While more accurate than what is discussed in a typical course (including the aforementioned CS 136) or the textbooks, it is still idealized in some respects. It omits many details, but includes enough to be accurate about the uses of C here.

In this memory model, memory is grouped into 32-bit words comprised of four 8-bit bytes, and each byte has an address which is a natural number (that can be represented with 32 bits). A word can be considered to have the same address as its lowest byte, and location 0 is considered special and thus removed from the diagram. (Historical note: 64-bit architectures are universal now, and mostly were when this material was developed. A 64-bit word has eight 8-bit bytes. But for the kinds of programming done here, this distinction can be ignored, and using 32 bits makes examples more readable.)
Memory contains both program and data. A machine-language instruction fits into a word or sequence of words. To run an assembly-language program (assembly language is a human-readable representation of machine language) we first use an assembler to convert the program to machine code. We then load the machine-language program into memory and run it.
The process is similar with C. We use the C compiler to convert a C program to an executable, which is machine code in a format that the operating system can use to load and run the program. We then proceed to instruct the operating system to do that. Both of these two steps are done via commands typed into a shell window.
Here is the standard first program in C.
#include <stdio.h> |
|
int main(void) { |
printf("Hello, world!\n"); |
return 0; |
} |
It does the same thing as the following program in Racket. So does the single Racket string "Hello, world!", which is a legal Racket program, but the more elaborate version below serves as a useful standard of comparison.
| (define (main) |
| (begin |
| (printf "Hello, world!\n") |
| 0)) |
| (main) |
Let’s dissect the C program. It starts with this line:
#include <stdio.h> |
This is actually a directive to the C preprocessor, which does simple rewriting of programs before compilation. In this case, information about standard I/O functions (from a library) is provided to the compiler while compiling the program. The file extension .h is typical for a header file providing such information. Soon we will be writing our own header files.
This statement:
int main(void) |
starts the beginning of the main function in the program. Every complete C program must have a main function, which is automatically called when the program is run. Note, however, that C programs may be split among several files, and only one file should have such a function.
In this case, the function has no parameters, though later on we will see that some parameters may be specified. The type of the result is specified, and for main, this must be int (for integer).
If a function has parameters, the type of each parameter must also be specified.
The following expression represents the application of a function to an argument.
printf("Hello, world!\n") |
Note that the function name is outside the parentheses. If there is more than one argument, the arguments are separated by parentheses. We can make this expression into a statement by putting a semicolon after it. A statement produces no value; it is executed for its side effects.
printf("Hello, world!\n"); |
You can also think of this statement as producing the value void, in a manner similar to the Racket printf function producing the value #<void>, though the semantics of Racket and C are somewhat different. A Racket program has no statements, but it does have some expressions that produce #<void> . A C program typically has many statements, some of which are formed from expressions by adding a semi-colon at the end.
Here is a block consisting of two statements.
{ |
printf("Hello, world!\n"); |
return 0; |
} |
The block is formed by curly braces, within which there is a sequence of statements. This resembles a begin expression in Racket. The second statement in the block:
return 0; |
shows a typical way of returning a result from a function (the C equivalent of a Racket function application producing a value), with an explicit return statement. Where is the result returned to, in this case? To the calling program (typically the shell), where it can be used to indicate conditions such as success or failure. We will not be using this feature here, and will always return zero.
Here, then, is the complete main function, consisting of a header declaring the name of the function and parameters, types of parameters and return value, and a statement or block for the body of the function.
int main(void) { |
printf("Hello, world!\n"); |
return 0; |
} |
Notice the different style of indentation compared to Racket, and the placement of curly braces. There are many different styles in writing C, but the style I are using is quite common, and I recommend it. If you choose to write in a different style, at least do so consistently, so that people can learn how to read your programs.
Here is the complete program again.
#include <stdio.h> |
|
int main(void) { |
printf("Hello, world!\n"); |
return 0; |
} |
We can type this program into a text editor and save it into a file, perhaps called hello.c. The .c file extension is a good idea, as it provides information to the compiler.
To compile and link the program (I will explain linking shortly), the following shell command works.
clang -o hello hello.c
This invokes clang, the C compiler. The dashes precede various flags or directives to the compiler. -o specifies the output file, which in this case is hello.
There are other C compilers, and you may choose to use one of them – for example, the gcc compiler, which is widely used (though it has more confusing error messages).
The effect of this command is to create the executable file hello. To run this file, simply type ./hello (or ./hello.exe on Windows). The ./ is a small trick to get around the fact that the current directory is not searched for commands, in case you have files called ls or with the same name as other commands. The dot . indicates the current directory, so this is explicitly saying that you have an executable file in the current directory. As with running a Racket program on the command line, the output appears in the window, and can be redirected to a file using the redirection features of the shell. (Input also works in a similar fashion, even though this program doesn’t do any.)
Here’s how we add comments to C programs.
/* This is a |
multi-line comment */ |
|
// This is a single-line comment (C99) |
|
#include <stdio.h> |
|
int main(void) { |
printf("To C, or not to C: "); // Roll over, |
printf("that is the question.\n"); // Shakespeare |
return 0; |
} |
In general, C programs have to be commented more than Racket programs. I won’t always do so here, for brevity, but you should develop the habit.
The following program illustrates the definition and use of variables.
#include <stdio.h> |
int main(void) { |
int i = 5; |
int j; |
j = i + 1; |
printf("%d\n", j); |
return 0; |
} |
As before, let’s examine some statements within this program.
int i = 5; |
This statement declares the local variable i and initializes its value to 5. It is comparable to this Racket expression:
(define i 5)
In the memory model, a variable is stored in a word of memory, though in practice the code generated by the compiler may assign frequently-used variables to registers (a processor typically has a small set of registers, each holding a word; access to these is faster than to the larger memory).
This statement is similar, but lacks initialization.
int j; |
The variable will have a value, but the value cannot be predicted at compile time. (It’s the value left in memory or the register by earlier code.) Using the value of an uninitialized variable (before it is explicitly set by the program) does not cause a run-time error right away, but it may cause your program to behave unexpectedly.
j = i + 1; |
This is an assignment statement.
It resembles the Racket expression
(set! j (+ i 1)).
However, there are some differences.
The value produced by the Racket expression is #<void>;
however, in C, the value of an assignment expression
is the value of the right-hand side, permitting
statements like k = j = i + 1;.
In fact, the statement j = i + 1;
is actually closer to
(set-box! jbox (+ (unbox ibox) 1))
in that the left-hand side of an assignment can be an expression, rather
than simply an identifier. We will see ways of computing such expressions
soon.
Note also that + is an infix operator in C. There are many infix operators, which have levels of precedence. The expression i + j * k is computed as i + (j * k), since * has higher precedence than +. In order to read code that avoids parentheses, one must be aware of relative precedence. Most textbooks and reference books will have a table of operator precedence somewhere, and you can probably find one on the Web if you need it.
printf("%d\n", j); |
Here we see how multiple arguments to a function are handled, by separating them with commas. We also see that the format string for C’s printf has a different specification than in Racket. %d is the format escape for decimal numbers. For a more complete list of format escapes, see the C textbooks, or an online resource.
2.2 Types
Racket has dynamic typing. Every value in Racket has a type. An identifier in a program may be bound to values of different types at run time.
C has static typing. Every expression in C must have a type that can be determined at compile time.
Racket is type-safe. Performing an operation on a value that is not of the right type leads to a run-time error.
C is not type-safe. No run-time checking is done, and much of the compile-time checking can be circumvented. Types in C are more an aid to effective compilation than a way to guard the programmer against error.
The int type is a 32-bit two’s-complement integer (range \(-2,147,483,648\) to \(2,147,483,647\)). [Two’s complement representation is discussed in FICS.] Overflow in arithmetic operations does not cause a run-time error (typically the lower 32 bits of the result are kept).
The float (floating point) type approximates a real number by a rational number stored in a certain format (the denominator will be a power of 2; floating point numbers are identical to Racket’s inexact numbers). We will not be using these much (if at all) here.
The char type uses only 8 bits, and is typically treated as a small integer. ’a’ and ’\n’ are C character constants. The function getchar (similar to readchar in Racket) produces an int, not a char. The reason for this is that each of the 256 possible 8-bit patterns represents a legal character. But getchar needs to signal end of file, also. (It uses the constant EOF, defined by including stdio.h).
The following program demonstrates more features of the language.
int gcd(int n, int m) { |
if (m == 0) { |
return n; |
} else { |
return gcd(m, n % m); |
} |
} |
|
int main(void) { |
int i = 245; |
int j = 135; |
printf("GCD(%d,%d) is %d\n", i, j, gcd(i,j)); |
return 0; |
} |
Once again, we examine some statements within the program.
int gcd(int n, int m) { |
This is an example of the syntax in declaring a function with multiple parameters. The type of each parameter is specified, and parameters are separated by commas.
We see two new operators in the program. % is the infix remainder operator. == is the infix equality operator, which is not as general as Racket’s equal, but applies to more types than Racket’s =. What type does == produce?
There is no real Boolean type in C. == produces an integer value, 0 or 1.
if (m == 0) { |
return n; |
} else { |
return gcd(m, n % m); |
} |
0 fails the if test, everything else passes. Suppose we had forgotten to type the second equal sign in ==, and typed if (m = 0) instead. [This is a common error, even among experienced programmers, cough cough.] The expression inside the parentheses is an assignment, which sets the value of m to 0, and has the value 0. So the test will always fail. [In this case, we would get a divide-by-zero error in computing n % m].
To somewhat remedy this, the C99 standard provides the type bool defined in stdbool.h, which defines constants true and false. But this just makes programs more readable. It does not avoid the error described above.
The if statement in C does not produce a value (unlike the if construct in Racket). It gets work done through side effects. The code to be executed if the test expression is nonzero (and similarly if it is zero) can be a single statement or a block, and because no value is produced, the else part is optional. The other comparison operators are also infix. The equivalent of Racket’s or is the infix operator ||, of and is infix &&, and of not is the prefix operator !.
In a Racket program, we can put the functions in any order. But compilation in C is typically top-down, one-pass. If we put the code for gcd after the code for main, it will not compile without warnings. They will be warnings, not errors, because the compiler will make assumptions about the types of parameters and result of gcd while compiling main. It is generally not a good idea to rely on such assumptions.
The fix, both to make the compiler happy and to improve readability, is to add a prototype before main. This is a statement like the following:
int gcd(int n, int m);
It just specifies the types of parameters and result to avoid assumptions. Prototypes will be an important tool in splitting a C program into multiple files (as we’ll discuss shortly).
2.3 Separate compilation
Testing C code is more complicated than testing a Racket program, because expressions at the top level are not evaluated and printed, because there is no REPL (read-evaluate-print loop, like Racket’s Interactions window), and because mutation and I/O are pervasive.
Here is one way to do simple testing, which turns out to be too simple in general, but will suffice to provide a main function for our gcd function.
#include <assert.h> |
|
int main(void) { |
assert(gcd(135,245) == 5); |
assert(gcd(37,49) == 1); |
assert(gcd(12,24) == 1); /* don't do this! */ |
assert(gcd(2,4) == 2); |
return 0; |
} |
The effect of assert is to do nothing if the test inside passes, and to report an error if the test fails. Thus you should not write a test that you know will fail (like the one above), as it means the rest of the tests will not be executed. We only included the bad test above so that you could compile and run the code to see what happens when a test fails.
This is much too simple a mechanism to be of much use even for beginners. I will discuss more useful methods in the section on testing.
We now turn to the topic of program organization in separate files (possibly with separate compilation). This is treated fairly late in the King C textbook, and it is premature to read those chapters now, but a cursory overview of the subject will let us set up an effective framework for development and testing of programs.
The GCD example from above is too short a program to really break up into separate files, but we will do so anyway, as a simple illustration of the technique. Here is one possible method of organization.
|
int gcd(int n, int m) { |
/* definition of function */ |
} |
|
int my_global_variable; |
int gcd(int n, int m); |
|
extern int my_global_variable; |
#include <stdio.h> // found in standard library location |
#include "gcd.h" // in same directory as gcd-driver.c |
|
int main() { |
/* driver program */ |
} |
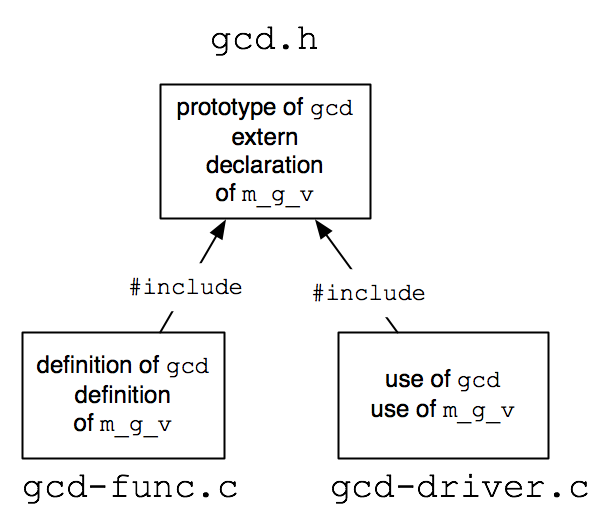
Having split the program up, we now need to discuss compilation and linking of separate files. For this example, there are two ways we can proceed.
Method 1 uses a single command:
clang -o gcd gcd-func.c gcd-driver.c |
This will compile the two .c files and link them (meaning finding references in one file to definitions in another) to produce an executable file which will be called gcd.
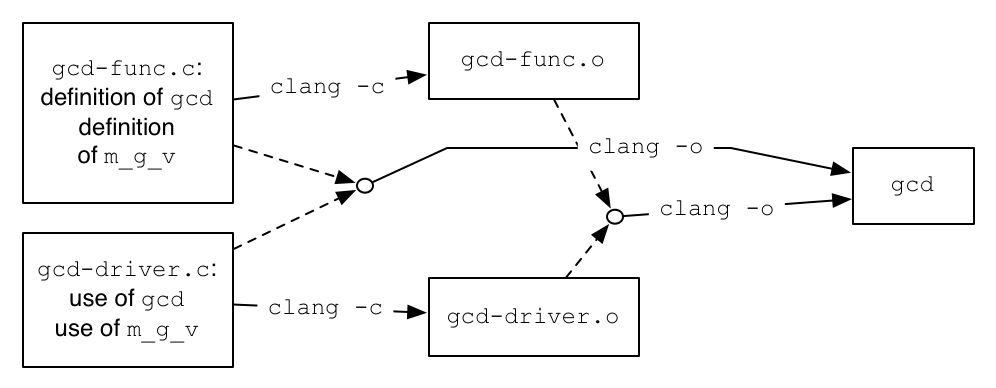
Method 2 uses three commands:
clang -c gcd-func.c |
clang -c gcd-driver.c |
clang -o gcd gcd-func.o gcd-driver.o |
The end result is the same as Method 1, though two extra files (gcd-func.o and gcd-driver.o) are created. These are "object files", containing executable code together with information about unsatisfied references. Here is a pictorial diagram of the effect of the commands.
To test your understanding of the process, consider the command from Method 1, and the following questions, which represent common errors:
clang -o gcd gcd-func.c gcd-driver.c |
What if we forget to include gcd-func.c in the command?
What if we forget to include gcd-func.c?
What if we forget to include gcd-driver.c?
What if we forget to say #include "gcd.h" in gcd-driver.c?
You should be able to reason out what might happen in each case (though maybe not the precise wording of any errors reported). Whether you can successfully reason about what might happen, or not, try these experiments to familiarize yourself with these common errors in advance.
Though Method 1 is simple enough that you can use it for all programming exercises here, Method 2 scales up to programs that involve many files. With Method 2, if you change one file, you can recompile just that file, and then relink to create a new version of the executable, which is less work than compiling all the unchanged files again.
2.4 Iteration
Here are two functions that sum up the numbers from 0 to n, one using structural recursion on natural numbers, the other using accumulative recursion.
| (define (sum1 n) |
| (cond |
| [(zero? n) 0] |
| [else (+ n (sum1 (sub1 n)))])) |
| (define (sum2 n) |
| (define (sum-helper n s) |
| (cond |
| [(zero? n) s] |
| [else (sum-helper (sub1 n) |
| (+ n s))])) |
| (sum-helper n 0)) |
In a typical Racket course of study, there is no reason to prefer one over the other. Each one takes time linear in the value of the parameter n. If you know order notation, they take \(O(n)\) time. We can easily translate these into recursive C programs.
int sum1(int n) { |
if (n == 0) { |
return 0; |
} else { |
return n + sum1(n - 1); |
} |
} |
|
int sum_helper(int n, int s) { |
if (n == 0) { |
return s; |
} else { |
return sum_helper(n-1,n+s); |
} |
} |
|
int sum2(int n) { |
return sum_helper(n,0); |
} |
These are legal and correct C functions, but neither one represents the way this task is commonly (or idiomatically) performed in C.
C provides special language constructs for iteration or repetition. (I’ll discuss the reasons for this preference below.) The three loop constructs in C are while, for, and do. As with if, these constructs do not produce values, but get work done through side effects.
Here is an example of how the sum function might be implemented in C, using a while loop.
int sum(int n) { |
int s = 0; |
while (n != 0) { |
s = s + n; |
n = n - 1; |
} |
return s; |
} |
The general form of a while loop is while (<cond>) <body>, where <cond> is a Boolean expression, and <body> is a single statement or a block.
The semantics of a while loop are as follows. The condition is evaluated. If it is not false (0), the body is evaluated. This is repeated until the condition is false. As with other C statements we have seen, neither the body nor the whole loop produces a value; work gets done entirely through side effects.
Here is an implementation using a different but related construct, a for loop. Note that C99 permits a loop variable to be declared inside the for header. In earlier C standards, the variable i would have to be declared along with s, outside the loop. This is still sometimes desirable, in case the final value of i is needed afterwards (it would be out of scope in the program below).
int sum(int n) { |
int s = 0; // C99 declaration below |
for (int i = 1; i <= n; i = i+1) |
s = s + i; |
return s; |
} |
The general form of a for loop is for (<initialize>; <condition>; <update>) <body>.
The initialization is done once. The condition is checked before every execution of the body (which could be a single statement or a block). The update is done after each execution of the body.
Here is an example of using two nested for loops to compute all perfect numbers less than or equal to 10000. A perfect number is one which is equal to the sum of its divisors (including 1 but excluding itself). This is not the best way to compute perfect numbers, since they are rare and, at least for the range given, must be of a specific form. But it does illustrate nested loops.
int main(void) { |
int i = 0; |
int j = 0; |
for (i=1; i <= 10000; i++) { |
int acc = 0; |
for (j=1; j < i; j++) { |
if (i % j == 0) { |
acc = acc + j; |
} |
} |
if (acc == i) { |
printf("%d is perfect\n", i); |
} |
} |
} |
In my CS 146 course, I discussed this program and how this computation might be carried out in several languages (including Racket, Haskell, and Python), and compared the actual running times. It may surprise you to learn that Racket was faster than Python, and that Haskell was the same speed as C with a far shorter and more declarative program. But here I merely note that it is a good example of the use of nested loops.
2.5 The computational model
The C computational model is similar to the one I develop for the languages used in FICS or to any von Neumann machine: it maintains a notion of the current location in the program and the current contents of memory. The current location in the program may be a statement or it may be within a statement, as described below (for example, in the execution of an assignment statement with a function call on the right-hand side). The metaphor of keeping a finger on the program and moving it as statements are executed comes in handy.
We need to refine our view of memory slightly.
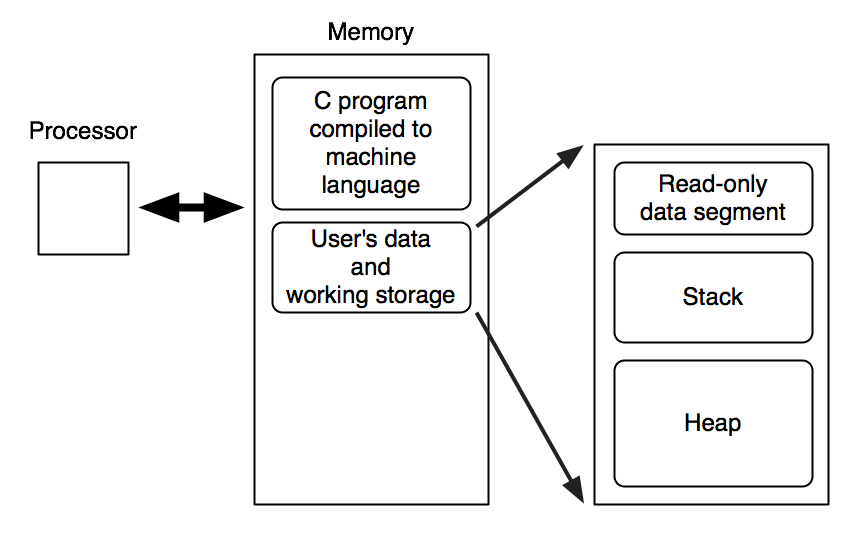
The new regions of memory listed in this diagram (stack, heap, and read-only data segment) will be discussed in what follows.
Let’s return to our simple program.
#include <stdio.h> |
int main(void) { |
int i = 5; |
int j; |
j = i + 1; |
printf("%d\n", j); |
return 0; |
} |
We’ll do an informal trace of this program, visualizing memory. We have to keep in mind that the C code is not being directly executed. Rather, it is compiled to machine code which is then executed. The value of the variable i is stored in memory, but of course the machine code has no notion of "i". It only deals with memory locations. However, there is some correspondence between some memory location and i, and we can think of this correspondence as being stored in a symbol table mapping names to locations. The table does not really exist at run time. It is a conceptual aid to understanding the effect of the program. Something like it may exist in the compiler while the C code is being compiled.
With those caveats, let us proceed to the trace.
After int i = 5; int j has been executed:
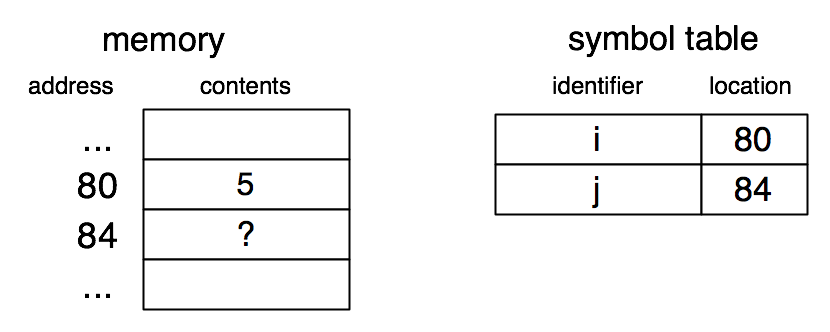
We use a question mark to indicate that the value of j is unknown, though in practice there will be some value in that memory cell.
After j = i + 1; has been executed:
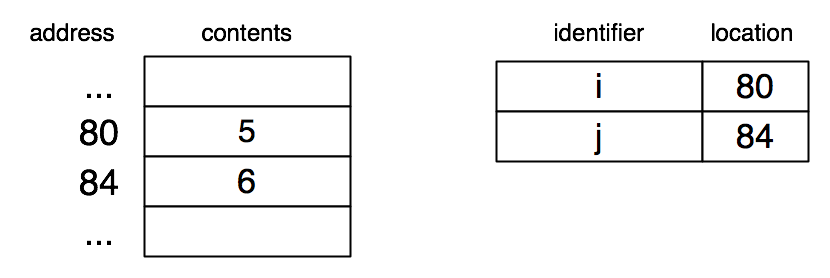
It is useful (not so much right now, but definitely later) to think of the left-hand side of an assignment as specifying an lvalue (a memory address) in which the rvalue (a C value) is stored.

Global variables (declared outside any function) can be assigned to a fixed location in memory for the duration of the program. But this is not the case for local variables in functions, especially recursive functions.
In FICS, I discuss the implementation technique typically used to handle function application in an imperative language in some detail. Here, I’ll simply describe and illustrate the technique.
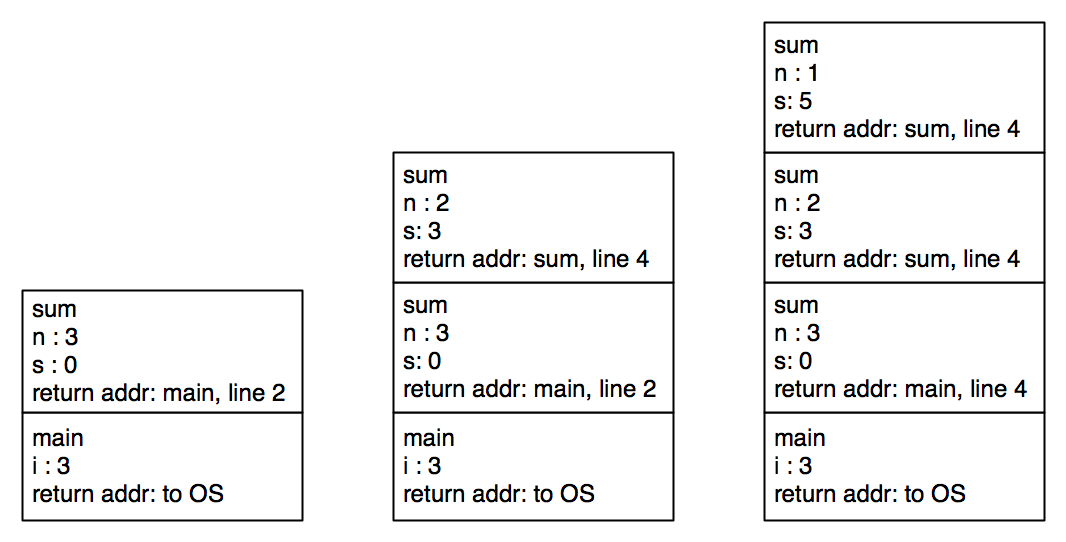
When a function is called, a stack frame is pushed (allocated at the "top" of the stack). The stack frame contains the argument values, space for the local variables used in that function, and the return address (location in the code where execution resumes once the function returns a value).
We will think of the stack as growing towards lower-numbered memory locations. We could just as well have a stack growing towards higher-numbered memory locations. There really is no conceptual difference, except that putting the new stack frame "on top" of the old one in the diagram fits the metaphor of a stack (of books or dishes) better.
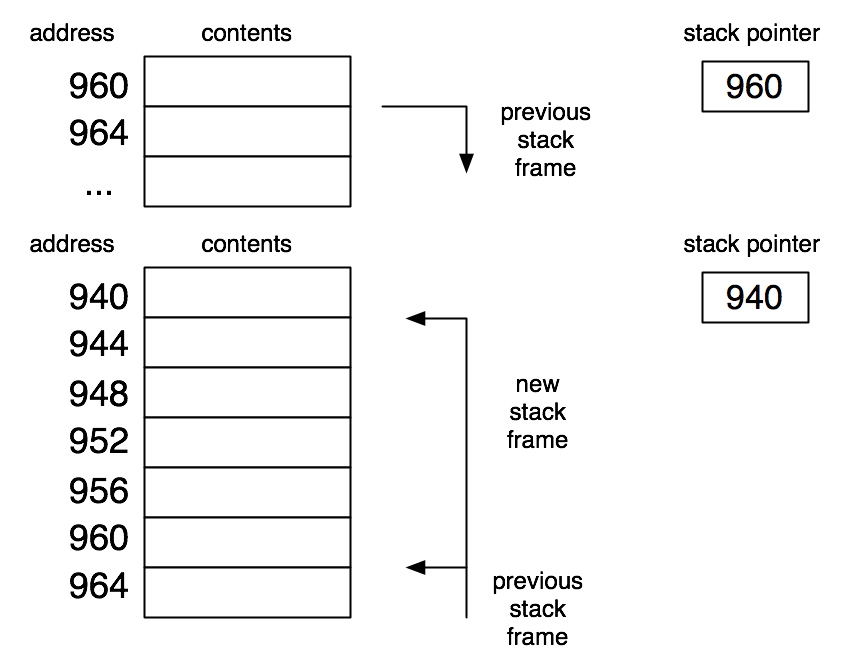
The "return address" of a function may not be a statement in the program. It may be within a statement or expression, as will be demonstrated by the following program.
int main() { |
int i = 3; |
printf("The sum from 1 to %d is %d\n", i, sum(i)); |
return 0; |
When this program starts executing, a stack frame is set up for main.

Here is the code for sum.
int sum(int n) { |
int r = 0; |
if (n != 0) { |
r = n + sum(n - 1); |
} |
return r; |
As execution proceeds, each call to sum sets up a new stack frame.
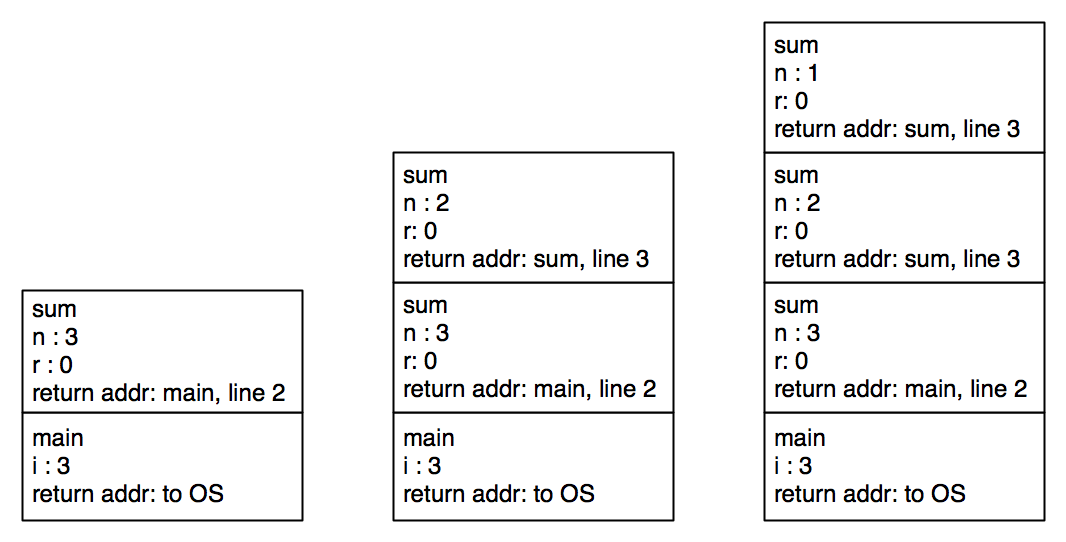
The stack reaches its maximum height when the base case is reached.

After that, values start being returned to earlier computations.

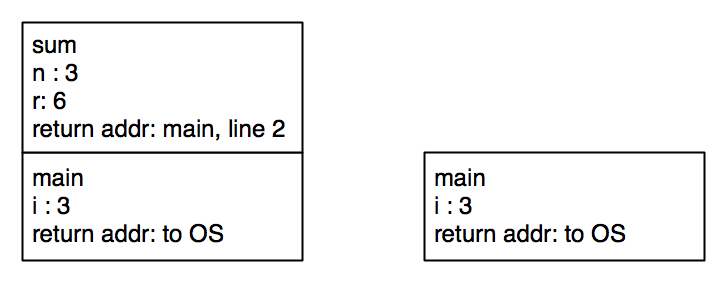
The memory model is required in order to understand recursion in C. There are a number of consequences of this. The main ones are that recursion is harder to understand, and recursion is more expensive, because it is not as optimized as it is in Racket. Racket’s optimizations are discussed in FICS.
Consider the following alternate method of computing the sum of the numbers from n down to zero, which is tail-recursive.
int sum(int n, int s) { |
if (n == 0) { |
return s; |
} else { |
return sum(n-1,n+s); |
} |
} |
|
int main() { |
int i = 3; |
printf("Summing 1 to %d gives %d\n", i, sum(i,0)); |
return 0; |
} |
By the interpretation above, this still uses \(n\) stack frames. But there is an obvious optimization. When sum recursively calls itself, there is no computation after the return. The return value is the value of the recursive call. So the stack frame can be reused. Instead of the stack growing:
We simply rewrite the values of n and s in the same stack frame:
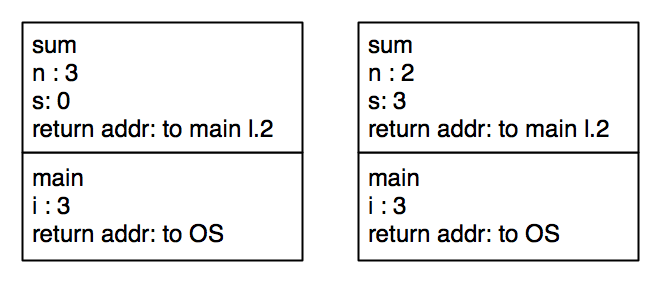
In this fashion, the computation can use only \(O(1)\) stack frames.
Racket, and in fact all Scheme implementations, optimize tail recursion in a similar fashion. C compilers may optimize tail recursion. clang and gcc often do; they will handle this program. But there are conditions under which they will not fully optimize tail recursion. And historically, C compilers did not do this. So, mostly, iterative constructs such as for and while are used instead. Recursion is not entirely avoided in C. It sometimes must be used for lists, and is often used for trees. But it is used much less often than in Racket.
2.6 Idiomatic use of loops
Here is a program that computes the same sum as above, but more idiomatically.
int sum(int n) { |
int s = 0; |
while (n != 0) { |
s += n; |
n--; |
} |
return s; |
} |
Here we see two new constructs. s += n is shorthand for s = s + n. There are a few other assignment operators of this sort. n-- is an expression that produces the value of n and has the side effect of subtracting one from n (though the old value is produced). In the code above we just throw the value away. --n does the subtraction first and then produces the new value. These constructs save a few characters, at the cost of making programs harder to read. They were originally designed to give hints to the compiler as to how to improve the translation into machine code. Compiler technology has improved considerably since C was first defined, so such hints are no longer necessary. I mention them here mainly to enable you to read C code written by others.
We can use loops to convert the tail-recursive gcd computation below:
int gcd(int n, int m) { |
if (m == 0) { |
return n; |
} else { |
return gcd(m, n % m); |
} |
} |
into an iterative computation:
int gcd(int n, int m) { |
while (m > 0) { |
n = m; |
m = n % m; |
} |
return n; |
} |
Actually, this code is wrong. It is a good exercise to figure out what it actually does. The problem is that the first statement in the body of the while changes the value of n, but the second statement requires the old value. Our first instinct is to change the two statements around:
int gcd(int n, int m) { |
while (m > 0) { |
m = n % m; |
n = m; |
} |
return n; |
} |
But this does not work either. (What does it do?) The correct solution is to preserve the old value of either m or n in a temporary variable. Here we choose n:
int gcd(int n, int m) { |
while (m > 0) { |
int temp = n; |
n = m; |
m = temp % m; |
} |
return n; |
} |
This example highlights the difficulty in reasoning about loops. The recursive code had the effect of changing n and m simultaneously. More generally, a loop body gets things done by incremental changes, and one must argue that all of those changes add up to the larger change one wants from each iteration. Even in a loop with only three lines, as above, this gets complicated, and it is easy to get it wrong.
We can use while in a driver program to read test cases from an input file. The problem is that we need something like read. There is a function called scanf provided, and it is powerful, but too easy to use incorrectly. (For those who are interested, the textbooks give details.)
We can avoid using scanf if we write our own input functions using getchar. As a warmup, let us write a program that counts the number of characters input.
#include <stdio.h> // standard I/O |
#include <ctype.h> // char predicates |
|
int main(void) { |
int ch; |
int count = 0; |
ch = getchar(); |
while (ch != EOF) { |
count++; |
ch = getchar(); |
} |
printf("Number of chars is %d\n", count); |
} |
To extend this basic idea, we will write functions to read natural numbers. It’s convenient to have something like peek-char from Racket, which provides the value of the character but does not remove it from the input stream. Unfortunately, the only way to do this in C is to read the character, and then "unget" the character – in effect, stuffing it back into the input sequence. This is a rather painful hack, and illustrates how C is often inelegant.
int peekchar() { |
return ungetc(getchar(), stdin); |
} |
We can then write helper functions to skip over whitespace and check for the existence of another non-whitespace character, and then use them to read a natural number.
void skip_whitespace() { |
while (isspace(peekchar())) |
getchar(); |
} |
|
bool has_next() { |
skip_whitespace(); |
return (peekchar() != EOF); |
} |
|
int read_nat() { |
int nc, ans = 0; |
skip_whitespace(); |
while (isdigit(peekchar())) { |
nc = getchar(); |
ans = ans * 10 + nc - '0'; |
} |
return ans; |
} |
Here is a driver program (minus the #include lines, which I will often omit for clarity).
int main(void) { |
int i = 0, j = 0; |
while (true) { |
printf("First number? "); |
if (has_next()) { |
i = read_nat(); |
} else break; |
printf("Second number? "); |
if (has_next()) { |
j = read_nat(); |
} else break; |
printf("GCD of %d and %d is %d\n", |
i, j, gcd(i,j)); |
} |
return 0; |
} |
2.7 Running time analysis of C programs
You can skip this section if you don’t know order notation, though you don’t have to know much about it. I discuss it at length in section 2.1 of my flânerie Functional Data Structures (FDS).
Informally, here is how we might analyze the running time of a loop: \begin{align*} & \mbox{time for initialization}\\ + ~ ~ ~ & \mbox{time for first loop termination test}\\ + ~ (~ &\mbox{number of times the loop is executed} \\ & ~~\times (\mbox {time to execute the loop body}\\ & ~~~~~~~~~ + \mbox {time for the loop termination test}\\ & ~~~~~~~~~ + \mbox {time for the loop update}))\\\end{align*}
The time taken by a sequence of statements (such as the body of a loop) is the sum of the times taken by each statement.
As an example, consider a generalization of the perfect number program which finds all perfect numbers up to and including a supplied value of \(n\) (instead of 10000).
int main() { |
int n = read_nat(); |
for (int i=1; i <= n; i++) { |
int sum_divs = 0; |
for (int j=1; j < i; j++) { |
if (i % j == 0) { |
sum_divs = sum_divs + j; |
} |
} |
if (sum_divs == i) { |
printf("%d is perfect\n", i); |
} |
} |
return 0; |
} |
This program takes \(O(n^2)\) time. Here is the informal reasoning. The body of the innermost loop (with loop variable j) takes \(O(1)\) time. It is repeated \(O(i)\) times, but i is bounded above by n, so this is \(O(n)\) time. The other statement in the outer loop takes \(O(1)\) time, so the total time for one iteration of the outer loop is \(O(n)\) time. Finally, the outer loop is repeated \(O(n)\) times, so the total running time is \(O(n^2)\).
Or is it?
The maximum size of an integer is \(O(1)\). So consider the following loop:
for (int i=1; i <= n; i++) { ...} |
Since n is an integer and thus \(O(1)\), we can claim that the loop body is executed \(O(1)\) times!
By this logic, arguably, the whole perfect number program takes \(O(1)\) time.
This may be technically true, but this is not useful. We usually pretend numbers are unbounded for the purposes of analysis, even though they are not. That preserves the analysis of the perfect number program above, as taking \(O(n^2)\) time. Our pretending only goes so far; we still assume that arithmetic operations take \(O(1)\) time, and this is not true for unbounded numbers, though it is true for bounded 32-bit integers.
2.8 Testing C programs
The absence of mutation made testing in the Racket teaching languages fairly straightforward. Things get more complicated, even in Racket, when mutation is involved. The general remarks about testing in the presence of mutation that I make in FICS (about Racket) also apply here. However, the situation is even worse for C, because mutation is so pervasive, and because the printf function in C only knows how to print simple types. It cannot print the C equivalent of structures, lists, or trees.
The ability to use interaction and to work on the command line offers one way to automate visual tests. We can use printf to format the output as we wish and capture it in a file using file redirection. As a simple example, consider myprog.c:
int main(void) { |
int x = 3; |
printf("Test 1: x is %d\n", x); |
x = 4; |
printf("Test 1: x is %d\n", x); |
} |
We can then prepare a text file (say expected.txt) that contains the output we expect.
Test 1: x is 3 |
Test 2: x is 4 |
Be careful: when preparing such a file on a Windows system, you need to be aware that the default Windows convention for ending lines is with two characters ("carriage return" and "line feed"), while the default for Unix is one character (just "line feed"). You should always prepare such files with an editor run through Cygwin, and look at them either by using a command such as cat or by reading them into an editor run through Cygwin.
The final task is to run our program (here we assume it is compiled to myprog), redirecting the output to another text file (say output.txt), and then compare the two text files (actual output and expected output) using the Unix utility diff.
./myprog > output.txt |
diff output.txt expected.txt |
If the two files are identical, diff will not print anything. If the two files are different, diff will produce instructions on how to convert one file into another, which in our context is unnecessary.
This is similar to the method we often use at my university to autotest large numbers of student programs.
When we test a Racket function, we typically design many small directed tests. For example, we may test a function that consumes lists on the empty list, a list with one element, and so on. When one of these tests fails, it is usually easy to identify the incorrect part of the program, as opposed to having a test fail on a large list that exercises every line of code.
The same considerations apply to designing tests for a program that processes input and/or produces output. We may wish to test it on an empty file, a file containing one character, a file containing just a newline character, and so on. But typing all those commands in the shell each time we want to test is a nuisance.
Shell commands can be collected in programs, commonly called scripts, and run with a single command. The example below, testing a C program that uses both input and output and is compiled to myprog, uses the scripting language sh (others can be used):
#!/bin/sh |
./myprog2 < test1-in.txt > test1-out.txt |
diff test1-out.txt test1-expected.txt |
./myprog2 < test2-in.txt > test2-out.txt |
diff test2-out.txt test2-expected.txt |
If this code is saved in the file tests.sh and run with the command ./tests.sh, it will find differences between expected and actual output.
We are not using any of the programming language features of sh in this example, just running a sequence of commands. You can learn about the programming capabilities of various shells in a good Unix reference book or Internet tutorial.
You can see that testing, when scaled up, raises many of the same issues that programming itself does. We need ways of organizing and maintaining test suites.
2.9 C compile errors
The C compiler will report syntax errors in your program, or semantic errors that can be caught at compile time (e.g. type mismatches), but often its messages are not immediately understandable. Sometimes this is because your error results in something which is legal or looks almost legal. For example, a common error is to forget to end a structure definition with a semi-colon. This "glues on" the next thing following the definition, and the compiler proceeds to try to interpret that. It may be legal, or it may result in any of several error messages.
Here are some other common errors.
implicit declaration
The compiler works on your code in a top-down fashion. If you use a function or variable before defining it, the compiler will assume everything has type int. This is typically wrong, and your correct definition later on will cause a type mismatch.
If the function being implicitly declared is one you expect to be available, like printf, then you have forgotten the #include <stdio.h> line. If it is one that you thought you wrote, you probably forgot to mention the file in which it is defined in the compile command.
type mismatch
This could happen in an assignment statement where the lvalue and rvalue have different types, or it could happen if you are writing a function for which there is also a prototype, and the return type or some parameter type doesn’t match.
undefined symbol
This is a linker error, seen in a multi-file situation where a symbol (name of a variable or function) is used but never defined. If the symbol is main, it means that you either forgot to write a main function, or you didn’t include the file with your main function in the compile command.
multiple definitions
This is the opposite of the previous error: too many definitions of a variable or function. An easy way to make this mistake is to #include, for example, blat.c file instead of blat.h Typically blat.h file contains function prototypes and extern variable declarations, and there can be many of these. But typically blat.c contains actual definitions, and there can be only one of these. Rather than #include-ing blat.c, it should be present in the compile command as one of possibly several files to be compiled and linked.
If your program compiles without errors and runs to completion, but does not produce the expected output, there is no REPL (read-evaluate-print loop) in which to write test expressions. A crude but usually effective method is to add additional printf statements showing the value of various variables or data structures. This does not scale up well to larger programs, but should work for programs of the size encountered here. A debugger such as GDB (briefly described later) typically permits one to stop execution of a program at certain points and inspect the value of variables or memory locations. Programmers who work with C should learn to use such tools eventually, but it is up to you as to whether you should learn about them now.
2.10 Introductory Exercises
The first four exercises are designed to be completed using only integer variables and arithmetic, and loops. Do not use library functions (apart from printf), structures, arrays, or any other advanced language features. The point of these introductory questions is to get you used to the logistics surrounding writing and testing C programs. For more benefit and challenge, try to improve the efficiency of your solutions while keeping your code readable.
I suggested to students that they should prepare two files for each question. For the first exercise (as an example), the file C0.c should contain the definition of the required function (called isqrt) as well as any helper functions and #include statements that are needed. The file C0-driver.c should contain your main function which tests your implementation of isqrt, and should contain the line:
#include "C0.h" |
It’s a good idea to include the above line in C0.c also, just to catch inconsistencies. You will compile your code by running clang, and then run the executable in the usual fashion.
clang -o C0 C0-driver.c C0.c |
./C0 |
This facilitated marking for my course, but it also introduces practices that facilitate testing for the programmer and scale up moderately, so it’s still a good idea here.
Exercise 0: Write a function isqrt that consumes a non-negative integer n and produces the largest integer less than or equal to the square root of n (that is, the integer square root of n).
Use only int variables. Your function should work for all legal non-negative integers. Note that these have a limited range, and any intermediate result computed by your program that involves integers that falls out of that range will be converted to an incorrect result that does fall in the range. You might wish to investigate this phenomenon. \(\blacksquare\)
5 5 |
7 1 |
Your program should be able to list all 18 ways to write 446265625 as the sum of two squares. \(\blacksquare\)
Exercise 2: A regular number is a positive integer all of whose prime factors are in the set \(\{2,3,5\}\). (1 is assumed to be regular.) Write a function regular that consumes a positive integer \(n\) and prints out all regular numbers up to (and possibly including) \(n\), one to a line, in increasing order.
It does not seem possible to give a solution to this question that requires only constant time per number printed under the restrictions suggested above. The classic C solution uses arrays and, of course, mutation. A purely-functional Racket version of that solution using lists is possible, though slightly more complicated. There are elegant functional solutions using lazy evaluation. \(\blacksquare\)
Exercise 3: Write a function prime_factors that consumes a integer n greater than or equal to 2 and prints the prime factors of n, one to a line, in increasing order. For example, the call prime_factors(60) would print:
2 |
2 |
3 |
5 |
\(\blacksquare\)