4 Intermediate C
In this chapter, we get further into aspects of C that are somewhat dubious, but are often used in idiomatic code. You don’t have to write code a particular way just because others do (unless the company you’re working for enforces a particular style) but you often have to read and modify code that others have written.
4.1 Pointer arithmetic
The following two function headers are equivalent.
int my_function(int A[], int n) { ... } |
int my_function(int *A, int n) { ... } |
In either case, in the code for my_function, A can be treated either as the name of an array or as a pointer to an integer. The header does not force one approach or the other.
The address of A[i] is computed by multiplying i by 4 (because A is an array of integers) and adding the address referenced by A. We can also perform this address computation explicitly in C code with the expression A + i. (The pointer arithmetic in this section can be used with pointers to any type, where 4 is replaced by the size of that type in bytes.)
The expressions *(A+i) and A[i] are identical as lvalues and as rvalues.
Here is a small example illustrating these ideas.
int *p, *q, A[3] = {9, 2, 5}; |
p = A; |
q = A; |
q++; |
Here is the situation illustrated in the memory model.

The expression q - p has value 1, because the difference between the two pointers is enough space to store one integer. The comparison q < p yields 0 (false).
It is easy to make a mistake when arithmetic operators are used on pointers in this fashion. It might help to remember the following.
adding an integer to a pointer, producing a pointer value;
subtracting an integer from a pointer, producing a pointer value;
subtracting a pointer from a pointer of the same type, producing an integer value.
We can use array notation with pointers and pointer notation with array names.
Since p points to the element of A of index 0:
A[0], *(A+0), *A, *p,
*(p+0), and p[0] all mean the same.
Since q points to the element of A of index 1:
A[1], *(A+1), *q,
*(q+0), and q[0] all mean the
same.
4.2 C strings
A string of length \(n\) in C is actually a character array of length at least \(n+1\), where the character at index \(n\) is the special null character represented by ’\0’. ’\0’ is actually the 8-bit pattern with all bits zero. It fails an if test. We can thus compute the length of a string (unlike a general array).
This is a simple idea, but leads to some complications, as well as being a significant source of security weaknesses. The first complication arises in the use of string constants.
The local declaration char title1[] = "CS 135"; results in space for seven characters being allocated on the stack. We can then assign to any element of this array. Here is the picture in the memory model.
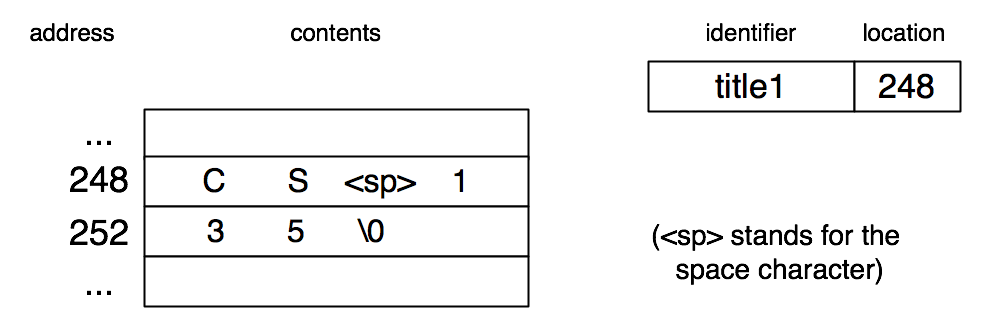
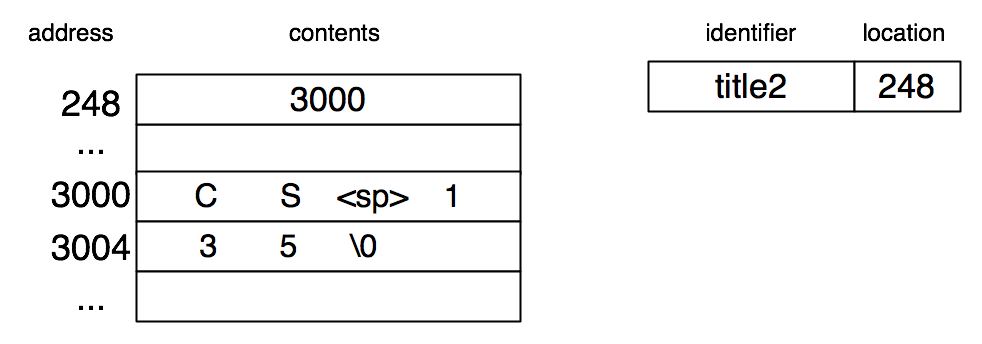
The local declaration char *title2 = "CS 135" results in space for one word (containing a pointer to a character) being allocated on the stack.
The seven characters are a string constant which might be shared if it occurs several times in a program. They may be allocated in read-only memory and should not be mutated (though the pointer can be).
As an example of how to manipulate strings with this convention, consider the example of copying a string.
The header file <string.h> provides prototypes a number of string utility functions, such as strcpy, which copies a null-terminated string from a source array to a destination array. We can write a version of this ourselves.
char *strcpy1(char dst[], char src[]) { |
int i = 0; |
while (src[i] != '\0') { |
dst[i] = src[i]; |
i++; |
} |
dst[i] = '\0'; |
return dst; |
} |
Idiomatic C code is briefer and more cryptic. Here is the same function rewritten.
char *strcpy2(char *dst, char *src) { |
char *p1 = src, *p2 = dst; |
while (*p1) *p2++ = *p1++; |
*p2 = *p1; |
return dst; |
} |
The key to understanding this code is the expression *p2++ = *p1++. This copies the byte pointed to by p1 into the byte pointed to by p2, moving both pointers to the next byte after using each one. This continues until p1 points to a zero byte, which is copied to terminate the destination string.
strcpy2 is probably not any faster than strcpy1, and it certainly is less readable. Neither version does any checking. The lack of checking can have serious consequences. Consider the following code.
char a[5]; |
char b[] = "This is way too long"; |
strcpy2(a,b); |
As with earlier examples of array indices out of bounds, the compiler will not complain, and there are no run-time checks. The compiled code, when run, will copy all of string b into the 21 bytes starting at what a points to. What damage is done depends on what is stored in memory after the 5 bytes of a. The program may fail later, inexplicably.
This method has been used to breach the security provided by poorly-written code, for example by entering a string that is too long into a Web form which processes its fields using C code.
Somewhat safer string routines include an integer bound. Here is a comparison routine that returns 0 if the two strings have up to the first \(n\) characters identical and 1 otherwise. (There is a prototype for a version of this in <string.h>, with a slightly different name and slightly different behaviour.)
int strcmpn(char *s1, char *s2, int n) { |
while (n > 0) { |
if (*s1 != *s2) return 1; |
if (*s1 == '\0') return 0; |
s1++; |
s2++; |
n--; |
} |
return 0; |
} |
We can use this function to search for the presence of a substring p in a string t. Note the use of pointers and pointer arithmetic to simplify the use of the helper function.
int search(char *t, char *p) { |
int i = 0; |
int plen = strlen(p); |
int tlen = strlen(t); |
while (1) { |
if (i+plen > tlen) return -1; |
if (strcmpn (t+i, p, plen) == 0) return i; |
i++; |
} |
} |
4.3 Reading S-expressions in C
Greenspun’s Tenth Rule of Programming (circa 1993) says:
Any sufficiently complicated C or Fortran program contains an ad hoc, informally-specified, bug-ridden, slow implementation of half of Common Lisp.
If this is the case, then we need translations into C of functions like read, which parses an input file in terms of S-expressions.
FICS includes a miniature version of read written in Racket. The difference here is that we need to manage memory explicitly in C. We also need to remove as much recursion as possible, without going too far. Finally, we will notice the need for some sort of type tag, and I will introduce the C feature called enumerations to assist with this.
Here is our definition of a node of the tree associated with a given S-expression.
struct node { |
enum {NAME, NUM, LST} tag; |
int num; |
char *str; |
struct node *sublst; |
struct node *rest; |
}; |
Note the use of an enumeration, which is an approximation of a restricted use of symbols in Racket. The symbolic names NAME, NUM, LST are actually translated to the constants 0, 1, 2 by the compiler, but we don’t have to worry about the exact translation (nor should we count on it in code we write).
The first line in the next code fragment is a directive to the C preprocessor to define a symbolic constant which will simplify our use of malloc. It is followed by the definition of a token for parsing purposes. A token is one of: left parenthesis, right parenthesis, string (name), integer (natural number, really), or end-of-file.
#define NSIZE sizeof(struct node) |
|
struct token { |
enum {LPAR, RPAR, STR, INT, TEOF} tag; |
int num; |
char *str; |
}; |
Here is the code for a function that reads a token from the input stream, followed by its helper functions. These are just elaborations on what we have seen before, and they’re not too hard to write using loops instead of tail recursion.
struct token read_token() { |
struct token t; |
skip_whitespace(); |
int c = getchar(); |
if (c == EOF) { |
t.tag = TEOF; |
} else if (c == '(') { |
t.tag = LPAR; |
} else if (c == ')') { |
t.tag = RPAR; |
} else if (isalpha(c)) { |
t.tag = STR; |
t.str = read_id(c); |
} else if (isdigit(c)) { |
t.tag = INT; |
t.num = read_nat(c); |
} else { |
printf("bad character: %c\n", c); |
abort(); |
} |
return t; } |
|
int read_nat(int c) { |
int ans = c - '0'; |
while (isdigit(peekchar())) { |
c = getchar(); |
ans = ans * 10 + c - '0'; |
} |
return ans; |
} |
|
char *read_id(int c) { |
char buf[100], *newstr; |
buf[0] = c; |
for (int i=1; i < 100; i++) { |
c = peekchar(); |
if (isalpha(c) || isdigit(c)) { |
buf[i] = getchar(); |
} else { |
buf[i] = '\0'; |
newstr = malloc(strlen(buf)+1); |
strcpy(newstr,buf); |
return(newstr); |
} |
} |
} |
Notice that we are limiting identifiers/names/strings to 99 characters, and using a single buffer as intermediate storage. We can remove this restriction by using the "doubling-up" technique described earlier.
Repeatedly calling read-token on input (a (1)) would result in this sequence of tokens:
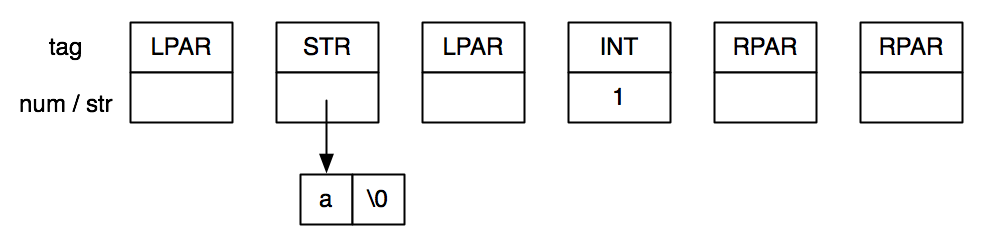
To simplify the previous diagram, I have combined the num and str fields, since only one is ever used. The C feature known as unions can actually accomplish this. If you’re interested in learning about this, consult a textbook or other reference.
With the tokenizing layer completed, we can now write the main read function. Note the use of recursion in the read_list helper function. This is acceptable, as the recursion depth is the depth of nesting of the expression being read, which is typically small. We’d have to do something else if this were not the case.
struct node *miread() { |
struct token t; |
struct node *newn; |
t = read_token(); |
if (t.tag == TEOF) { |
return NULL; |
} else if (t.tag == LPAR) { |
newn = malloc(NSIZE); // check! |
newn->tag = LST; |
newn->sublst = read_list(); |
return newn; |
} else if (t.tag == RPAR) { |
printf("unmatched right parenthesis\n"); |
abort(); |
} else { |
return token_to_node(t); |
} |
} |
|
struct node *token_to_node(struct token t) { |
struct node *newn; |
newn = malloc(NSIZE); // check! |
if (t.tag == INT){ |
newn->tag = NUM; |
newn->num = t.num; |
} else { // t.tag == STR |
newn->tag = NAME; |
newn->str = t.str; |
} |
return newn; |
} |
|
struct node *read_list() { |
struct token t; |
struct node *newn, *ans = NULL, **last = &ans; |
while (1) { |
t = read_token(); |
if (t.tag == RPAR) { |
*last = NULL; |
return ans; |
} else if (t.tag == LPAR) { |
newn = malloc(NSIZE); |
newn->tag = LST; |
newn->sublst = read_list(); |
} else if (t.tag == TEOF) { |
printf("unfinished list\n"); abort(); |
} else { |
newn = token_to_node(t); |
} |
*last = newn; |
last = &newn->rest; |
} |
} |
On input (a (1)), mi_read() returns a pointer to:
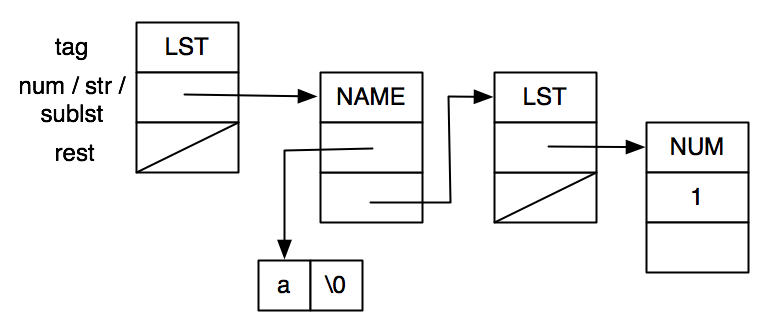
To verify that our code does what we expect, we need a routine that prints the contents of what mi_read produces. printnode consumes a pointer to an S-expression representation and prints out a suitable translation in Scheme syntax. Once again, we use recursion where appropriate and loops where it makes sense to do so.
void printnode(struct node *np) { |
if (np == NULL) { |
printf("()"); |
} else if (np->tag == NAME) { |
printf("%s", np->str); |
} else if (np->tag == NUM) { |
printf("%d", np->num); |
} else if (np->tag == LST) { |
printf("( "); |
printnodelist(np->sublst); |
printf(")"); |
} |
} |
|
void printnodelist(struct node *np) { |
while (np != NULL) { |
printnode(np); |
printf(" "); |
np = np->rest; |
} |
} |
Here is a small driver program.
int main() { |
struct node *np; |
while (1) { |
printf("Enter s-expression: "); |
np = miread(); |
if (np == NULL) break; |
printf("Representation: "); |
printnode(np); |
printf("\n"); |
freenode(np); |
} |
printf("\n"); |
return(0); |
} |
Just as printnode printed an entire S-expression representation, freenode will free the memory associated with one. Without this, the memory leak in the program would eventually result in malloc returning NULL (checks for which I have left out here).
void freenode(struct node *np) { |
if (np->tag == LST) { |
freenodelist(np->sublst); |
} else if (np->tag == NAME) { |
free(np->str); |
} |
free(np); |
} |
|
void freenodelist(struct node *np) { |
struct node *tmp; |
while (np != NULL) { |
tmp = np->rest; |
freenode(np); |
np = tmp; |
} |
} |
This example contains many of the elements that one needs to code in order to deal with data structures in C, namely ways to create, print, and free such structures. Debugging such code can be frustrating, because if the data structure is messed up, attempting to print it will probably result in an error.
4.4 Other representations of trees
The representation for a binary tree (below, a binary search tree) is very similar in Racket and C, though the code may be different.
(define-struct node (key value left right))
struct node { |
int key; |
char *value; |
struct node *left; |
struct node *right; |
}; |
We can write code that implements the mutable Table ADT.
struct node *add_bst1(struct node *t, int k, char *v){ |
if (t == NULL) { |
t = malloc(sizeof(struct node)); |
if (t == NULL) { |
printf("out of memory\n"); |
abort(); |
} |
t->key = k; |
t->value = v; |
t->left = NULL; |
t->right = NULL; |
} else if (k == t->key) { |
t->value = v; |
} else if (k < t->key) { |
t->left = add_bst1(t->left,k,v); |
} else { |
t->right = add_bst1(t->right,k,v); |
} |
return t; |
} |
|
int main(){ |
struct node *t = NULL; |
t = add_bst1(t,7,"test1"); |
t = add_bst1(t,4,"test2"); |
t = add_bst1(t,12,"test3"); |
print_bst(t); |
printf("\n"); |
} |
I have not included the code for print_bst.
As described earlier, an alternative to the awkwardness of producing a new pointer to the root of the tree is to pass in a pointer to where the root is located. We could then say add_bst2(&t, 5, "test") to do the same thing as t = add_bst1(t,7,"test1").
void *add_bst2(struct node **tloc, int k, char *v){ |
struct node *new, *t; |
if (*tloc == NULL) { |
new = malloc(sizeof(struct node)); /* check! */ |
new->key = k; |
new->value = v; |
new->left = NULL; |
new->right = NULL; |
*tloc = new; |
} |
t = *tloc; |
if (k == t->key) { |
t->value = v; |
} else if (k < t->key) { |
add_bst(&(t->left),k,v); |
} else { |
add_bst(&(t->right),k,v); |
} |
return t; |
} |
There are a number of possibilities for representing trees of arbitrary fanout (not just binary).
Idea 1: '(1 (2 5 6 7) 3 4) represents a node-labelled tree.
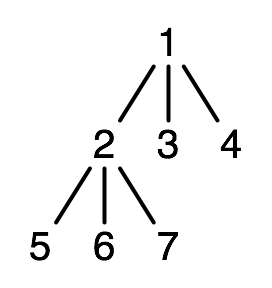
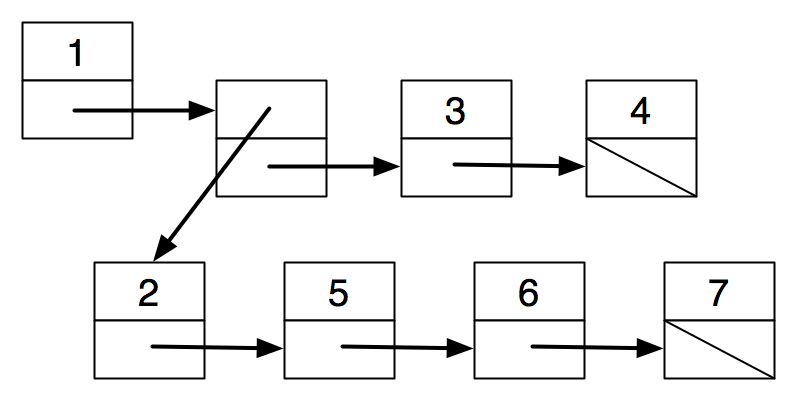
Idea 2: a list of children.
struct node { |
int value; |
struct node *next; |
struct node *children; |
} |
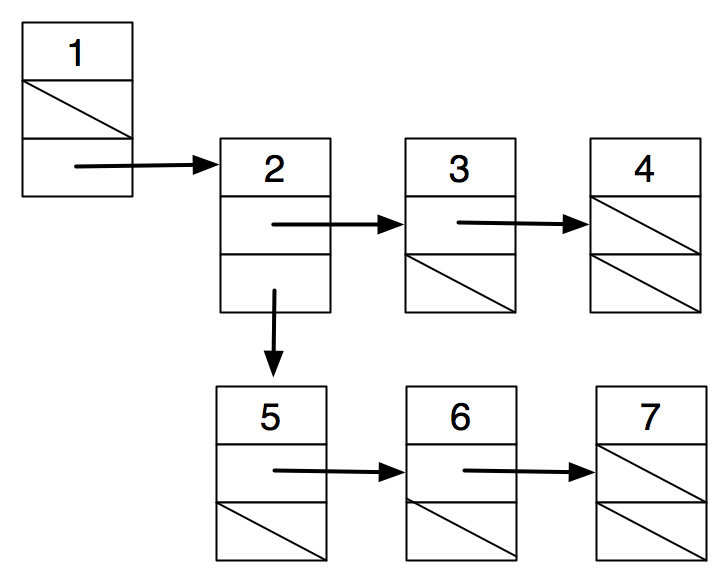
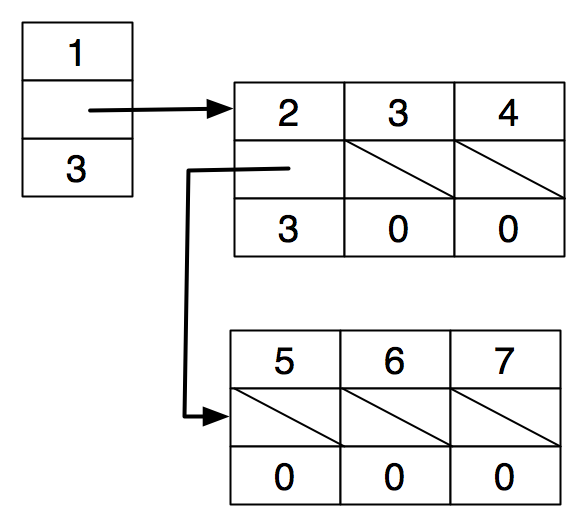
Idea 3: use an array of children.
struct node { |
int value; |
struct node *children; |
int nchildren; |
} |
4.5 Algorithms using arrays
4.5.1 Mergesort
FICS discusses bottom-up list-based mergesort in Racket (and FDS uses it as an early OCaml example). Here, we will implement bottom-up array-based mergesort in C. Instead of starting with lists of size 1 and merging in pairs, we will start with subarrays of size 1 and merge in pairs. As with the Racket code, we keep merging until we have one sorted array. Here is how the merging of two subarrays of size 4 into one sorted subarray of size 8 might look, before and after.
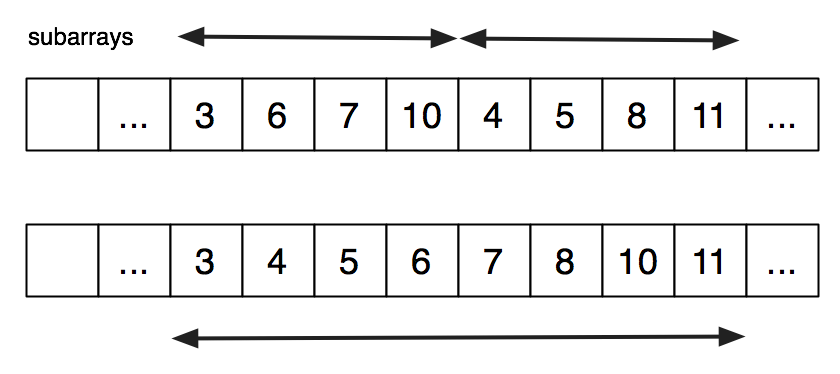
To do the merge, we merge into a segment of a work array and then copy back. The bound on the subarrays, the places from which information is being taken, and the place it is going are all described by integer indices. Here is a possible snapshot of the middle of a merge, using index variables declared in the following code.
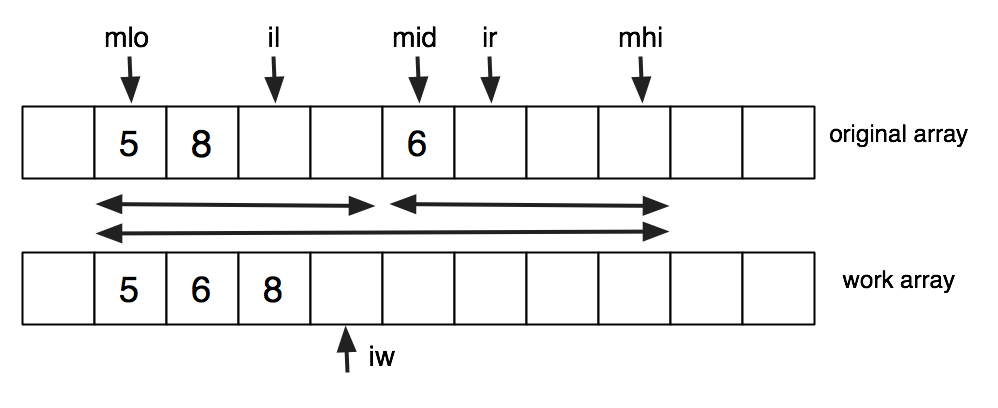
void merge(int a[], int work[], |
int mlo, int mid, int mhi) { |
int il, ir, iw; |
il = mlo; |
ir = mid; |
iw = mlo; |
while (il < mid && ir <= mhi) { |
if (a[il] < a[ir]) { |
work[iw++] = a[il++]; |
} else { |
work[iw++] = a[ir++]; |
} |
} |
while (il < mid) work[iw++] = a[il++]; |
while (ir <= mhi) work[iw++] = a[ir++]; |
for (iw = mlo; iw <= mhi; iw++) a[iw] = work[iw]; |
} |
Exercise: write this code using pointers and pointer arithmetic.
We now need a function which repeatedly merges pairs of subarrays until there is only one.
void msort(int a[], int work[], int n) { |
int i, msize, mlo, mhi, mid; |
for (msize = 1; msize < n; msize = msize * 2) { |
for (i = 0; i < n; i = i + (msize * 2)) { |
mlo = i; |
mid = i + msize; |
/* odd # of subarrays? */ |
if (mid >= n) break; |
mhi = i + (msize * 2) - 1; |
/* short last subarray? */ |
if (mhi >= n) mhi = n - 1; |
merge (a, work, mlo, mid, mhi); |
} |
} |
} |
One reason to keep an array sorted is that we can search more rapidly for a given value, using the fact that access to any element takes constant time.
4.5.2 Binary search
FICS covers binary search in Racket. Here is what it looks like in C. The array A has n elements sorted in non-decreasing order. The goal is to search for key, producing the array index if it is found, and -1 if it is not in the array. Intuitively, the algorithm probes the middle element, and then recursively searches the first or second half. Here a loop is used, maintaining the endpoints of the subarray under consideration.
int binsearch(int A[], int key, int n) { |
int low = 0; |
int high = n - 1; |
while (low <= high) { |
int mid = (low + high) / 2; |
if (key < A[mid]) { |
high = mid - 1; |
} else if (key > A[mid]) { |
low = mid + 1; |
} else { |
return mid; |
} |
} |
return -1; |
The code maintains the invariant that if key is in
A[i],
then low \(\le\) i \(\le\) high.
This is the key to proving correctness of the algorithm. We prove that it is true
when we enter the loop; we prove that the loop body preserves the invariant;
and we prove that when the loop terminates (perhaps by the return statement
within the loop), the answer produced is what we want.
We can also show that the running time of this algorithm is \(O(\log n)\). Intuitively, the quantity high - low is cut in half each time. The details are a little messy.
It is not easy to get this code right, especially for versions that try to optimize the number of comparisons done.
4.6 Enforcing abstraction
There are two desirable properties of built-in types that we would like to extend to user-defined types. Built-in types are immune to tampering: we cannot access or modify any information about instances beyond what the associated functions do. Built-in types are immune to forgery: we cannot create instances except via the associated functions.
Immunity to tampering and forgery makes code less brittle (less prone to breaking when modified or extended). We would like to achieve this for our abstract data types. Unfortunately, there is no fully safe mechanism to do this in C. We can only approximate safety.
One way of hiding implementation detail is to use the typedef keyword to create a synonym for a compound type.
typedef struct node { |
int first; |
struct node *rest; |
} *int_list; |
With this definition, int_list is now a synonym for node *. We can now write code such as:
int_list append(int_list lst1, int_list lst2); |
To implement the queue ADT in C, we can put the code and associated global variables into a file queue.c. This can be compiled and distributed in object file form, say as queue.o.
We can also prepare a header file queue.h, which contains only prototypes of the functions and references to any needed global variables with extern added.
To use the queue functions, the file app.c can #include "queue.h", followed by code which uses the functions. app.c can be separately compiled without error, and the resulting app.o linked with queue.o to create an executable.
Here is a possible queue.h.
struct node; |
|
typedef struct { |
struct node *head; |
struct node *tail; |
} queue; |
|
queue make_queue(); |
void enqueue(queue q, int i); |
int dequeue(queue q); |
int front(queue q); |
int queue_empty(queue q); |
The typedef in queue.h exposes some internal details, which the person writing app.c can see just by looking at it. Here, the definition of struct node is not provided, so nothing much can be done with that information. But in the int_list example, someone seeing that typedef in a header file could write code declaring a variable p of type int_list and then write p->first, which violates the abstraction.
There is a way to avoid this to some extent. The mechanism we use is the same one that lets us avoid exposing the definition of struct node. Because we are declaring a pointer, and all pointers have the same length, the compiler knows the size of queue and can generate code using it. So we’ll define a type aqueue which is a pointer to queue, and only put that in queue.h.
struct queue; |
typedef aqueue *queue; |
aqueue make_queue(); |
void enqueue(aqueue q, int i); |
int dequeue(aqueue q); |
int front(aqueue q); |
int queue_empty(aqueue q); |
It is more awkward to write code for these functions in queue.c. We have to keep using indirection on the pointer to the queue header. But the writer of app.c sees no information on which they can act, except what we want them to see.
However, another security hole remains. The writer of app.c could provide their own definition of queue along with the function prototypes from queue.h and then link their code with queue.o. This is foolish, but not forbidden.
Data abstraction in C is a matter of convention, rather than it being enforceable by the language. C++ does a better job in this respect.
4.7 Intermediate Exercises
Exercise 7: At one point, when one searched in the online catalogue of the University of Waterloo library for an author’s last name, and there were several authors with that name, it responded with the first one (that is, with the lexicographically-first first name). If there was no author with that name, it showed one the place where that name would have been (just in case something nearby was what one wanted).
The binary search code presented above doesn’t work like that. It works if there are several numbers matching the search key, but it doesn’t give you the first one, and it doesn’t give you any useful position information if the search key is not in the array.
Your task in this exercise is to write an improved version of binary search. The function
int lowsearch(int A[], int key, int n);
returns the minimum index \(i\) such that \(A[i] \ge \mathit{key}\), or \(n\) if no such index exists (that is, \(A[i] < key\) for all \(0 \le i < n)\).
You will use the basic idea of binary search, aiming at an \(O(\log n)\) algorithm, but you may have to make many small changes – to the initialization, to the loop condition, to the body of the loop, and to what is returned. You can do it with only one comparison in the body of the loop. Getting the details right may be easier if you can write down an invariant, as discussed above, that is always true at the top of the loop. \(\blacksquare\)
Exercise 8: In this question, you will implement simple hash tables in C. Here are some suggested definitions.
struct anode { |
int key; |
char *value; |
struct anode *next; |
}; |
|
struct hash { |
int size; |
struct anode **table; |
}; |
The table field in the hash structure will be a pointer to an array of pointers, each one pointing to an association list for keys that hash to that index value. The size of the array will be stored in the size field. For the hash function mapping a key to an index, you can use key % size, or you can read the chapter on Hashing in FDS for more realistic suggestions.
Write and test the following functions.
struct hash make_table(int s); |
char *search(struct hash T, int k); |
void add(struct hash T, int k, char *v); |
void free_table(struct hash T); |
make_table initializes an empty hash table where the array has size s. search searches for the string associated with key k in table T (producing a pointer to it, or NULL if it is not there). add stores in T the key k with associated string value v. Note that a copy of the string must be made, because the driver program may mutate the string. free_table frees all heap-allocated memory used by T.
Do not use recursion, and ensure that your code has no memory leaks.
Implement a delete function that removes a key and its associated value from a hash table:
void delete(struct hash T, int k); |
\(\blacksquare\)
Exercise 9:
This is a C version of a Racket question in FICS.
This question involves a simple simulation of memory allocation and deallocation. The "memory" used will be a globally-declared integer array memory of size MSIZE (where MSIZE is a defined constant). A "cons cell" will be two consecutive words of this array (the words at index 0 and 1 are not used). A "pointer", then, is just a nonzero even index less than MSIZE. Index 0 will be our version of NULL, which we’ll call EMPTY.
You will write the C function int cons(int fst, int rst) which produces a "pointer" to a "cons cell", and the function void give_back(int ptr), which gives back a "cons cell" previously obtained using cons. These simulate malloc and free, respectively. Your code should not use malloc and free at all. cons can be used by the driver program to build "lists".
To aid in allocation, the global variable int next_mem will be a "pointer" to the next word of "memory" available. It starts at 2 and increases as necessary. We need to reuse "cons cells" that have been given back, so the global variable int free_list will be a "pointer" to a "list" of freed "cons cells". cons should take a cell from the free list if possible, and give-back should add to the free list. The diagram below illustrates a possible snapshot of the situation.
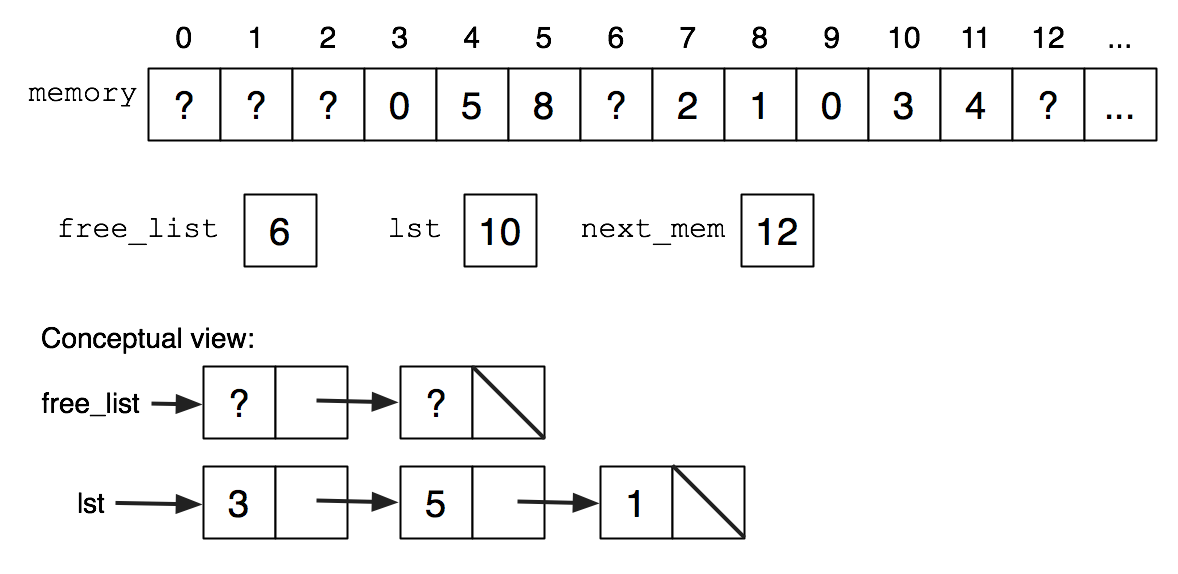
Your code should satisfy the following invariants: if at some point, the driver program has made \(c\) calls to cons, \(g\) calls to give_back, and the length of the free list is \(f\), then next_mem is \(2(c-g+f+1)\). Also, if \(f>0\) or if \(2(c-g+1)<\mathtt{MSIZE}-1\), then cons will be able to allocate a cell, otherwise it will fail. In this case, cons should print an error message.
Divide up your code in the following way. C9.c will contain code for the prototypes in C9.h, which in addition to cons and give_back, also include first and rest for the driver program to use. The global variables used for the memory simulation are declared in C9-mem.c, and the header file C9-mem.h declares those for use elsewhere (such as in C9.c). The driver program would normally just include C9.h, but you can include C9-mem.h if you want to look at the global variables in your tests. If the declaration of MSIZE is set small, you can more easily test out-of-memory situations, but make sure you have not assumed anything about its value. \(\blacksquare\)
Exercise 10: This exercise is also a C version of a Racket programming question in FICS.
To be or not to be |
Or not to be or to be |
To be or not to 1 |
Or 3 4 1 2 4 1 |
Write a C program that reads from standard input and writes the compressed version to standard output. You may choose your data structures. Try to make your program as efficient as possible. You may assume that there are at most 80 characters in any line. (For extra challenge, write a program that does not make this assumption.)
Then write a second C program that reads text from standard input, assumes that the text has been compressed in the manner described above, and writes the uncompressed text to standard output. The same comments about efficiency apply, and you may assume that there are at most 80 characters in any line. (Again, for extra practice, write a program that does not rely on this assumption.) \(\blacksquare\)
4.8 Acknowledgements
This work benefitted from the attention of Marc Burns, Thomas Baxter, and Kevin Matthews while it was being presented to students.
(Brooklyn, July 2020.)