3 Pointers
In Racket, the equal? predicate will compute whether two objects have the same value. But, under the hood, objects can share part of all of their structure, and there is typically no need to check whether two different variables or expressions in fact represent the same object (though this check is possible in Racket). Even in most other mainstream programming languages, which allow one object to explicitly reference another in order to build structures like lists and trees, one can only copy such references and compare them for equality.
In machine language or assembly language, everything is a 32-bit or 64-bit quantity. The same quantity can be interpreted as a signed integer by one instruction and as a memory address by the next instruction. C is in between these two extremes, but closer to assembly language. Memory addresses (or pointers) can be manipulated by arithmetic operations. This takes some getting used to.
3.1 Structures in C
Here is a simple declaration of a structure of type posn, with two fields x and y.
struct posn { |
int x; |
int y; |
}; |
Note the semicolon after the definition. This is important, and a frequent source of frustrating error when it is left out, since the resulting error message is not always very decipherable.
Here is an example of the use of structs. Note that the keyword struct must be used as part of the type. This is not the case in C++. If a variable is of type struct, one of its fields can be accessed by appending a dot and the field name to the variable name.
struct posn normalize(struct posn p1, struct posn p2) { |
struct posn ans; |
ans.x = p1.x - p2.x; |
ans.y = p1.y - p2.y; |
return ans; |
} |
|
float dist(struct posn p1, struct posn p2) { |
struct posn d; |
d = normalize(p1, p2); |
return sqrt(d.x*d.x + d.y*d.y); |
} |
|
int main() { |
struct posn p1 = {0,0}; |
struct posn p2 = {3,4}; |
float ans; |
ans = dist(p1, p2); |
printf("%f\n", ans); |
return 0; |
Each declared variable of type struct posn consists of two consecutive words of memory. For global variables, these two words are in some fixed location. For arguments and local variables, these two words will be in the stack frame associated with a call to the function in which they are used.
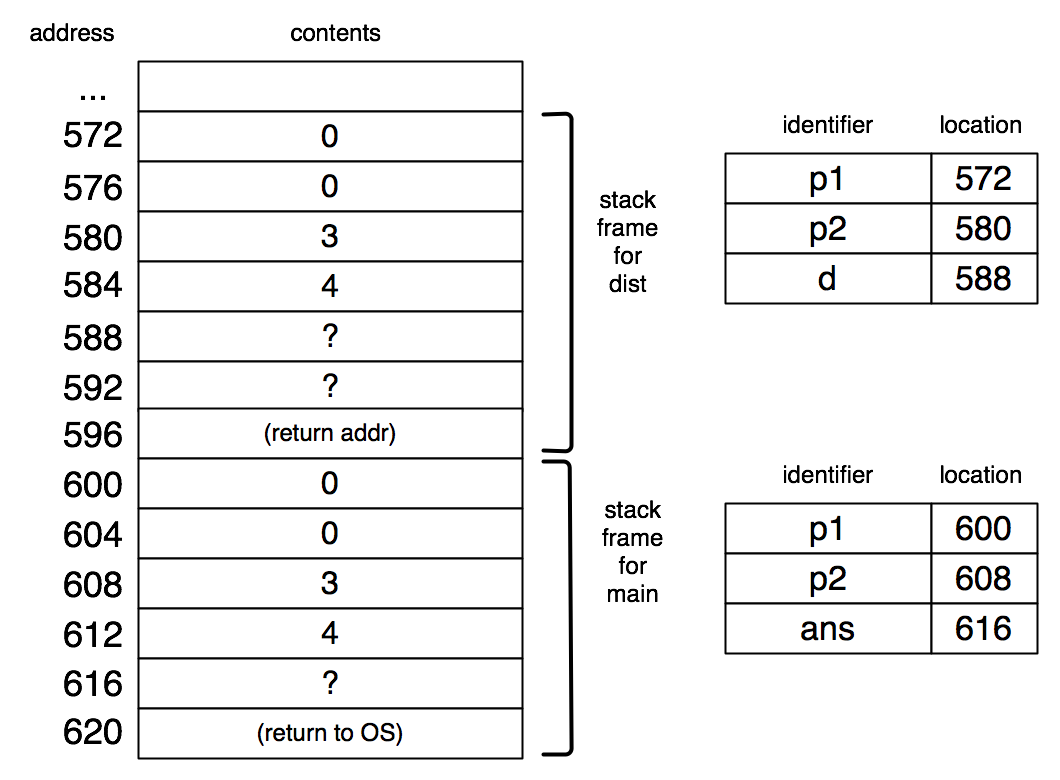
3.2 Pointers in C
A pointer, as described above, is a memory address. We can declare a variable of type "pointer to an int" as follows:
int *p;
Note that the * is attached to the name of the variable (p in this case), even though it is really part of the type. p is of type int *. This is unfortunate syntax, but we are stuck with it now.
One word is allocated to hold the value of the pointer p. That value will be interpreted as a memory address whose contents are an integer. p "points to" that integer.
The address-of operator & produces a useful pointer value when applied correctly.
int i = 1, j = 2, *p; |
p = &i; |
Below, the expression *p acts like the name of the integer to which p points. We can use *p as an lvalue or as an rvalue.
int i = 1, j = 2, *p; |
p = &i; |
*p = j + 1; |
j = *p + 2; |
When *p is an rvalue, its value is the value of the integer to which p points. But when *p is an lvalue in an assignment expression, the effect is to store the rvalue into the word of memory pointed to by p.
What follows is a rather artificial but nonetheless illustrative exercise in the semantics of pointers.
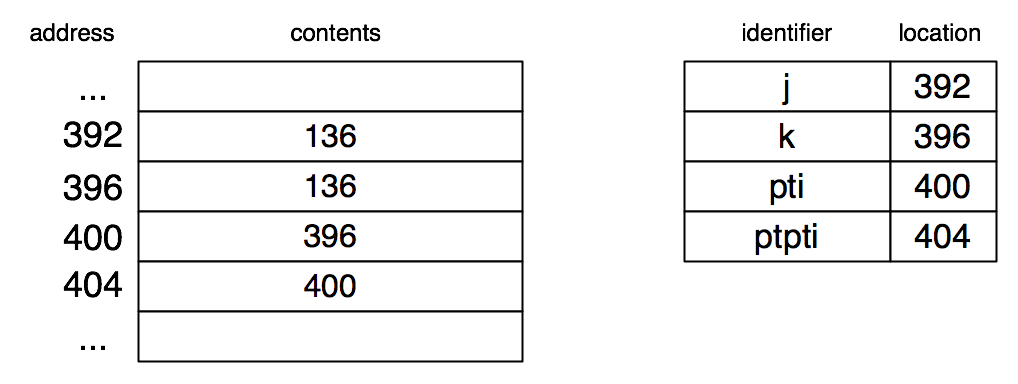
int main(void) { |
int j = 2666, k = 136; |
int *pti = &j; |
int **ptpti = &pti; |
*pti = 241; |
*ptpti = &k; |
j = **ptpti; |
**ptpti = 251; |
j = *pti; |
} |
After the initialization of j and k, we have the following situation:

Here is a table of the types of a number of expressions occurring in this program, as well as their interpretation as lvalues and rvalues.
Expression | Type | lvalue | rvalue |
j | int | 392 | 2666 |
k | int | 396 | 136 |
pti | int * | 400 | 392 |
*pti | int | 392 | 2666 |
ptpti | int ** | 404 | 400 |
*ptpti | int * | 400 | 392 |
**ptpti | int | 392 | 2666 |
We can now predict the effect of executing the next statement after the initialization, and continue with each subsequent statement.
*pti = 241;

*ptpti = &k;

j = **ptpti;
**ptpti = 251;

j = *pti;

If we want to call a function and mutate variables declared in the calling code, we can pass a pointer to such variables. This is known as passing variables by reference (as opposed to value, which is the method we saw earlier).
Example:
void swap(int *a, int *b), a function that swaps
the values of the two integers being pointed to.
swap(&i, &j) swaps the values in integer variables i and j.
void swap(int *a, int *b) { |
int temp; |
temp = *a; |
*a = *b; |
*b = temp; |
} |
We can illustrate the effect of this code using a small driver program.
int main() { |
int i = 2666; |
int j = 136; |
swap(&i, &j); |
printf("%d %d\n", i, j); |
return 0; |
} |
Before any assignment statements have been executed in swap:

temp = *a;

*a = *b;

*b = temp;

Don’t try this at home. The following program deliberately does something wrong to illustrate a common mistake.
#include <stdio.h> |
|
int *evil(void) { |
int j = 42; |
return &j; |
} |
|
int main(void) { |
int *pti = evil(); |
int k = *pti; |
printf("%d\n", k); |
return 0; |
} |
Here is a picture of what memory might look like just before evil returns:

After pti has been initialized in main:

At this point, *pti accesses memory location 592, whose contents are unpredictable. When last we looked, it held 42, but this is not guaranteed.
This is a potential source of error.
3.3 The NULL value
It is useful to have a pointer value that does not point to anything. Several header files (e.g. <stdio.h>) define the value NULL for this purpose. NULL is actually 0, and fails an if test. We will use it as we use empty in Scheme.
What happens if we try to apply the * operator to this value?
#include <stdio.h> |
|
int main(void) { |
int *p = NULL; |
printf("Disaster looms...\n"); |
printf("%d\n", *p); |
return 0; |
} |
When we save this program as starnull.c, compile it, and run the executable, it prints:
Disaster looms... |
Bus error |
A bus error occurs when the executable tries to access memory that does not exist. No indication is given of where the error occurred.
We can gain some information about the situation by using a tool known as GDB (GNU debugger).
If we add the -g flag to the compile command using clang, additional information is put into the executable. This information can be used by a debugger such as GDB.
We run GDB from the command line.
gdb starnull |
|
(gdb) |
The (gdb) is GDB’s prompt. There are many commands we can type, among them run. When we type run, we get:
Disaster looms... |
|
Program received signal EXC_BAD_ACCESS, Could not access memory. |
Reason: KERN_PROTECTION_FAILURE at address: 0x00000000 |
main () at starnull.c:6 |
6 printf("%d\n", *p); |
The meaning of this is that the program was halted when attempting to address memory location 0 while executing the translation of line 6 of the program. Information like this can point to where the error occurred in execution, but the real cause of it may be earlier in the program, when the pointer p was inadvertently set to NULL.
GDB has many more useful features which we will not discuss here. Type quit to leave GDB.
We said earlier that C is sometimes called "the portable assembler". But just how portable is C?
On some systems, starnull.c produces a segmentation fault, which is an attempt to access memory that exists but is not allocated to the program.
In general, erroneous programs may produce different errors on different machines, or may appear to work properly on some machines.
C programs can expose enough of the machine they are running on that even perfectly correct programs can exhibit different behaviour when compiled and run on different machines.
3.4 Heap allocation in C
Currently, we only have two ways to use memory. One is through global variables, which are visible everywhere and persist for the duration of the program, but the storage requirements must be known at compile time.
The other is through local variables, which can be brought into existence in the stack frame associated with a function call, but only persist for the duration of that call.
If we want memory for a data structure that is dynamic (created at run time) but lasts longer than a local variable, we need to use heap memory. The malloc function produces a pointer to a chunk of heap memory, given an argument which is the size of the memory chunk in bytes. Typically, however, we need space to store a fixed type (or later, several values of a fixed type). The size of a fixed type can vary depending on the machine, so instead, it is common to use sizeof, which looks like a function that consumes a type and produces the number of bytes it uses (it is actually an instruction to the compiler to substitute the actual size on the target machine, which means that you can use it to discover whether your programs are being compiled for 32-bit or 64-bit architectures).
Here is an example of the use of heap memory to store lists of integers.
#include <stdlib.h> |
|
struct node { |
int first; |
struct node *rest; |
}; |
|
struct node *cons(int fst, struct node *rst) { |
struct node *new = malloc(sizeof(struct node)); |
if (new == NULL) { |
printf("cons: out of memory\n"); |
abort(); |
} |
new->first = fst; /* same as (*new).first = fst */ |
new->rest = rst; |
return new; |
} |
Notice that malloc produces a NULL pointer if it runs out of memory. You should always do this check, though I will omit it in future examples to save space and improve readability.
Notice also the -> shorthand for extracting the field of a struct, given a pointer to it.
Here is a short program illustrating the use of our cons function. It prints 5.
int main() { |
struct node *lst1 = cons(5, NULL); |
struct node *lst2 = cons(3, lst1); |
struct node *lst3 = cons(1, lst2); |
printf("%d\n", lst3->rest->rest->first); |
} |
Note that this cons function can only construct lists of integers.
We can explain what the program is doing with the aid of the memory model.
Just before cons(5, NULL) returns:

Just before cons(3, lst1) returns:

Just before cons(1, lst2) returns:

C and C++ do not have automatic garbage collection the way Racket and Java do. A chunk of memory allocated by malloc stays allocated until it is recycled by calling free with its address as argument. We must write functions to recycle any allocated memory we no longer need.
void free_list(struct node *lst) { |
struct node *p; |
while (lst != NULL) { |
p = lst->rest; |
free(lst); |
lst = p; |
} |
} |
Here are some common memory management problems.
A memory leak: Failure to free memory no longer used.
A "dangling pointer": Using a pointer to or into a freed chunk of memory.
Calling free on a pointer not obtained through malloc.
Calling free more than once on the same pointer.
The address sanitizer can help catch many of these errors. To use it, add the -fsanitize=address flag to the compile command using clang. It is debatable whether this requirement (to not leak memory) should be imposed while learning, but our CS 136 course does this, and it makes sense to learn good habits early, rather than have to break bad habits later. So you might consider doing this.
A common debugging technique is to add printf statements to look at data values during the computation. But printf can only print primitive types. We must write functions to "show" our data structures. Here is an example for lists.
void print_list(struct node *lst) { |
struct node *p; |
printf("( "); |
for (p = lst; p != NULL; p = p->rest) |
printf("%d ", p->first); |
printf(")\n"); |
} |
Another helpful debugging aid is the ability to print pointers using the %p format specification in printf. The specific values are not that useful, but you can compare pointers for equality. GDB lets you examine the contents of memory in a more useful fashion.
As an example of a simple task involving list creation, consider copying an existing list. Here is Racket code to do this.
| (define (copy lst) |
| (cond |
| [(empty? lst) empty] |
| [else (cons (first lst) |
| (copy (rest lst)))])) |
Since lists are immutable in Racket, there is no reason to do this; we cannot distinguish the result of this function from its argument. But tracing the execution of an application of copy to a specific argument, in the memory model, will demonstrate that there is no sharing between the argument and the result. And this is a useful operation in C, where sharing is most definitely visible.
The above code is not tail-recursive, so translating it into C is non-trivial. I’ll use a common technique of maintaining a pointer to the previous node in a list (in this case, the previously-created node in the result).
struct node *copy(struct node *lst) { |
struct node *ans = NULL; |
struct node *prev; |
if (lst == NULL) return ans; |
|
ans = cons(lst->first, NULL); |
prev = ans; |
lst = lst->rest; |
|
while (lst != NULL) { |
prev->rest = cons(lst->first, NULL); |
prev = prev->rest; |
lst = lst->rest; |
} |
|
return ans; |
} |
Here is a more clever (though harder to understand) version of copy, which makes use of the "address-of" operator to eliminate the special case above.
struct node *copy2(struct node *lst) { |
struct node *ans = NULL; |
struct node **prevloc = &ans; |
while (lst != NULL) { |
struct node *new = cons(lst->first, NULL); |
*prevloc = new; |
prevloc = &new->rest; |
lst = lst->rest; |
} |
return ans; |
} |
3.5 List Exercises
struct node { |
int first; |
struct node *rest; |
} |
write a C function struct node *reverse(struct node *lst) which reverses the list (without allocating any new memory) and returns a pointer to the reversed list. Your code should not use recursion.
This is a standard technical question asked by job interviewers. (If this happens to you, and they don’t ask the question carefully enough, give them a purely-functional answer in Racket, it is much easier.)
You may wish to work out the ideas in Racket, using mutable pairs (section 3.10 of the Racket Reference). \(\blacksquare\)
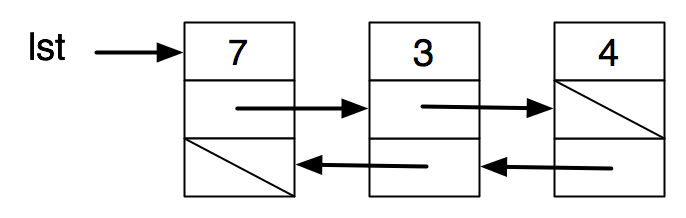
Exercise 5: The awkwardness of having to keep a "previous" pointer while doing list operations on a list such as defined in the previous exercise can be avoided by maintaining these pointers in the data structure itself.
struct node { |
int first; |
struct node *rest; |
struct node *prev; |
} |
Here is a box-and-pointer diagram of such a “doubly-linked” list.
Write the following C functions.
struct node *cons(int v, struct node *lst)
Adds the value v to the front of the list and returns a pointer to the resulting list.
void add_after(int v, struct node *nptr)
Adds the value v after the node pointed to by nptr (which cannot be NULL).
struct node *remove_first(struct node *lst, int key)
Removes the first occurrence of key in the list (or has no effect if that value does not appear in the list) and returns a pointer to the resulting list. \(\blacksquare\)
Exercise 6: This question asks you to write a C version of one of the programming questions in FICS.
To write C code implementing the immutable natural number ADT, we keep lists of bigits, or blists (where the least significant digit is first in the list) in the following structure:
struct node { |
int bigit; |
struct node *next; |
}; |
Your goal is to write and test these C functions:
void print_num(struct node *nlst); |
struct node *add(struct node *n1lst, struct node *n2lst); |
struct node *mult(struct node *n1lst, struct node *n2lst); |
print_num prints the number represented by nlst in human-readable form (as it would be printed by Racket; no spaces or newlines). You may use recursion for print_num. (How would you do it without using recursion, with the same asymptotic running time and using only \(O(1)\) space?)
Do not use recursion for add, mult, or any of their helper functions. Remember that this is an immutable ADT, so these functions produce a new value.
To aid in accomplishing these tasks, write the following utility functions.
struct node *cons_bigit(int bgt, struct node *nxt); |
void free_num(struct node *blst); |
struct node *copy_num(struct node *nlst); |
cons_bigit adds the bigit bgt to the front of the blist pointed to by nxt. For example, the following code creates the blist representing 1234567890.
struct node *n = cons_bigit(7890, cons_bigit(3456, cons_bigit(12, NULL))); |
copy_num makes a completely separate copy of blst.
free_num frees all the memory used by the blist pointed to by blst.
For maximum learning benefit, use the address sanitizer as explained above to ensure that all memory that you allocate actually gets freed.
You may find that going from recursive code for add in Racket to non-recursive code for add in C is a big leap. In this case, you should consider writing add_rec, a recursive version in C, as an intermediate step. \(\blacksquare\)
Here are some remarks on exercise 6.
For the C code for this exercise, and for subsequent exercises, you should use those aspects of the design recipe from HtDP or FICS that are still relevant. You are writing this code for your own benefit, not for submission to an instructor or employer, but it is good practice for those situations.
You need not write contracts, since function prototypes provide that information, but you should create a comment header for each function giving its purpose in a fashion that makes clear the role of each parameter, a description of any side effects (both mutation and printing), and an example of use. You should test utility and helper functions before testing the functions that use them, and you should write your tests in a directed fashion, so that it is clear for each test what it is testing, and every line of code is exercised.
C code typically requires more documentation than Racket code, and you can use single-line comments in the code to help clarify your intent.
This choice of base avoids arithmetic overflow, but wastes space in each bigit. This means that the lists representing numbers are longer than they need to be, and the operations consequently slower (both by some constant factor). With knowledge of the full range of integer types and operations provided by C, this can be avoided, and the code made more efficient in both time and space.
Both Racket (and Scheme) implementations and libraries that provide "bignum" capability to languages that lack primitive unbounded numbers tend to use different techniques than the ones listed here. The full flexibility of lists is not needed for bignums, and typically bigits (a term made up for these exercises) are stored in consecutive memory locations (like arrays). This also avoids the awkward tradeoffs revealed by print_num. You can learn more than you ever wanted to know about the issues involved in such implementations by perusing the documentation of the open-source GNU GMP library.
3.6 Queues
FICS covers queues in Racket, both using mutation (in a fashion very similar to what I do below in C) and a purely functional implementation. FDS has a whole chapter on various implementations.
Efficient access to lists follows a last-in, first-out pattern. If we want to add an element to the end of a list, it takes time roughly proportional to the length of the list.
In the data structure called a queue, items are added at the end and removed from the front, resulting in a first-in, first-out pattern.
I will define the mutable queue ADT, and provide an implementation.
Mathematically, a queue is a (possibly empty) sequence \(q_1, q_2, \ldots, q_n\).
Here are the associated operations:
enqueue: two parameters, an item \(e\) and a queue \(Q = q_1, q_2, \ldots, q_n\); precondition true; postcondition is \(Q = q_1, q_2, \ldots, q_n, e\); no value produced.
dequeue: one parameter, a queue \(Q = q_1, q_2, \ldots, q_n\); precondition \(n \ge 1\); value produced is \(q_1\); postcondition is \(Q = q_2, \ldots, q_n\).
empty-queue: one parameter, a queue \(Q = q_1, q_2, \ldots, q_n\); precondition “true”; value produced is “true” iff \(n=0\); postcondition is that \(Q\) is unchanged.
Here is an implementation, using lists together with a struct that provides pointers both to the first element of the list (typical) but also to the last element of the list (for fast addition to the end of the list).
struct node { |
int first; |
struct node *rest; |
}; |
|
struct queue { |
struct node *head; |
struct node *tail; |
}; |
|
struct queue *new_queue(void) { |
struct queue *ans; |
ans = malloc(sizeof(struct queue)); |
if (ans == NULL) { |
printf("out of memory\n"); |
abort(); |
} |
ans->head = NULL; |
ans->tail = NULL; |
return ans; |
} |
|
void enqueue(struct queue *q, int item) { |
struct node *newnode; |
newnode = cons(item, NULL); |
if (q->head == NULL) { |
q->head = newnode; |
} else { |
q->tail->rest = newnode; |
} |
q->tail = newnode; |
} |
|
int dequeue(struct queue *q) { |
int ans; |
struct node *oldnode; |
oldnode = q->head; |
ans = oldnode->first; |
q->head = q->head->rest; |
free(oldnode); |
return ans; |
} |
This implementation makes heavy use of mutation to ensure \(O(1)\) running time for all operations.
3.7 Arrays
The C equivalent of a Racket vector is called an array. The array is a central data structure in C, unlike vectors in Racket.
The C statement int a[5]; declares an array a of five integers. These occupy five consecutive words in memory. For a local declaration in a function, those five words will be in the stack frame.
As with Racket, indices start at 0, and array references in C take \(O(1)\) time. Unlike with Racket, there is no way to compute the length of an array at run time. In C99, the size of a declared array can (with certain restrictions) be a computed expression.
The name of the element of a of index 4 is a[4]. This works as an lvalue and as an rvalue.
int a[5]; |
... |
j = a[4]; |
a[4] = k + 1; |
Important point:
unlike in Racket or Java,
a compiled C program does not check
if an array index is between 0 and the length of the array minus 1.
We could have used a[5] as a reference, or even
a[-3].
Here is a function to sum up the elements of an array.
int sum(int A[], int len) { |
int ans = 0; |
for (int i=0; i<len; i++) { |
ans = ans + A[i]; |
} |
return ans; |
} |
Notice that because there is no way to determine the length of an array in C, the length must be provided to this function as a separate parameter.
The following program demonstrates another possible source of error.
int main(void) { |
int A[10] = {0}; |
printf("%d\n", A[100]); |
printf("%d\n", A[1000000000]); |
Note the initialization of all elements of the array A. If we compile and run this program, the second printf statement is likely to produce a segmentation fault. The first printf statement will probably not cause the program to crash, but it is likely to print some unpredictable value.
Consider the following array (note the lack of an explicit length in the declaration; because of the initialization provided, the compiler can figure it out):
int b[] = {9, 2, 5, 1, 12};
Here is how it is represented in the memory model:
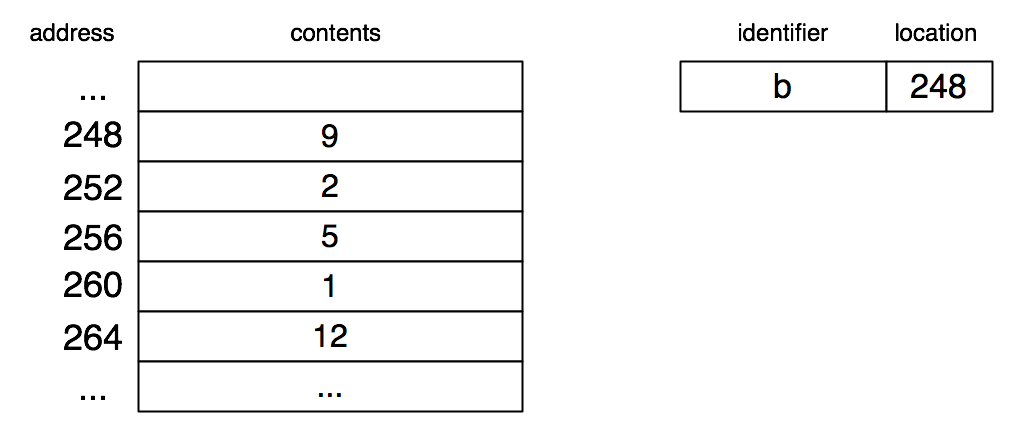
To compute the address of the element of index i, we simply multiply i by 4 and add 248 (in this case). This is what the compiled code would do to access b[i].
3.8 Dynamic allocation of arrays
int *b; |
b = malloc(5 * sizeof(int)); |
b[0] = 9; |
The memory picture resembles that of the previous example, except that the five words of the array are allocated on the heap.
*b and b[0] mean the same thing, as lvalues and as rvalues. We can use b anywhere an integer array parameter is used, for example, in the call sum(b,1).
Sometimes you might want to resize a dynamically-allocated array. The realloc function will try to do this. If the memory right after the array is available for use, the adjustment is simple and takes constant time. Otherwise realloc must find a large enough block, copy over the current contents of the array, and produce a pointer to the new location.
This will take \(O(n)\) time on an array of size \(n\). You should avoid using realloc unless you’re willing to pay the possible time penalty (and account for it in worst-case analysis). It is only mentioned here because one of the textbooks mentions it, and I have noticed students using the less desirable Approach 2 below.
Example: reading numbers into an array.
Approach 1: Guess the needed size.
int numbers[50]; |
int nextindex = 0; |
while (has_next()) { |
if (nextindex == 50) abort(); |
numbers[nextindex] = read_nat(); |
nextindex++; |
} |
As you can imagine, this does not work very well if the guess is too small.
Approach 2: Grow incrementally.
int size = 50; |
int *numbers = malloc(size * sizeof(int)); // should check |
int nextindex = 0; |
while (has_next()) { |
if (nextindex == size) { |
size++; |
numbers = realloc(numbers, size * sizeof(int)); // should check |
} |
numbers[nextindex] = read_nat(); |
nextindex++; |
} |
This works, but takes \(O(N^2)\) time for \(N\) input numbers, because it potentially does \(O(N)\) work each time through the loop.
Approach 3: Double up.
int size = 50; |
int *numbers = malloc(size * sizeof(int)); //should check |
int nextindex = 0; |
while (has_next()) { |
if (nextindex == size) { |
size *= 2; |
numbers = realloc(numbers, size * sizeof(int)); //should check |
} |
numbers[nextindex] = read_nat(); |
nextindex++; |
} |
This takes \(O(N)\) time for \(N\) input numbers. Suppose the final size is \(50\cdot 2^k\). This has to be less than twice \(N\). Then the total cost of using realloc is proportional to the sum of the sizes of each copy done by realloc, which is \(50+100+\ldots+50\cdot 2^k\), bounded above by \(4N\).
As examples of the idiomatic use of arrays in C, we will consider a couple of sorting algorithms. First, insertion sort. Here’s how it looks in HtDP and FICS.
| (define (isort alon) |
| (cond |
| [(empty? alon) empty] |
| [else (insert (first alon) (isort (rest alon)))])) |
| (define (insert n alon) |
| (cond |
| [(empty? alon) (cons n empty)] |
| [(<= n (first alon)) (cons n alon)] |
| [else (cons (first alon) (insert n (rest alon)))])) |
We’ll try something similar with C arrays. We now know that each use of cons in the Scheme code allocates a new cons cell on the heap. "Forgotten" cells are garbage-collected. To avoid this overhead in the C code, we will do the computation using mutation on the array holding the data, rearranging values to produce the answer.
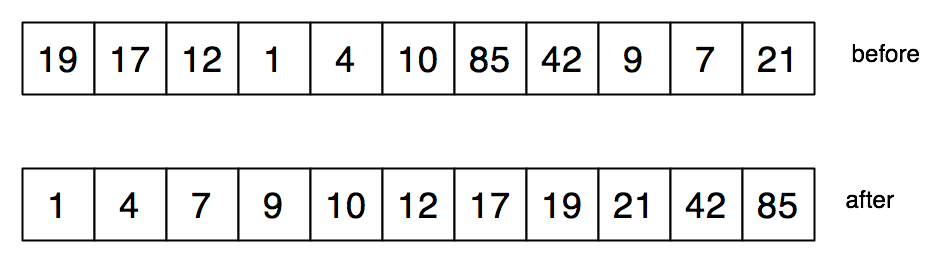
We will also use loops instead of recursion. This is tricky, as neither isort nor insert is tail-recursive.
Our C code will insert the \(i\)th element of the array into the array segment consisting of the original elements of index \(i+1, i+2, \ldots n-1\), rearranged to be in nondecreasing order.
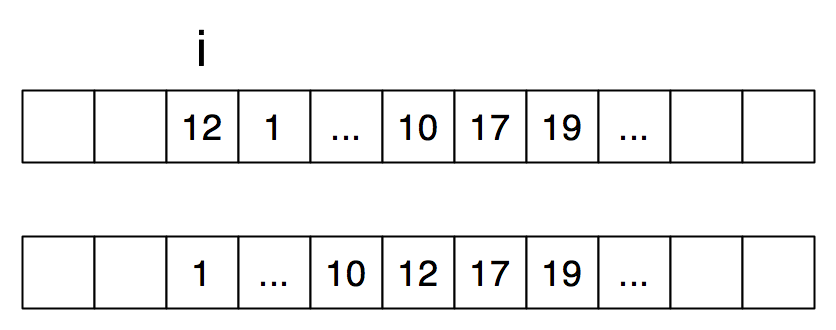
Before and after this operation, the data occupies elements \(i\) through \(n-1\) of the array. The computation rearranges elements in place. The next code fragment moves back elements in the already sorted portion, one by one, until there is a hole at the right spot for what used to be the \(i\)th element.
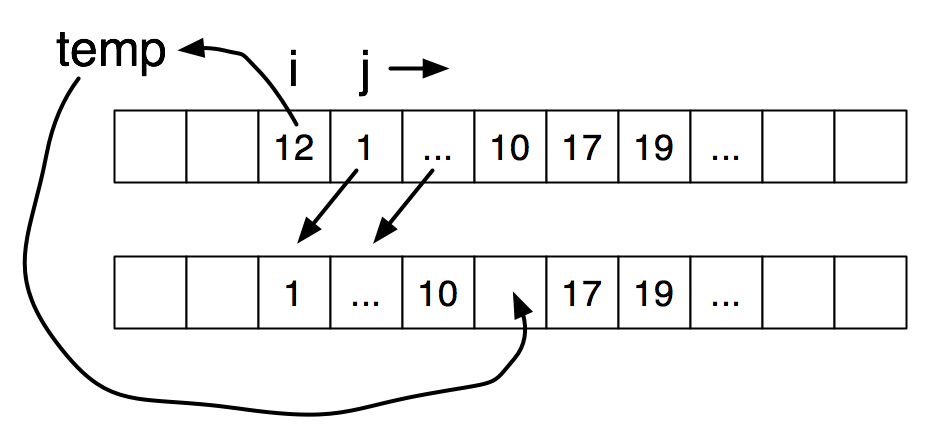
int j, temp; |
temp = A[i]; |
for (j=i+1; j < n; j++) { |
if (A[j] < temp) { |
A[j-1] = A[j]; |
} |
else break; |
} |
A[j-1] = temp; |
We can now put this into an
insert helper function.
void insert(int i, int A[], int n) { |
int j, temp; |
temp = A[i]; |
for (j=i+1; j < n; j++) { |
if (A[j] < temp) { |
A[j-1] = A[j]; |
} |
else break; |
} |
A[j-1] = temp; |
} |
|
const int N = 5; // C99 alternative to #define N 5 |
|
int main(void) { |
int i, B[N]; |
printf("Enter %d numbers: ",N); |
for (i = 0; i < N ; i++) { |
scanf("%d",&B[i]); |
} |
for (i = N-2; i >= 0; i--) { |
insert(i,B,N); |
} |
printf("Sorted numbers are: "); |
for (i = 0; i < N; i++) { |
printf("%d ", B[i]); |
} |
printf("\n"); |
return 0; |
} |

We can "inline" the definition of insert to do the sorting within one function.
void isort(int A[], int n) { |
int i, j; |
for (i = n-2; i >= 0; i--) { |
int temp = A[i]; |
for (j=i+1; j < n; j++) { |
if (A[j] < temp) { |
A[j-1] = A[j]; |
} |
else break; |
} |
A[j-1] = temp; |
} |
} |
This version of insertion sort, like the Racket version with a list argument, has \(O(n^2)\) running time.
Next, we will consider an algorithm called selection sort that does not have a natural Racket list implementation. Selection sort finds the smallest item and moves it to index 0, then moves the smallest item in the rest of the array to index 1, and so on.
void ssort(int A[], int n) { |
int i, j; |
for (i = 0; i < N-1; i++) { |
int min = A[i]; // find min |
int min_i = i; |
for (j=i+1; j < N; j++) { |
if (A[j] < min) { |
min = A[j]; |
min_i = j; |
} |
} |
int temp = A[min_i]; // swap |
A[min_i] = A[i]; |
A[i] = temp; |
} |
} |
As I said earlier, vectors are not used much in Racket, but they are used a lot in C. Here are two different perspectives on the matter.
Vectors are inflexible
Vectors tend to encourage mutation
There aren’t abstract vector functions
If you’re processing items in order, you might as well use a list
Array declaration and manipulation in C requires less code than lists in C
Arrays are also faster and use less memory
It is not the case that one of these perspectives is right and the other wrong. We should use the right data structure for a given task, tempered by language considerations.