7 Efficient Representations
\(\newcommand{\la}{\lambda} \newcommand{\Ga}{\Gamma} \newcommand{\ra}{\rightarrow} \newcommand{\Ra}{\Rightarrow} \newcommand{\La}{\Leftarrow} \newcommand{\tl}{\triangleleft} \newcommand{\ir}[3]{\displaystyle\frac{#2}{#3}~{\textstyle #1}}\)
Let’s return to the simulation of natural numbers by Racket structures that we developed in the chapter on structures. Our goal is to improve the efficiency of this simulation, and to derive the method used to actually represent natural numbers and integers in a modern digital computer.
Here we have a difference in the perspectives of mathematics and computer science. Mathematically, our simulation is correct, and its simplicity facilitates proofs. Computationally, our simulation is not efficient enough, and we will trade some simplicity for better efficiency.
We’ll start with a review of our earlier work.
7.1 Unary representation reviewed
| (define-struct Z ()) |
| (define-struct S (pred)) |
Data definition: a Nat is either (make-Z) or it is (make-S p), where p is a Nat.
(make-Z) represents \(0\); (make-S p) represents \(n+1\), where p is a Nat representing \(n\).
We will now call this definition the unary definition of Nat, because we will shortly introduce another one.
The unary representation of the natural number 3 is (make-S (make-S (make-S (make-Z)))). Imagine the unary representation of 1000000 (one million). It probably wouldn’t fit in your browser window as you are reading this (unless you have a huge screen with incredible resolution, and really good eyes). Intuitively speaking, this means it takes up a lot of space in the memory of a computer.
Recall our implementation of addition.
| (define (plus nat1 nat2) |
| (cond |
| [(Z? nat1) nat2] |
| [(S? nat1) (make-S (plus (S-pred nat1) nat2))])) |
Imagine how many steps would be in the trace if we added the representations of 1000000 and 1. Intuitively, we can do much better in our heads, so we might be able to in our code.
We could try to interpret make-S as something other than "successor". So (make-S (make-Z)) could be a number different from one.

But consider the representation of the first million natural numbers. Even though each of them can be represented with at most six decimal digits, one of those numbers has to have a long representation in unary, regardless of how we interpret make-S.
Since we are familiar with decimal notation, our first inclination might be to just try to use that. Earlier, I asked you to imagine writing down a precise definition of addition as you knew it before you started reading this flânerie, in contrast with the simplicity of the definition of plus above. There might be notation which is computationally only slightly more complicated than unary, but which brings us the benefit of efficiency.
The bottleneck is that, so far, we have only one data constructor, make-S, that can be applied to an existing Nat to create a new one. The simplest change we can make is to use two data constructors of this type.
7.2 Binary representation introduced
Here are the structures we’ll use.
| (define-struct Z ()) |
| (define-struct A (way)) |
| (define-struct B (gone)) |
Unlike with the unary definition, there is no significance to the names A and B, and the names of the fields are chosen to make weak puns on the idea of "removing a constructor".

Every natural number should be representable. None should be left out.
The representation should be unique. Each natural number should have exactly one representation.
Computation using the representation should be relatively straightforward and efficient.
It would be nice if there were a natural interpretation of the representation, and if small numbers had a small representation.
If we have a set of values constructed with these structures, and we add an make-A constructor to each one, and also separately add a make-B constructor to each one, we will have doubled the number of values represented. This suggests that the interpretation of adding one of these constructors should have something to do with doubling the value represented. We could choose the interpretation of make-A to be "double the value". That is, if v is the representation of the natural number \(n\), then (make-A v) will be the representation of \(2n\). This can only produce even numbers; the odd numbers are left out. So the make-B constructor has to take care of those. We choose the interpretation of make-B to be "double the value, then add one". So if v is the representation of the natural number \(n\), then (make-B v) will be the representation of \(2n+1\).
We immediately run into a problem: the representation is not unique. Both (make-Z) and (make-A (make-Z)) represent 0. In fact, so does (make-A (make-A (make-Z))). We can avoid this issue by disallowing this in the data definition. We won’t let make-A be applied to a (make-Z). Here is the binary definition of Nat.
Data definition: A Nat is either (make-Z), or it is (make-A p) where p is a Nat that is not (make-Z), or it is (make-B p), where p is a Nat.
This is a bit awkward. We could use an interpretation which doesn’t require a special rule like this, but it wouldn’t be as natural. You might think about this, as it will come up later.
Here are the binary Nat representations of the first few natural numbers.
\(0\) is (make-Z).
\(1\) is (make-B (make-Z)).
\(2\) is (make-A (make-B (make-Z))).
\(3\) is (make-B (make-B (make-Z))).
\(4\) is (make-A (make-A (make-B (make-Z)))).
\(5\) is (make-B (make-A (make-B (make-Z)))).
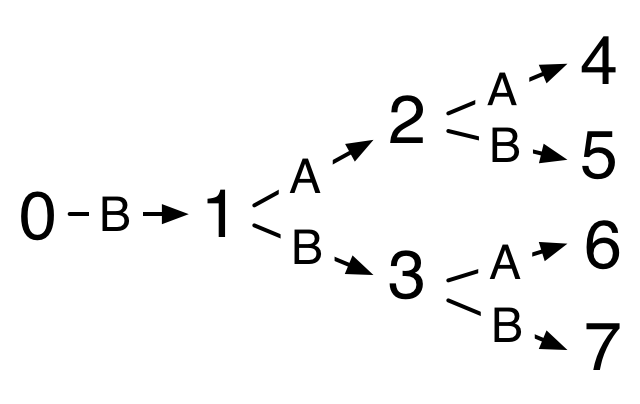
Every natural number has a unique representation as a binary Nat. You might think about how to prove this. On a more computational level, using the data definition, we can derive a template for recursion on binary Nats.
| (define (my-nat-fn nat) |
| (cond |
| [(Z? nat) ...] |
| [(A? nat) ...] |
| [(B? nat) ...])) |
| (define (my-nat-fn nat) |
| (cond |
| [(Z? nat) ...] |
| [(A? nat) ... (my-nat-fn (A-way nat)) ...] |
| [(B? nat) ... (my-nat-fn (B-gone nat)) ...])) |
As an example of its use, consider converting a binary Nat to the built-in Racket number it represents. This is a straightforward application of the interpretation.
| (define (from-Nat nat) |
| (cond |
| [(Z? nat) 0] |
| [(A? nat) (* 2 (from-Nat (A-way nat)))] |
| [(B? nat) (add1 (* 2 (from-Nat (B-gone nat))))])) |
To convert in the other direction, we have to invert the interpretation. We already noted that applying make-A results in the representation of an even number, and it’s clear that applying make-B results in the representation of an odd number, since our interpretation of it is "double the value, then add one". This suggests the following case analysis.
| (define (to-Nat k) |
| (cond |
| [(zero? k) ...] |
| [(even? k) ...] |
| [(odd? k) ...])) |
If \(k\) is even, then its representation is make-A applied to the representation of half of \(k\). Reasoning like this allows us to complete the code.
| (define (to-Nat k) |
| (cond |
| [(zero? k) (make-Z)] |
| [(even? k) (make-A (to-Nat (/ k 2)))] |
| [(odd? k) (make-B (to-Nat (/ (sub1 k) 2)))])) |
Racket’s predefined quotient function (which performs integer division) does the calculation nicely for us.
| (define (to-Nat k) |
| (cond |
| [(zero? k) (make-Z)] |
| [(even? k) (make-A (to-Nat (quotient k 2)))] |
| [(odd? k) (make-B (to-Nat (quotient k 2)))])) |
You might worry that we are hiding inefficiencies in the use of the predefined functions. But, in fact, Racket is internally using a variation of the very representation we have developed. So the predefined functions used here are no more difficult to compute than the structure type predicates and accessors we used in from-Nat. By the end of the second part of this flânerie, you will learn more details about this.
7.3 Implementing addition
Let’s work on implementing addition for binary Nats, starting again with the template.
| (define (my-nat-fn nat) |
| (cond |
| [(Z? nat) ...] |
| [(A? nat) ... (my-nat-fn (A-way nat)) ...] |
| [(B? nat) ... (my-nat-fn (B-gone nat)) ...])) |
| (define (plus nat1 nat2) |
| (cond |
| [(Z? nat1) nat2] |
| [(A? nat1) ... (plus (A-way nat1) nat2) ...] |
| [(B? nat1) ... (plus (B-gone nat1) nat2) ...])) |
If nat1 represents \(2x\) and nat2 represents \(y\), then (A-way nat1) represents \(x\). What does \(x+y\) tell us about \(2x+y\)? Not enough. We’re not going to be able to do this with structural recursion on one parameter, as we managed with the unary representation. Let’s try using structural recursion on two binary Nats.
| (define (my-nat-fn nat1 nat2) |
| (cond |
| [(Z? nat1) ...] |
| [(Z? nat2) ...] |
| [(and (A? nat1) (A? nat2)) |
| ... (my-nat-fn (A-way nat1) (A-way nat2))] |
| [(and (A? nat1) (B? nat2)) |
| ... (my-nat-fn (A-way nat1) (B-gone nat2))] |
| [(and (B? nat1) (A? nat2)) |
| ... (my-nat-fn (B-gone nat1) (A-way nat2))] |
| [(and (B? nat1) (B? nat2)) |
| ... (my-nat-fn (B-gone nat1) (B-gone nat2))])) |
The first couple of cases are easy.
| (define (plus nat1 nat2) |
| (cond |
| [(Z? nat1) nat2] |
| [(Z? nat2) nat1] |
| [(and (A? nat1) (A? nat2)) ... (plus (A-way nat1) (A-way nat2))] |
| [(and (A? nat1) (B? nat2)) ... (plus (A-way nat1) (B-gone nat2))] |
| [(and (B? nat1) (A? nat2)) ... (plus (B-gone nat1) (A-way nat2))] |
| [(and (B? nat1) (B? nat2)) ... (plus (B-gone nat1) (B-gone nat2))])) |
In the first unfinished case, if nat1 represents \(2x\) and nat2 represents \(2y\), then (A-way nat1) represents \(x\) and (B-gone nat2) represents \(y\). The sum we want, \(2x+2y\), is twice \(x+y\) (the result of the recursive application). We can get this by applying make-A to the result. But remember we have a restriction on the use of make-A. Can the result be (make-Z)? No, because (A-way nat1) can’t be (make-Z), if nat1 is a properly-formed binary Nat.
Similar reasoning lets us finish the next two cases as well.
| (define (plus nat1 nat2) |
| (cond |
| [(Z? nat1) nat2] |
| [(Z? nat2) nat1] |
| [(and (A? nat1) (A? nat2)) |
| (make-A (plus (A-way nat1) (A-way nat2)))] |
| [(and (A? nat1) (B? nat2)) |
| (make-B (plus (A-way nat1) (B-gone nat2)))] |
| [(and (B? nat1) (A? nat2)) |
| (make-B (plus (B-gone nat1) (A-way nat2)))] |
| [(and (B? nat1) (B? nat2)) |
| ... (plus (B-gone nat1) (B-gone nat2)) ...])) |
The last case is a bit trickier. If nat1 represents \(2x+1\) and nat2 represents \(2y+1\), then the result of the recursive application represents \(x+y\). But the answer is the representation of \(2x+2y+2\). We can’t get this just by putting one constructor on the result of the recursive application. The solution is to define a plus-one helper function, which uses structural recursion for binary Nats on its single parameter.
| (define (plus nat1 nat2) |
| (cond |
| [(Z? nat1) nat2] |
| [(Z? nat2) nat1] |
| [(and (A? nat1) (A? nat2)) |
| (make-A (plus (A-way nat1) (A-way nat2)))] |
| [(and (A? nat1) (B? nat2)) |
| (make-B (plus (A-way nat1) (B-gone nat2)))] |
| [(and (B? nat1) (A? nat2)) |
| (make-B (plus (B-gone nat1) (A-way nat2)))] |
| [(and (B? nat1) (B? nat2)) |
| (make-A (plus-one (plus (B-gone nat1) (B-gone nat2))))])) |
| (define (plus-one nat) |
| (cond |
| [(Z? nat) (make-B (make-Z))] |
| [(A? nat) (make-B (A-way nat))] |
| [(B? nat) (make-A (plus-one (B-gone nat)))])) |
One of our criteria for the representation was that it should be "natural". Is it?
\(4\) is represented by (make-A (make-A (make-B (make-Z)))). To see the correspondence with a more natural interpretation, erase the parentheses and make-Z, replace each make-A with 0 and each make-B with 1, and reverse the resulting sequence of digits. The result is 100. But this is not one hundred.
\(4 = 1 \times 2^2 + 0\times 2^1 + 0\times 2^0\)
\(4=100_2\) (one hundred in base two).
This is known as binary notation. A binary digit (0 or 1) is often called a bit. The rule that we don’t apply make-A to (make-Z) corresponds to the convention of not writing leading zeroes on numbers (whether using binary notation or decimal notation).
Binary notation is used to represent natural numbers in computers. The two different bits 0 and 1 can be represented by two different voltage levels. Eight bits are typically grouped into a byte, and four bytes into a 32-bit or 64-bit word.
A 32-bit word representing the natural number 4 would be filled with zeroes on the left:
00000000000000000000000000000100
Why is binary used in computers and not decimal? The code we have developed for binary addition is implemented in hardware. Our code essentially uses the addition table for binary digits.
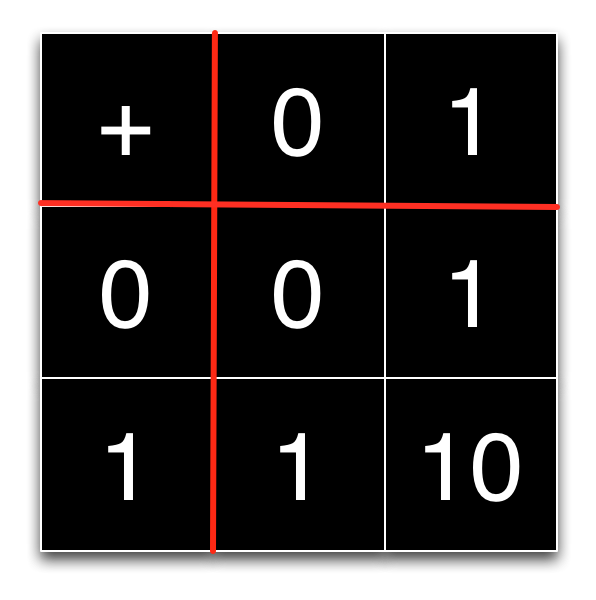
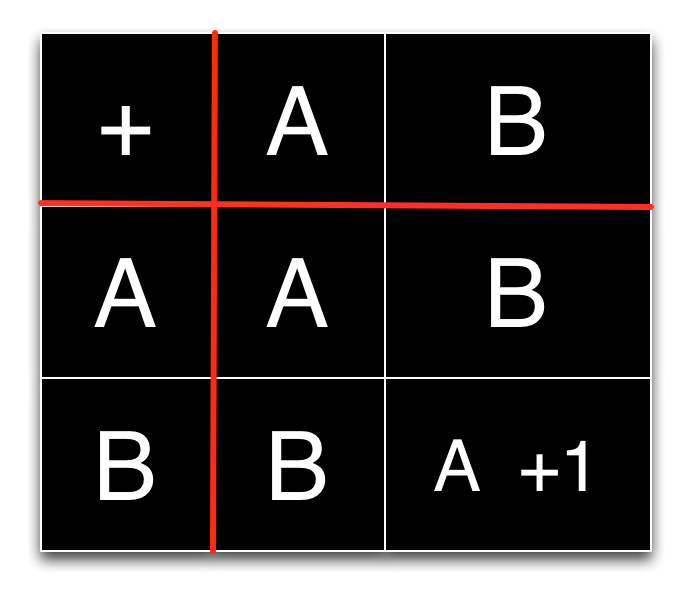
The correspondence between the binary addition table and our algorithm becomes clearer if we rewrite the table slightly.
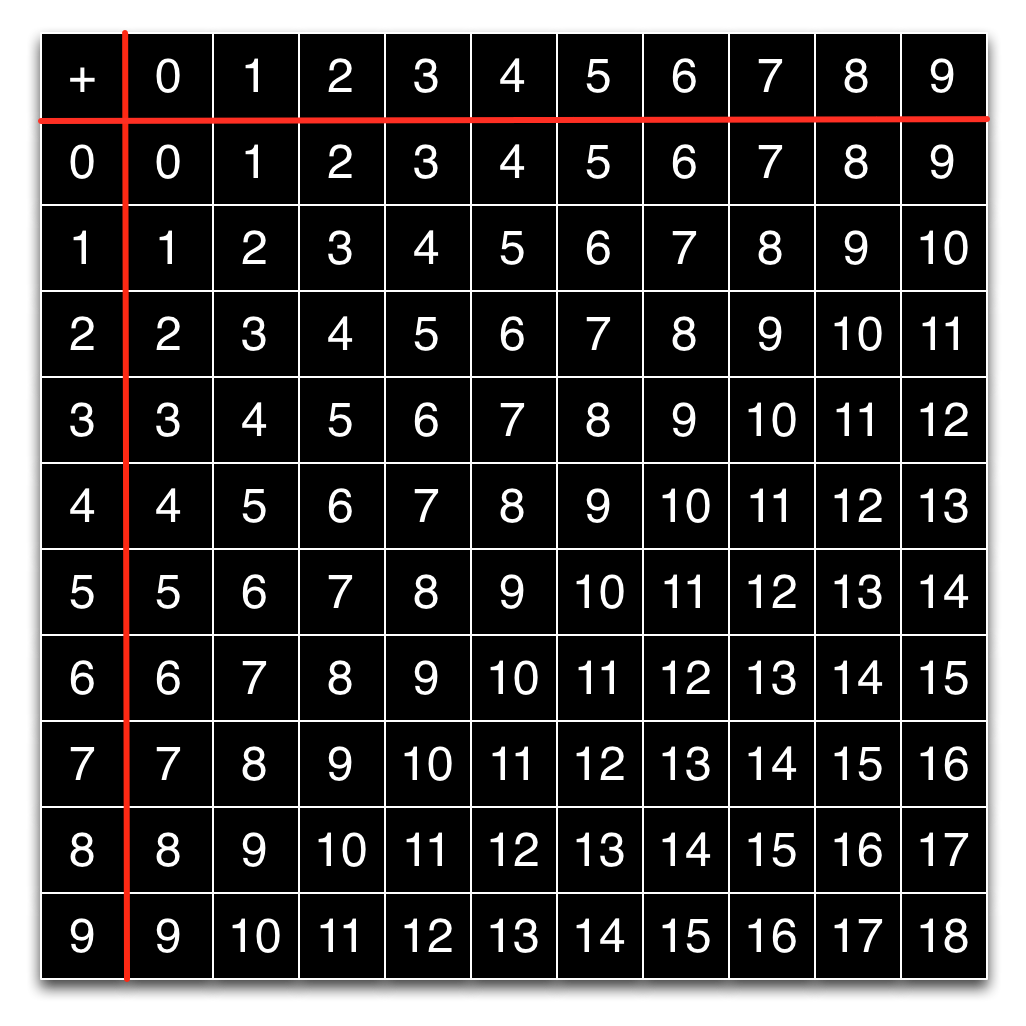
In contrast, the addition table for decimal digits is much larger, and would lead to more complex hardware.
7.4 Space and time analysis
We do not have a proper model of space or memory use. For the time being, we’ll take the number of constructors used in a Nat as a measure of memory use. This is easy to compute, should we need to do that.
| (define (size nat) |
| (cond |
| [(Z? nat) 1] |
| [(A? nat) (add1 (size (A-way nat)))] |
| [(B? nat) (add1 (size (B-gone nat)))])) |
Let’s define \(S(n)\) as (size nat), where nat is the binary representation of \(n\). We’re interested in how quickly \(S(n)\) grows.
\(n~~~\) |
| nat |
| \(S(n)\) |
\(0\) |
| (make-Z) |
| \(1\) |
\(1\) |
| (make-B (make-Z)) |
| \(2\) |
\(2\) |
| (make-A (make-B (make-Z))) |
| \(3\) |
\(3\) |
| (make-B (make-B (make-Z))) |
| \(3\) |
\(4\) |
| (make-A (make-A (make-B (make-Z)))) |
| \(4\) |
\(5\) |
| (make-B (make-A (make-B (make-Z)))) |
| \(4\) |
\(6\) |
| (make-A (make-B (make-B (make-Z)))) |
| \(4\) |
\(7\) |
| (make-B (make-B (make-B (make-Z)))) |
| \(4\) |
The pattern should be clear; the question is how to describe it mathematically.
Conjecture: For \(2^k \le n < 2^{k+1}\), \(S(n)=k+2\).
Or: For \(k \le \log_2 n < k+1\), \(S(n)=k+2\).
Or: For \(n>0\), \(S(n)=\lfloor\log_2 n\rfloor +2\).
In this last expression, the unusual brackets or "floors" refer to the "largest integer less than or equal to" function. The point is that \(S(n)\) grows approximately as the logarithm of \(n\). These conjectures can be proved by mathematical induction.
Next, we analyze the plus-one function.
| (define (plus-one nat) |
| (cond |
| [(Z? nat) (make-B (make-Z))] |
| [(A? nat) (make-B (A-way nat))] |
| [(B? nat) (make-A (plus-one (B-gone nat)))])) |
The recursive application of plus-one is on an argument whose size is one smaller than nat. Thus the number of applications of plus-one starting with an argument nat is bounded above by (size nat).
Our implementation of plus also reduces the size of its arguments in a similar fashion, but the last case is problematic:
| [(and (B? nat1) (B? nat2)) |
| (make-A (plus-one (plus (B-gone nat1) (B-gone nat2))))] |
The problem is accounting for the additional work done by plus-one. This case does not necessarily always happen, and when it does, it is not clear what the cost is, because plus-one itself does not always do a recursive application (it happens in only one of the three cases in its code). The code we developed is actually efficient, but justifying that is more complicated than I want for this exposition.
Instead, we will rewrite the code to make the analysis clearer. In place of using plus-one, we will develop a helper function plus-s, which computes the successor of the sum of its two arguments.
| [(and (B? nat1) (B? nat2)) |
| (make-A (plus-s (B-gone nat1) (B-gone nat2)))] |
plus has recursive applications of itself, and an application of plus-s. It will turn out that plus-s has recursive applications of itself, and applications of plus. plus and plus-s will be mutually recursive. The code for plus-s can be developed using the same kind of reasoning as for plus.
| (define (plus-s nat1 nat2) |
| (cond |
| [(Z? nat1) (plus-one nat2)] |
| [(Z? nat2) (plus-one nat1)] |
| [(and (A? nat1) (A? nat2)) |
| (make-B (plus (A-way nat1) (A-way nat2)))] |
| [(and (A? nat1) (B? nat2)) |
| (make-A (plus-s (A-way nat1) (B-gone nat2)))] |
| [(and (B? nat1) (A? nat2)) |
| (make-A (plus-s (B-gone nat1) (A-way nat2)))] |
| [(and (B? nat1) (B? nat2)) |
| (make-B (plus-s (B-gone nat1) (B-gone nat2)))])) |
The mutually-recursive plus and plus-s always reduce the size of their arguments in recursive applications. When one argument becomes (make-Z) (size one), plus-one may be used, and this reduces the size of its argument in recursive applications. Thus the total number of applications of plus, plus-s, and plus-one starting with arguments nat1 and nat2 is bounded above by the maximum of the sizes of nat1 and nat2.
Something similar is true of the number of applications of plus and plus-one in our original code, but the reasoning involved is more complicated. This matches our intuition that the work done in adding two numbers should be proportional to the number of digits, not the value of the numbers (as it was for the unary definition of Nat).
7.5 Representing integers
Let’s try to extend our efficient representation of natural numbers to an efficient representation of integers. Our first attempt will not work so well, and we’ll have to move to a different idea. First, we will try to augment with a sign, as we do with decimal numbers. We can view \(-8\) as a negative sign attached to the natural number \(8\).
| (define-struct Pos (nat)) |
| (define-struct Neg (nat)) |
Data definition: an Int is either a (make-Pos n) or a (make-Neg n), where n is a Nat.
Our first problem is that (make-Pos (make-Z)) and
(make-Neg (make-Z)) both represent the integer \(0\).
We solve this problem for decimal numbers by not writing \(-0\).
We can similarly forbid (make-Neg (make-Z)).
A bigger problem arises when we try to implement addition.
Some cases are easy.
| (define (iplus int1 int2) |
| (cond |
| [(and (Pos? int1) (Pos? int2)) |
| (make-Pos (plus (Pos-nat int1) (Pos-nat int2)))] |
| [(and (Pos? int1) (Neg? int2)) |
| ???] |
| ...)) |
Think about how we add a positive integer to a negative integer on paper. This is too complicated. Instead of augmenting with a sign, we will augment the structures we had for Nat with a new structure to represent the quantity \(-1\).
(define-struct N ())
Data definition: an Int is either (make-Z), or (make-N),
or (make-A p) or (make-B p), where p is an Int.
We keep the same interpretation of make-A and make-B.
(make-Z) represents \(0\).
(make-N) represents \(-1\).
(make-A p) represents \(2i\), where p represents \(i\).
(make-B p) represents \(2i+1\), where p represents \(i\).
An immediate advantage is that our representation of non-negative integers (natural numbers) is the same in Int as it is in Nat. All our code for plus is still useful. We only have to add cases that involve (make-N).
We still have the rule that we can’t apply make-A to (make-Z). But now we have the problem that (make-B (make-N)) and (make-N) both represent \(-1\). So we must add the rule that we can’t apply make-B to (make-N).
One way to enforce these rules is to create smart constructors, which are replacements for make-A and make-B with the rules built in. But these go beyond guarded constructors as seen earlier, because instead of raising errors, they provide a meaningful answer. So, for example, we can use the smart constructor replacing make-A to multiply all integers by 2.
| (define (sA int) |
| (cond |
| [(Z? int) int] |
| [else (make-A int)])) |
| (define (sB int) |
| (cond |
| [(N? int) int] |
| [else (make-B int)])) |
As before, we define \(S(i)\) to be the number of constructors in the representation of \(i\).
\(i~~~\) |
| nat |
| \(S(i)\) |
\(0\) |
| (make-Z) |
| \(1\) |
\(-1\) |
| (make-N) |
| \(2\) |
\(-2\) |
| (make-A (make-N)) |
| \(2\) |
\(-3\) |
| (make-B (make-A (make-N))) |
| \(3\) |
\(-4\) |
| (make-A (make-A (make-N))) |
| \(3\) |
\(-5\) |
| (make-B (make-B (make-A (make-N)))) |
| \(4\) |
\(-6\) |
| (make-A (make-B (make-A (make-N)))) |
| \(4\) |
\(-7\) |
| (make-B (make-A (make-A (make-N)))) |
| \(4\) |
\(-8\) |
| (make-A (make-A (make-A (make-A)))) |
| \(4\) |
To implement addition for binary Ints, all we need to do is add the missing cases.
| (define (plus int1 int2) |
| (cond |
| [(Z? int1) int2] |
| [(Z? int2) int1] |
| ; add N cases here |
| [(and (A? int1) (A? int2)) |
| (sA (plus (A-way int1) (A-way int2)))] |
| [(and (A? int1) (B? int2)) |
| (sB (plus (A-way int1) (B-gone int2)))] |
| [(and (B? int1) (A? int2)) |
| (sB (plus (B-gone int1) (A-way int2)))] |
| [(and (B? int1) (B? int2)) |
| (sA (plus-one (plus (B-gone int1) (B-gone int2))))])) |
| (define (plus-one int) |
| (cond |
| [(Z? int) (sB (make-Z))] |
| ; add N case here |
| [(A? int) (sB (A-way int))] |
| [(B? int) (sA (plus-one (B-gone int)))])) |
Here are the missing cases.
| ; missing cases for plus |
| [(and (N? int1) (N? int2)) (sA (make-N))] |
| [(and (B? int1) (N? int2)) (sA (B-gone int1))] |
| [(and (N? int1) (B? int2)) (sA (B-gone int2))] |
| [(and (A? int1) (N? int2)) (sB (plus (A-way int1) (make-N)))] |
| [(and (N? int1) (A? int2)) (sB (plus (make-N) (A-way int2)))] |
| ; missing case for plus-one |
| [(N? int) (make-Z)] |
The resulting code preserves the nice features of plus for Nats that made it efficient.
Having a representation for negative numbers allows us to
think about implementing subtraction.
We will implement subtraction in terms of negation, and
negation in terms of another helper function, flip,
which maps the representation
of \(i\) to the representation of \(-(i+1)\).
This can be done just by flipping Z to N,
N to Z, A to B,
and B to A.
Can you see why?
| (define (subt int1 int2) (plus int1 (negate int2))) |
| (define (negate int) (plus-one (flip int))) |
| (define (flip int) |
| (cond |
| [(N? int) (make-Z)] |
| [(Z? int) (make-N)] |
| [(A? int) (make-B (flip (A-way int)))] |
| [(B? int) (make-A (flip (B-gone int)))])) |
This also makes it clear that \(S(i)\) grows like the logarithm to the base 2 of the absolute value of \(i\).
To create a more readable version of Int, as before, we erase parentheses, replace make-A by \(0\) and make-B by \(1\), and read right-to-left. But we treat make-Z and make-N differently. We replace make-Z by the left-infinite sequence of zeroes, which we’ll write \(\ldots 0\). Similarly, we replace make-N by the left-infinite sequence of ones, which we’ll write \(\ldots 1\). This makes every integer into a left-infinite sequence of 0’s and 1’s.
We saw that \(-5\) was represented by (make-B (make-B (make-A (make-N)))). Its "readable" representation is \(\ldots 1011\).
4 = ...0100 |
3 = ...011 |
2 = ...010 |
1 = ...01 |
0 = ...0 |
-1 = ...11 |
-2 = ...10 |
-3 = ...101 |
-4 = ...100 |
-5 = ...1011 |
The representation of integers in modern computers (called two’s complement notation) consists of these bit sequences truncated to the rightmost 32 or 64 bits. For example, the representation of \(-5\) would be 11111111111111111111111111111011. Interpreted as a natural number instead, this 32-bit pattern represents 4294967291.
In creating the code for plus operating on Ints, we reused all the code for plus operating on Nats, and added some new cases. In hardware, this corresponds to being able to share components that implement functionality for both natural numbers (often called unsigned integers) and integers. The short code for negation and subtraction corresponds to a small amount of additional hardware to support those features.
Extended Exercise 35: Racket lists, instead of Racket structures, can be used to implement implement computations using a binary representation. We can represent Z by empty, (make-A x) by (cons 'o y), and (make-B x) by (cons 'i y), where y is the representation of x. Let’s call this representation an slist (short for "symbol list"). Note that the symbols used are formed with lower-case Roman letters.
Write the functions nat-to-slist and slist-to-nat, which are the translations of toNat and fromNat above. Here "nat" refers to the built-in natural numbers (using integers) in Racket. As an example, (slist-to-nat '(o i i)) should evaluate to 6. These functions are useful for your own testing. You should not use them (or built-in integers in any way) in the body of the two functions described below.
Next, write add, which consumes two slists and produces an slist, and is the translation of the version of add above that works on the binary definition of Nat. Your code should have the same efficiency. Writing short helper functions with well-chosen names will improve the readability of your code and aid in debugging.
Finally, write multiply, which consumes two slists and produces an slist representing their product. This requires pure structural recursion on only one parameter, not two as for add. It will use add as a helper function.
All your implementations should use structural recursion on lists. Make sure you try a few tests on the representations of very large numbers to confirm that your code is efficient. \(\blacksquare\)
Extended Exercise 36: Continuing on from the previous exercise, we can use slists to represent integers. We can represent Z by '(z), N by '(n), A x by (cons 'o y), and B x by (cons 'i y), where y is the representation of x. This is a recursive definition of slist suitable for representing all integers, and leads to a notion of structural recursion on slists which you should use for your solutions.
Write the functions int-to-slist and slist-to-int, which are the translations of fromInt and toInt, which in turn are the generalizations of fromNat and toNat from above. Here "int" refers to the usual representation of integers in Racket. As an example, (slist-to-int '(i i o n)) should evaluate to -5. As in the previous exercise, these functions are for testing purposes and not to be used in the bodies of the functions described below.
Next, write add, which consumes two slists and produces an slist, and is the translation of the version of plus above that works on the binary definition of Ints. Finally, write neg and minus (subtraction). As in the previous exercise, your functions must use structural recursion, and must be efficient. \(\blacksquare\)
Extended Exercise 37: The Fibonacci numbers are defined by \(f_0 = 0\), \(f_1 = 1\), \(f_n = f_{n-1} + f_{n-2}\) for \(n > 1\). They also have a closed-form solution: \(f_n = (\phi^n - (1-\phi)^n)/\sqrt{5}\), where \(\phi = (1+\sqrt{5})/2\). This formula is not effective for computing large Fibonacci numbers if implemented directly, because the use of square roots involves inexact numbers, and leads to errors. However, the final answer is a natural number, and all intermediate results are in a quadratic field as defined in exercise 9 in the Structures chapter. Using functions you wrote for that exercise together with some additional code, you can compute Fibonacci numbers exactly and efficiently using the closed-form solution.
Your task is to write a function fib that consumes a natural number \(n\) and produces the natural number \(f_n\) by evaluating the closed-form formula.
There is one operation in the closed-form solution that you did not handle in the earlier exercise, namely computing \(x^k\) for a quadratic field element \(x\) and a exponent \(k\) which is a natural number. It is simple to write this function using structural recursion on the unary definition of a natural number, but the resulting code is not efficient enough.
You can write an efficient exponentiation function using the binary definition of a natural number and structural recursion on the exponent. The goal is to make the number of recursive applications of the exponentiation function logarithmic in the exponent. Here is a template derived from toNat which you can use. Do not alter the recursive applications (which would violate structural recursion), or duplicate either of them (which would risk destroying the efficiency by doing repeated computation).
| (define (power x k) |
| (cond |
| [(zero? k) ...] |
| [(even? k) ... (power x (quotient k 2)) ...] |
| [(odd? k) ... (power x (quotient k 2)) ...])) |
You should be able to compute the following expression in a few seconds at most:
(if (> (fib 1000000) 0) true false)
If you are interested in doing more precise time comparisons, consider using a trick such as used in the expression above to avoid paying for displaying large results, and use the time form. Timings done inside DrRacket are usually suspect, and at the very least require turning off debugging in the "Show Details" portion of the language choice dialog. For the most accurate timing results, you have to run Racket from the command line in a terminal application, using the executable in the bin subdirectory of the Racket distribution. \(\blacksquare\)