We begin by considering jobs that execute with
perfect efficiency.
This is an admittedly unrealistic assumption,
but one that is useful in understanding and
quantifying the importance of the service demand
characteristic of a job (i.e., its work).
This is done by comparing a spectrum of allocation
algorithms that adaptively reallocate processing
power to jobs according to their remaining work,
.
The basis for comparison is
equipartition (i.e., 
).
Since jobs execute with perfect efficiency we
use 
in order to determine
processor allocations and examine a range of
values.
The results shown in Figure 2 have been
obtained by simulating a system
with P = 100 processors,
using a mean work requirement of 
,
and the coefficient of variation of work being
.
The graph plots the mean response time
as a function of the scheduling policy
( value)
and shows results for
loads (mean processor utilizations)
of 30%, 50%, 70%, and 90%.
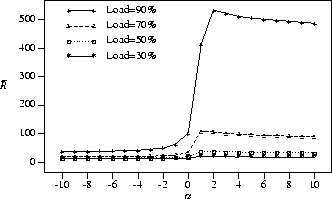
Figure 2: Mean response time vs. scheduling algorithm ( ); 
, perfectly efficient jobs
We first note,
as expected,
that the mean response times,
, obtained
with positive values of are very large
when compared with values of less than or
equal to zero.
This is because positive values of will
assign a larger portion of processors to larger
jobs (i.e., jobs with larger ).
The larger the value, the larger the
portion of processors assigned to the largest job.
With large enough ,
jobs are essentially executed in a Most Remaining Work First
(MRWF) fashion.
We include positive values in this
experiment mainly to point out that MRWF is not
pessimal.
We see that in this experiment, with a load of 90%,
is maximized
(there is a peak in the curve)
when 
.
This is because
the mean response time of
a MRWF first policy
can be increased by introducing processor
sharing among the largest jobs,
thus increasing the mean response time.
We also note that the difference in mean response time
across different scheduling policies
( values)
decreases as the load decreases.
This is because as the load gets lighter the
degree of multiprogramming decreases.
Under extremely low loads there will only be one job in
the system at any point in time,
in which case all of the allocation policies
behave in the same fashion
(i.e., the job is allocated all P processors).
In Figure 3 we more closely examine the range
.
This graph has been produced by running
experiments using a load of 90%
and increasing the coefficient of
variation of work.
We consider
.
In each case,
as increases in the negative direction
the mean response time decreases.
This is not surprising since
(as mentioned previously) all jobs execute with
perfect efficiency and a Least Remaining Work
First (LRWF) policy is optimal under these
conditions
[32, 3].
As well, as the coefficient of variation increases
so does the difference between and
, demonstrating the
increased benefits of knowing and appropriately
using the job characteristic .
We also point out that the shape of the
curves becomes sharper with increases in 
.
This is because with a small variation in ,
higher values of are required in order
to approximate a LRWF policy, while with larger
variations in smaller values of
can be used to approximate LRWF.
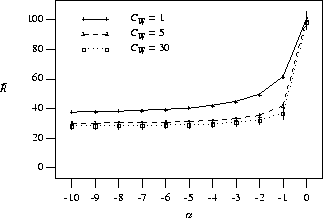
Figure 3: Mean response time vs. scheduling algorithm ( ); load=90%, perfectly efficient jobs
In Table 1 we provide a rough quantification
of the performance gains that can be achieved by
knowing and utilizing when jobs are
perfectly efficient and the load is 90%.
This table contains one column for the mean response times
and 90% confidence intervals for the two policies
and ,
as well as one column showing the percentage improvement
that is obtained by using
instead of .
It shows that for an improvement
of roughly 64% can be expected and that the
improvements likely increase with
(note the larger confidence intervals
for larger ).
This rough quantification is of interest because
it provides an approximate bound on the
reduction in mean response time
that can be obtained by using
(or 
).
This is because
workloads with less efficient jobs will
receive less benefit from allocating all processors
to one job at a time
(assuming a non-decreasing execution rate
function),
thus
reducing the difference between an equipartition
and an optimal policy.
As well,
previous analytic comparisons between LRWF and
equipartition policies
[3]
show that the
reduction in mean response time
obtained when all jobs
arrive simultaneously can be as large as 50%
and that the difference
can grow with the number of jobs
(i.e., it is not competitive)
when new arrivals are considered.
Since this previous result
assumes that
arrival times and job sizes are designed to
demonstrate maximum differences between the two
policies,
our comparison is important because it
provides more reasonable bounds
on the performance improvements that
might be expected.
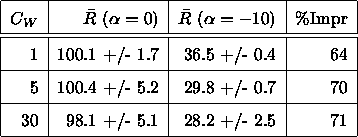
Table 1: Comparing mean response times for and for different ; load = 90%
These same experiments have also been conducted
under the assumption
that the work, , is not known
a priori (see [12] for details).
By keeping track of each job's accumulated execution
time and using that as an estimate of a job's
remaining work,
influenced by studies performed by Leland and Ott
on uniprocessor systems
[17]
(a portion of this study was
recently confirmed for modern workloads
by Harchol-Balter and Downey
[14]),
the response time is significantly reduced when
compared with equipartition,
although the reductions are not as large as when
is known.
We now explore the consequences of using only
information about a job's remaining work, ,
if jobs do not execute with perfect efficiency.
In this experiment we again choose
with a mean of and
.
Now instead of having all jobs execute with
perfect efficiency,
each job executes work at the
rate defined by the execution rate function
and the parameter
( 
).
In the following experiments we
generate values uniformly
between 
and 
and consider different workloads with different
and values.
The graph on the left side of
Figure 4 shows that for workloads
with relatively low average efficiency
( 
),
using only
to make scheduling decisions leads to
increased mean response times
(versus
equipartitioning processors, ).
This is because these policies
( 
)
are allocating
larger portions of the processors to small jobs
even though they may not be capable of utilizing
them effectively,
and are therefore essentially wasting
processing power.
However, the graph on the right side of
Figure 4 shows that for workloads
with high average efficiency
( 
),
using only
to make scheduling decisions can
decrease mean response times
(versus using no job characteristics and
equipartitioning processors, ).
This is because, under this workload,
the average efficiency of jobs is high enough that the
benefits of allocating
large portions of the processors to these jobs
(reduced response time)
outweigh the costs (under-utilized processors).
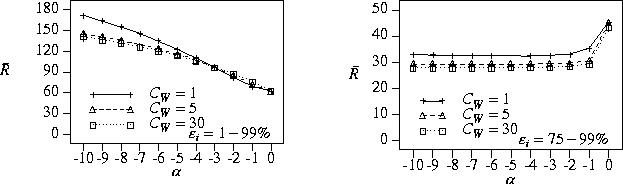
Figure 4: Mean response time vs. scheduling algorithm ( ); load=90%, jobs are not perfectly efficient