Peter van Beek
Cheriton School of Computer Science
University of Waterloo
Research: Optimization in machine learning.
Several important tasks in machine learning can be formulated as combinatorial optimization problems. For example, learning the structure of a Bayesian network from data can be formulated as a combinatorial optimization problem, where a score is defined that measures how well a candidate structure is supported by the observed data and the task is to find the structure with the lowest score. As a second example, learning a decision tree from labeled data can be formulated as a combinatorial optimization problem, where the goal is to find the decision tree that best fits the data subject to regularization constraints. Both of these problems are NP-Hard. Our approach is to apply constraint programming and other advanced search techniques.
Project: Exact Bayesian network structure learning
Citation
(PDF) Peter van Beek and Hella-Franziska Hoffmann. Machine learning of Bayesian networks using constraint programming. Proceedings of CP 2015, Cork, Ireland, August, 2015.
Abstract
Bayesian networks are a widely used graphical model with diverse applications in knowledge discovery, classification, prediction, and control. Learning a Bayesian network from discrete data can be cast as a combinatorial optimization problem and there has been much previous work on applying optimization techniques including proposals based on ILP, A* search, depth-first branch-and-bound (BnB) search, and breadth-first BnB search. In this paper, we present a constraint-based depth-first BnB approach for solving the Bayesian network learning problem. We propose an improved constraint model that includes powerful dominance constraints, symmetry-breaking constraints, cost-based pruning rules, and an acyclicity constraint for effectively pruning the search for a minimum cost solution to the model. We experimentally evaluated our approach on a representative suite of benchmark data. Our empirical results compare favorably to the best previous approaches, both in terms of number of instances solved within specified resource bounds and in terms of solution time.
Software and data
Code and data sets for the results described in the paper: README.txt, CPBayes.zip, Scores.zip
Table 1. For each benchmark set of discrete data, time (seconds) to determine minimal cost BN using various systems (see text) and the BDeu and BIC scoring methods, where n is the number of random variables in the data set, N is the number of instances in the data set, and d is the total number of possible parents for the random variables. Resource limits of 24 hours of CPU time and 16 GB of memory were imposed: OM = out of memory; OT = out of time. A blank entry indicates that the preprocessing step of obtaining the local scores for each random variable could not be completed within the resource limits.

Project: Local search for Bayesian network structure learning
Citation
(PDF) Colin Lee and Peter van Beek. Metaheuristics for Score-and-Search Bayesian Network Structure Learning. Proceedings of the 30th Canadian Conference on Artificial Intelligence, Edmonton, Alberta, May, 2017.
Abstract
Structure optimization is one of the two key components of score-and-search based Bayesian network learning. Extending previous work on ordering-based search (OBS), we present new local search methods for structure optimization which scale to upwards of a thousand variables. We analyze different aspects of local search with respect to OBS that guided us in the construction of our methods. Our improvements include an efficient traversal method for a larger neighbourhood and the usage of more complex metaheuristics (iterated local search and memetic algorithm). We compared our methods against others using test instances generated from real data, and they consistently outperformed the state of the art by a significant margin.
Software and data
Code and data sets for the results described in the paper: https://github.com/kkourin/mobs
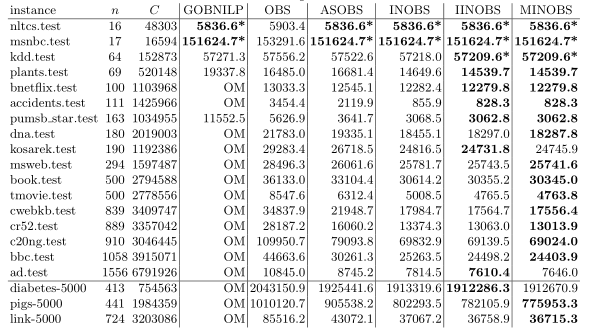
Table 1: Median score of best networks found, for various benchmarks, where n is the number of variables and C is the total number of candidate parent sets. The column labelled INOBS represents the scores of INOBS with random restarts. OM indicates the solver runs out of memory before any solution is output. Bold indicates the score was the best found amongst all tested methods. An asterisk indicates that the score is known to be optimal
Project: Anytime algorithms for Bayesian network structure learning
Citation
(PDF) Colin Lee and Peter van Beek. An Experimental Analysis of Anytime Algorithms for Bayesian Network Structure Learning. Proceedings of Machine Learning Research, Volume 73: Advanced Methodologies for Bayesian Networks (AMBN-2017), Kyoto, Japan, September, 2017 (slides).
Abstract
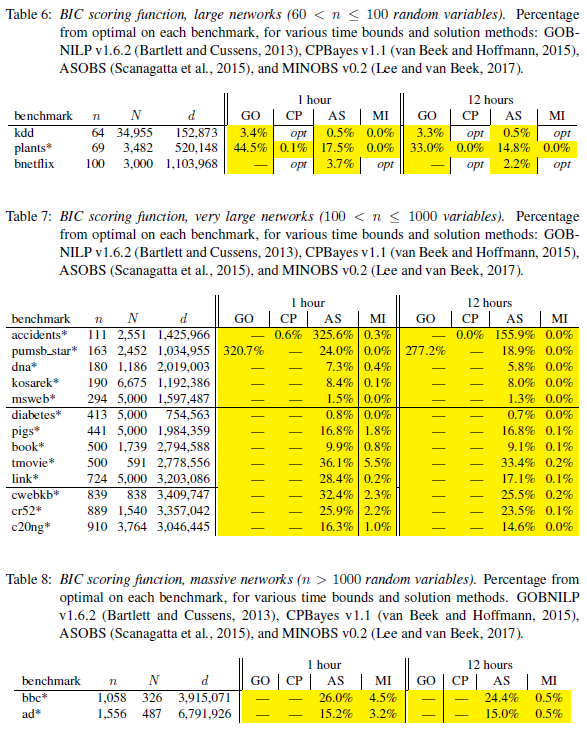
Bayesian networks are a widely used graphical model with diverse applications in knowledge discovery, classification, and decision making. Learning a Bayesian network from discrete data can be cast as a combinatorial optimization problem and thus solved using optimization techniques---the well-known score-and-search approach. An important consideration when applying a score-and-search method for Bayesian network structure learning (BNSL) is its anytime behavior; i.e., how does the quality of the solution found improve as a function of the amount of time given to the algorithm. Previous studies of the anytime behavior of methods for BNSL are limited by the scale of the instances used in the evaluation and evaluate only algorithms that do not scale to larger instances. In this paper, we perform an extensive evaluation of the anytime behavior of the current state-of-the-art algorithms for BNSL. Our benchmark instances range from small (instances with fewer than 20 random variables) to massive (instances with more than 1,500 random variables). We find that a local search algorithm based on memetic search dominates the performance of other state-of-the-art algorithms when considering anytime behavior.
Project: Bayesian network structure learning with side constraints
Citation
(PDF) Andrew C. Li and Peter van Beek. Bayesian Network Structure Learning with Side Constraints. Proceedings of the 9th International Conference on Probabilistic Graphical Models (PGM-2018), Prague, September, 2018 (poster).
Abstract
Hybrid methods for Bayesian network structure learning that incorporate both observed data and expert knowledge have proven to be important in many fields. Previous studies have presented both exact and approximate hybrid methods for structure learning. In this paper, we propose an approximate method based on local search that is capable of efficiently handling a variety of prior knowledge constraints, including an important class of non-decomposable \emph{ancestral} constraints that assert indirect causation between random variables. In our experiments, our proposed approximate method is able to significantly outperform an existing state-of-the-art approximate method in finding feasible solutions when hard constraints are imposed. Our approach is able to find near-optimal networks while scaling up to almost fifty random variables. In contrast, previous exact methods are unable to handle more than twenty random variables. Furthermore, we show that when prior knowledge is integrated, we are often able to produce a network much closer to the ground truth network, particularly when the amount of data is limited.
Table 1: Performance results for ancestral constraints only (first number in each pair) and with various constraints (second number in each pair). N is number of observations, % is the fixed percentage used to sample constraints, % feasible is the percentage of cases where the solution satisfied all constraints imposed, % sat is the percentage of satisfied constraints out of those constraints imposed, t is the running time required by the program. Highlighted cells indicate that not all constraints were able to be satisfied.
Project: Finding All Bayesian Network Structures within a Factor of Optimal
Citation
(PDF) Zhenyu A. Liao, Charupriya Sharma, James Cussens, and Peter van Beek. Finding All Bayesian Network Structures within a Factor of Optimal. Proceedings of 33rd AAAI Conference on Artificial Intelligence (AAAI-2019), Honolulu, January, 2019.
Abstract
A Bayesian network is a widely used probabilistic graphical model with applications in knowledge discovery and prediction. Learning a Bayesian network (BN) from data can be cast as an optimization problem using the well-known score-and-search approach. However, selecting a single model (i.e., the best scoring BN) can be misleading or may not achieve the best possible accuracy. An alternative to committing to a single model is to perform some form of Bayesian or frequentist model averaging, where the space of possible BNs is sampled or enumerated in some fashion. Unfortunately, existing approaches for model averaging either severely restrict the structure of the Bayesian network or have only been shown to scale to networks with fewer than 30 random variables. In this paper, we propose a novel approach to model averaging inspired by performance guarantees in approximation algorithms. Our approach has two primary advantages. First, our approach only considers credible models in that they are optimal or near-optimal in score. Second, our approach is more efficient and scales to significantly larger Bayesian networks than existing approaches.
Software
Code for the results described in the paper: https://github.com/alisterl/eBNSL