Net neutrality and Throughput Interference
The discussion about network neutrality spans almost two decades in Internet policy debate and literature. Yet, from a technical perspective, this discussion has been criticized as being largely oversimplified. In particular, the question which specific packet schedulers and/or service models conform to network neutrality has received little attention in the legal literature. Only FIFO scheduling has been discussed widely and it is often claimed that FIFO scheduling is necessary to attain network neutrality.
The current network neutrality rules in the USA do not require specific schedulers but instead establish three principles: 1) no blocking, 2) no throttling, 3) no paid prioritization. Further clarification seems necessary to apply these principles. The literature about detecting network neutrality violations typically uses a broader definition. In recent work, for example, network neutrality violations are detected by comparing each flow’s loss rate to a baseline loss rate, e.g., of some traffic aggregate. The network is neutral, if the difference between each flow and the baseline is sufficiently small. The same principle can be used to derive a metric for quantitatively assessing specific packet schedulers or service models.
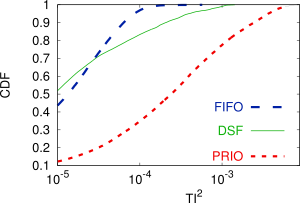
We propose a new metric to assess schedulers and service models without the need for a baseline: The throughput interference index TI² quantifies the degree by which a scheduler changes the throughput of multiple flows. Essentially, the TI² definition applies Jain's fairness index to relative throughput rates. If there are n flows, the TI² ranges from 0 to n−1/n with values closer to 0 indicating lower scheduler interference with throughput rates. In contrast, higher relative throughput differences result in a larger TI². This definition is backwards compatible with previous definitions. Firstly, FIFO indeed has a low TI² as formally shown in the extended version of our ITC 2016 paper. Secondly, this definition incorporates the no blocking and no throttling rules because it ensures that relative service rates correspond to relative arrival rates. Thirdly, this definition incorporates the loss-based metric from recent work, because the ratio λ(out)/λ(in) corresponds to 1-loss for each flow.
Formal definition of the throughput interference index (TI²)
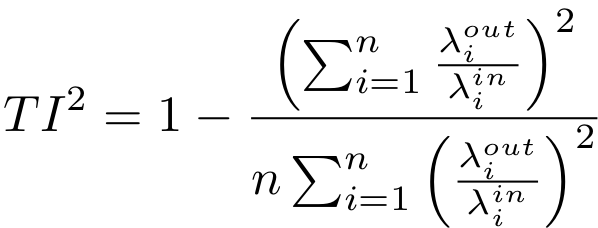where λ(in,i) and λ(out,i) are the input and output rates for a flow i.