RootFinding.mw
Root-Finding Methods
Define a function and its true root
| > |
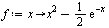 |
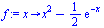 |
(1) |
Use Maple's fsolve to compute the root to 20 digit accuracy.
| > |
 |
 |
(2) |
| > |
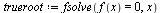 |
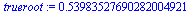 |
(3) |
Use 14 digit arithmetic for testing the methods, and set the tolerance for the stopping criteron.
| > |
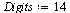 |
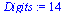 |
(4) |
| > |
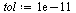 |
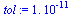 |
(5) |
Set the fail-safe maximum number of iterations.
| > |
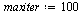 |
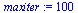 |
(6) |
Bisection method
| > |
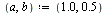 |
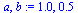 |
(7) |
| > |
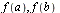 |
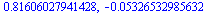 |
(8) |
| > |
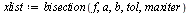 |
| > |
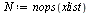 |
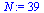 |
(10) |
Note: When testing the order of convergence for each of the methods, we choose to run the loop (see below) from  to
to 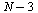 and therefore the last ratio tested compares the error in
and therefore the last ratio tested compares the error in ![xlist[`+`(N, `-`(2))]](images/RootFinding_49.gif) with the error in
with the error in ![xlist[`+`(N, `-`(3))]](images/RootFinding_50.gif) .
.
This is because as the iterates near convergence, one would need to compute with a higher setting of 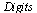 in order to get a true reading of the ratios. (This point is particularly relevant for the methods which converge at a faster rate.)
in order to get a true reading of the ratios. (This point is particularly relevant for the methods which converge at a faster rate.)
Test if the order of convergence is 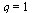 .
.
| > |
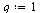 |
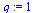 |
(11) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_55.gif) |
While we don't see a definite limit being reached, the ratios are not tending towards 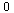 nor towards
nor towards 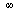 .
.
The bisection method has linear convergence (order 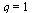 ).
).
More precisely, the stopping criterion used in the bisection method above is based on the length of the current interval ![[xleft, xright]](images/RootFinding_95.gif) . Since we start with an initial interval
. Since we start with an initial interval ![[a, b]](images/RootFinding_96.gif) which has length
which has length 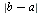 and at each iteration the new interval has length exactly half the preceding interval, it is clear that the ratio of successive interval lengths is exactly
and at each iteration the new interval has length exactly half the preceding interval, it is clear that the ratio of successive interval lengths is exactly 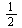 . This proves that the bisection method has linear convergence.
. This proves that the bisection method has linear convergence.
For example, let us test if the order of convergence is 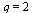 .
.
| > |
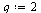 |
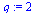 |
(13) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_102.gif) |
This time, the ratios are increasing towards 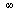 and therefore the hypothesized order
and therefore the hypothesized order 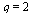 is too large.
is too large.
Fixed point iteration
| > |
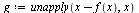 |
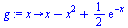 |
(15) |
| > |
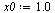 |
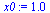 |
(16) |
| > |
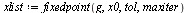 |
| > |
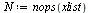 |
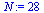 |
(18) |
Test if the order of convergence is 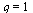 .
.
| > |
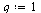 |
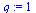 |
(19) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_166.gif) |
These ratios are approaching a nonzero finite constant.
Fixed point iteration has linear convergence (order 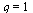 ), in general.
), in general.
Newton's method
| > |
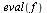 |
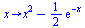 |
(21) |
| > |
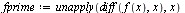 |
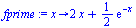 |
(22) |
| > |
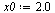 |
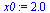 |
(23) |
| > |
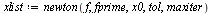 |
![[1.0, 2.0, 1.0332709786444, .63686054270010, .54511924037554, .53985256974508, .53983527708914, .53983527690281, .53983527690282]](images/RootFinding_209.gif)
![[1.0, 2.0, 1.0332709786444, .63686054270010, .54511924037554, .53985256974508, .53983527708914, .53983527690281, .53983527690282]](images/RootFinding_210.gif) |
(24) |
| > |
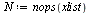 |
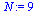 |
(25) |
Test if the order of convergence is 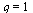 .
.
| > |
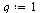 |
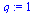 |
(26) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_216.gif) |
The ratios are decreasing towards 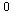 and therefore the hypothesized order
and therefore the hypothesized order 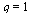 is too small.
is too small.
Test if the order of convergence is 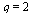 .
.
| > |
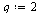 |
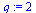 |
(28) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_228.gif) |
These ratios appear to be approaching a nonzero finite constant.
Newton's method has quadratic convergence (order 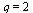 ).
).
Secant method
| > |
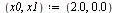 |
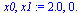 |
(30) |
| > |
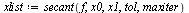 |
![[2.0, 0., .22561484995794, .74269471761917, .49760551690234, .53494633480234, .53996743772003, .53983487323262, .53983527686958, .53983527690282, .53983527690282]](images/RootFinding_250.gif)
![[2.0, 0., .22561484995794, .74269471761917, .49760551690234, .53494633480234, .53996743772003, .53983487323262, .53983527686958, .53983527690282, .53983527690282]](images/RootFinding_251.gif) |
(31) |
| > |
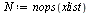 |
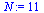 |
(32) |
Test if the order of convergence is 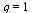 .
.
| > |
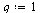 |
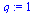 |
(33) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_257.gif) |
The ratios are decreasing towards 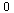 and therefore the hypothesized order
and therefore the hypothesized order 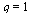 is too small.
is too small.
Test if the order of convergence is 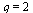 .
.
| > |
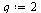 |
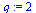 |
(35) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_271.gif) |
This time, the ratios are increasing towards 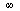 and therefore the hypothesized order
and therefore the hypothesized order 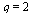 is too large.
is too large.
We conclude that the secant method has an order of convergence 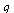 such that
such that 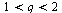 .
.
An analysis of the secant method proves that the order of convergence is the golden ratio:
| > |
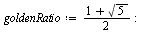 |
Test if the order of convergence is 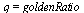 .
.
| > |
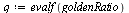 |
 |
(37) |
| > |
![for i to `+`(N, `-`(3)) do 'i' = i, ratio = `/`(`*`(abs(`+`(xlist[`+`(i, 1)], `-`(trueroot)))), `*`(`^`(abs(`+`(xlist[i], `-`(trueroot))), q))) end do](images/RootFinding_288.gif) |
These ratios appear to be approaching a nonzero finite constant.
The secant method has order of convergence 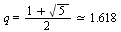 .
.
On the Efficiency of Root-Finding Methods
For measuring computational efficiency, the important measure is the number of function evaluations required to compute the root to the desired accuracy tolerance. This can be seen by noting that in every method, apart from function evaluations there are only a small number of simple arithmetic operations to be performed in each iteration.
Moreover, in practical applications the cost of evaluating the function may be relatively expensive.
For the root-finding problem considered above, we have the following comparisons.
Bisection method
| > |
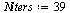 |
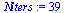 |
(39) |
| > |
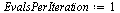 |
 |
(40) |
| > |
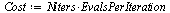 |
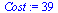 |
(41) |
Fixed point iteration
| > |
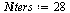 |
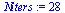 |
(42) |
| > |
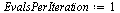 |
 |
(43) |
| > |
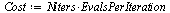 |
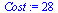 |
(44) |
Newton's method
| > |
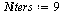 |
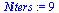 |
(45) |
| > |
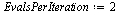 |
 |
(46) |
| > |
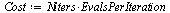 |
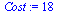 |
(47) |
Secant method
| > |
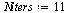 |
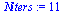 |
(48) |
| > |
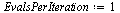 |
 |
(49) |
| > |
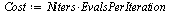 |
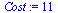 |
(50) |
Conclusion
Although Newton's method converges a little faster than the secant method, we see that the 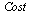 when measured by the number of function evaluations required to compute the root is significantly lower for the secant method.
when measured by the number of function evaluations required to compute the root is significantly lower for the secant method.
Among the methods discussed above, the secant method is the preferred choice. In fact, good software for root-finding generally combines the concept of the bisection method with the secant method. More specifically, a bracketing of the root is maintained throughout the computation (as in the bisection method) to avoid allowing the secant method to diverge away from the bracketing, while accepting secant iterations as long as they are converging to a root.