2-Point Rule
We develop Gaussian quadrature rules for the integral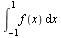 
on the standard interval ![[-1, 1]](images/GaussQuadrature_2.gif)
. For a general interval of integration ![[a, b]](images/GaussQuadrature_3.gif)
one can perform a simple transformation of variables.
For the 2-point rule, we must choose evaluation points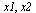 
and corresponding weights 
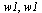such that the quadrature rule
| > |
 |
 |
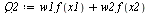(1) |
will be exact for integrating polynomials of as high a degree as possible.
Noting that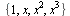 
forms a basis for all polynomials of degree 3, we set up four (nonlinear) equations in the four unknowns 
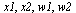as follows.
| > |
 |
 |
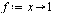(2) |
| > |
 |
 |
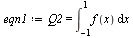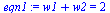(3) |
| > |
 |
 |
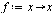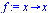(4) |
| > |
 |
 |
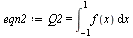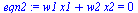(5) |
| > |
 |
 |
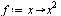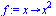(6) |
| > |
 |
 |
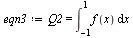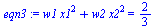(7) |
| > |
 |
 |
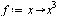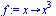(8) |
| > |
 |
 |
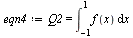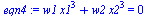(9) |
| > |
 |
 |
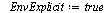(10) |
| > |
 |
 |
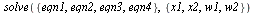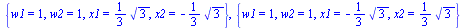(11) |
The solution we are interested in is the one with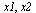 
in order from left to right.
Therefore the 2-point Gaussian quadrature rule for a general function 
is as follows.
| > |
 |
 |
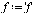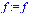(12) |
| > |
 |
 |
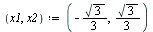(13) |
| > |
 |
 |
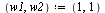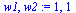(14) |
| > |
 |
 |
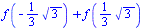(15) |
![nops([soln])](images/GaussQuadrature_75.gif){kind=small}
![soln[1]](images/GaussQuadrature_77.gif){kind=small}
![soln[2]](images/GaussQuadrature_79.gif){kind=small}
![soln[3]](images/GaussQuadrature_81.gif){kind=small}
![soln[4]](images/GaussQuadrature_83.gif){kind=small}
![soln[5]](images/GaussQuadrature_85.gif){kind=small}
![soln[6]](images/GaussQuadrature_87.gif){kind=small}
in order from left to right, namely ![soln[4]](images/GaussQuadrature_90.gif){kind=small}
is as follows. 
