RKMethods.mw
Runge-Kutta Methods
An IVP in Standard Form
The standard form for an IVP is the system of 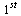 -order ODEs, with initial conditions:
-order ODEs, with initial conditions:
| > |
 |
| > |
 |
 |
![Y(t[0]) = Y0](images/RKMethods_5.gif) |
(1) |
where 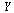 is a vector of functions and
is a vector of functions and 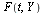 is a vector function of the scalar
is a vector function of the scalar 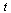 and the vector
and the vector 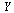 .
.
A 4th-order IVP
Let us use the following problem to test our numerical methods.
| > |
 |
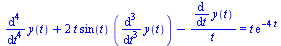 |
(2) |
with initial conditions
| > |
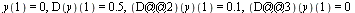 |
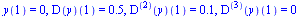 |
(3) |
The above inital value problem can be converted to a first-order system as follows. Introduce a new set of dependent variables:
| > |
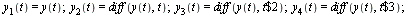 |
In terms of the new functions  the original
the original 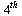 -order ODE becomes the following first-order system.
-order ODE becomes the following first-order system.
| > |

 |
with initial conditions
| > |
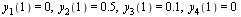 |
 = 0, y[2](1) = .5, y[3](1) = .1, y[4](1) = 0](images/RKMethods_28.gif) |
(6) |
This now takes the form of a standard first-order system:
| > |
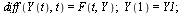 |
 |
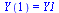 |
(7) |
where 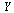 is a vector of dimension 4 and
is a vector of dimension 4 and  is a vector function of dimension 4 taking as arguments
is a vector function of dimension 4 taking as arguments 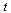 and the vector
and the vector 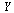 . Specifically,
. Specifically,
| > |
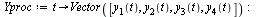 |
| > |
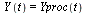 |
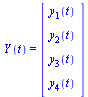 |
(8) |
| > |
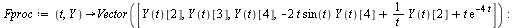 |
| > |
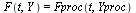 |
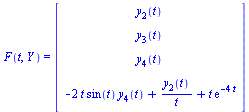 |
(9) |
The initial conditions are specified by the vector  :
:
| > |
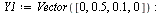 |
| > |
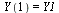 |
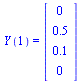 |
(10) |
Comparison Values
For comparison values when testing our numerical methods, apply the high-order method dverk78 to the original 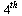 -order ODE.
-order ODE.
| > |
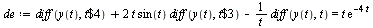 |
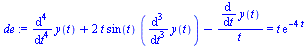 |
(11) |
| > |
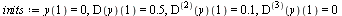 |
 |
(12) |
| > |
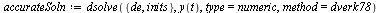 |
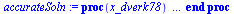 |
(13) |
For example:
| > |
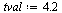 |
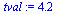 |
(14) |
| > |
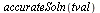 |
![[t = 4.20000000000000016, y(t) = 2.69988538740093586, diff(y(t), t) = 1.72666950368022687, diff(diff(y(t), t), t) = 2.79161521800559286, diff(diff(diff(y(t), t), t), t) = 15.5902337896826674]](images/RKMethods_56.gif)
![[t = 4.20000000000000016, y(t) = 2.69988538740093586, diff(y(t), t) = 1.72666950368022687, diff(diff(y(t), t), t) = 2.79161521800559286, diff(diff(diff(y(t), t), t), t) = 15.5902337896826674]](images/RKMethods_57.gif) |
(15) |
| > |
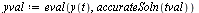 |
 |
(16) |
| > |
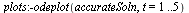 |
Runge-Kutta Method of Order 1
We have already seen a basic numerical time-stepping method of order 1, namely the Forward Euler Method:
| > |
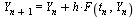 |
![Y[`+`(n, 1)] = `+`(Y[n], `*`(h, `*`(F(t[n], Y[n]))))](images/RKMethods_63.gif) |
(17) |
In the class of Runge-Kutta methods discussed below, the Forward Euler Method is a Runge-Kutta method of order 1.
Recall that the above formula is derived from the Taylor series expansion
| > |
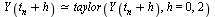 |
![`≈`(Y(`+`(t[n], h)), series(`+`(Y(t[n]), `*`((D(Y))(t[n]), `*`(h)))+O(`^`(h, 2)),h,2))](images/RKMethods_65.gif) |
(18) |
and by dropping the term 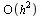 we arrive at the Forward Euler Method.
we arrive at the Forward Euler Method.
It follows that this method has local truncation error 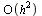 which leads to a global truncation error
which leads to a global truncation error 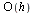 . Hence the method is order 1.
. Hence the method is order 1.
Test Order of Accuracy: RK1
The following procedure defines the method RK1 (otherwise known as the Forward Euler Method).
The IVP to be solved is
| > |
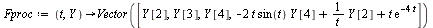 |
![proc (t, Y) options operator, arrow; Vector([Y[2], Y[3], Y[4], `+`(`-`(`*`(2, `*`(t, `*`(sin(t), `*`(Y[4]))))), `/`(`*`(Y[2]), `*`(t)), `*`(t, `*`(exp(`+`(`-`(`*`(4, `*`(t))))))))]) end proc](images/RKMethods_106.gif) |
(19) |
| > |
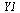 |
](images/RKMethods_108.gif) |
(20) |
Compute the solution a number of times specified by 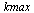 , dividing the stepsize
, dividing the stepsize 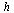 by 2 each time.
by 2 each time.
For each stepsize 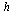 , compare the computed result at
, compare the computed result at  of the
of the 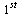 component of
component of 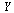 (which corresponds to the original
(which corresponds to the original 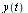 ), with the value
), with the value  .
.
| > |
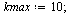 |
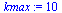 |
(21) |
| > |
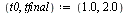 |
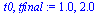 |
(22) |
| > |
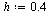 |
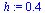 |
(23) |
| > |
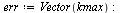 |
| > |
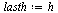 |
 |
(24) |
| > |
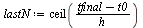 |
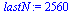 |
(25) |
| > |
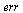 |
](images/RKMethods_136.gif) |
(26) |
Compute successive ratios
| > |
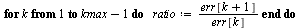 |
The ratio is approximately 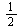 .
.
Conclusion: Since 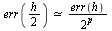 with
with 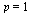 we conclude that RK1 is of order 1.
we conclude that RK1 is of order 1.
A Runge-Kutta Method of Order 2
We have previously developed a numerical time-stepping formula with a higher order, namely the Modified Euler Method which has order 2.
The Modified Euler Method can be stated in the following form, which is a common form for presenting Runge-Kutta formulas.
| > |
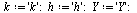 |
| > |
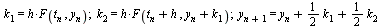 |
Recall that the above formula is based on the Taylor series expansion
| > |
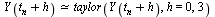 |
![`≈`(Y(`+`(t[n], h)), series(`+`(Y(t[n]), `*`((D(Y))(t[n]), `*`(h)), `*`(`*`(`/`(1, 2), `*`(((`@@`(D, 2))(Y))(t[n]))), `*`(`^`(h, 2))))+O(`^`(h, 3)),h,3))](images/RKMethods_156.gif) |
(29) |
by dropping the term 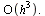
It follows that this method has local truncation error 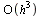 which leads to a global truncation error
which leads to a global truncation error 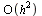 . Hence the method is order 2.
. Hence the method is order 2.
Test Order of Accuracy: RK2
The following procedure defines the method RK2 (otherwise known as the Modified Euler Method).
Compute the solution a number of times specified by 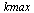 , dividing the stepsize
, dividing the stepsize  by 2 each time.
by 2 each time.
For each stepsize  , compare the computed result at
, compare the computed result at 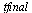 of the
of the 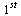 component of
component of 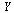 (which corresponds to the original
(which corresponds to the original  ), with the value
), with the value  .
.
| > |
 |
 |
(30) |
| > |
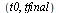 |
 |
(31) |
| > |
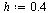 |
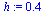 |
(32) |
| > |
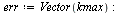 |
| > |
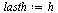 |
 |
(33) |
| > |
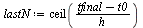 |
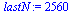 |
(34) |
| > |
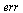 |
](images/RKMethods_224.gif) |
(35) |
Compute successive ratios
| > |
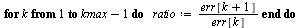 |
The ratio is approximately 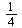 .
.
Conclusion: Since 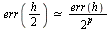 with
with  we conclude that RK2 is of order 2.
we conclude that RK2 is of order 2.
A Runge-Kutta Method of Order 3
For each order greater than 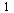 there is more than one possible Runge-Kutta method of the specified order.
there is more than one possible Runge-Kutta method of the specified order.
The following is a Runge-Kutta method of order 3.
| > |
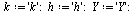 |
| > |
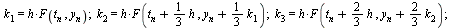
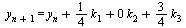 |
Note that for this particular choice of parameters, the value 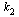 does not appear in the final formula although it is used in defining
does not appear in the final formula although it is used in defining 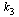 .
.
The parameters have been chosen to ensure that the local truncation error is  and therefore the global truncation error is
and therefore the global truncation error is 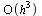 .
.
Test Order of Accuracy: RK3
The following procedure defines the method RK3.
Compute the solution a number of times specified by 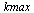 , dividing the stepsize
, dividing the stepsize 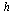 by 2 each time.
by 2 each time.
For each stepsize 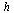 , compare the computed result at
, compare the computed result at 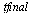 of the
of the 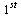 component of
component of 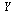 (which corresponds to the original
(which corresponds to the original 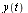 ), with the value
), with the value 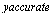 .
.
| > |
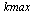 |
 |
(38) |
| > |
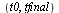 |
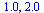 |
(39) |
| > |
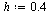 |
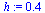 |
(40) |
| > |
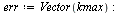 |
| > |
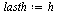 |
 |
(41) |
| > |
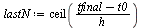 |
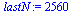 |
(42) |
| > |
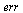 |
](images/RKMethods_315.gif) |
(43) |
Compute successive ratios
| > |
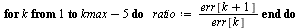 |
The ratio is approximately 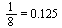 .
.
(Note that with a higher order method, the computed results stop improving because we reach the maximum accuracy for the given precision of the floating point arithmetic.)
Conclusion: Since  with
with 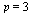 we conclude that RK3 is of order 3.
we conclude that RK3 is of order 3.
A Runge-Kutta Method of Order 4
The following is the most common Runge-Kutta method of order 4, as stated in the CS 370 Course Notes.
| > |
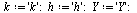 |
| > |
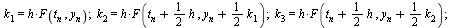
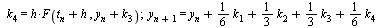 |
The parameters have been chosen to ensure that the local truncation error is 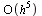 and therefore the global truncation error is
and therefore the global truncation error is 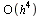 .
.
Test Order of Accuracy: RK4
The following procedure defines the method RK4.
Compute the solution a number of times specified by 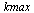 , dividing the stepsize
, dividing the stepsize 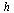 by 2 each time.
by 2 each time.
For each stepsize 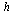 , compare the computed result at
, compare the computed result at 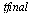 of the
of the 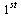 component of
component of 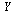 (which corresponds to the original
(which corresponds to the original 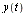 ), with the value
), with the value 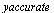 .
.
| > |
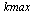 |
 |
(46) |
| > |
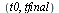 |
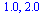 |
(47) |
Start with a larger value of  because the errors get very small quickly with this
because the errors get very small quickly with this 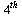 -order method.
-order method.
| > |
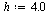 |
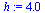 |
(48) |
| > |
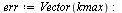 |
| > |
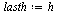 |
 |
(49) |
| > |
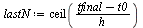 |
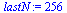 |
(50) |
| > |
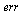 |
](images/RKMethods_403.gif) |
(51) |
Compute successive ratios
| > |
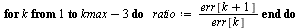 |
The ratio is converging to approximately 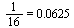 .
.
(Note that to get a better measure of the ratios, one would need to compute with higher-precision floating point.)
Conclusion: Since 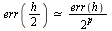 with
with 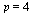 we conclude that RK4 is of order 4.
we conclude that RK4 is of order 4.
![]() -order ODEs, with initial conditions:
-order ODEs, with initial conditions: ![]() is a vector of functions and
is a vector of functions and ![]() is a vector function of the scalar
is a vector function of the scalar ![]() and the vector
and the vector ![]() .
. ![]() the original
the original ![]() -order ODE becomes the following first-order system.
-order ODE becomes the following first-order system. ![]() is a vector of dimension 4 and
is a vector of dimension 4 and ![]() is a vector function of dimension 4 taking as arguments
is a vector function of dimension 4 taking as arguments ![]() and the vector
and the vector ![]() . Specifically,
. Specifically, 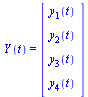
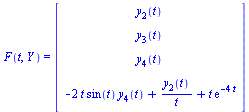
![]() :
: 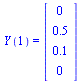
](images/RKMethods_136.gif)
](images/RKMethods_224.gif)
](images/RKMethods_315.gif)
](images/RKMethods_403.gif)