FFT_Timings.mw
Timing the FFT Algorithm
FFT Implementation via FFTeval
We developed procedure FFTeval which is used for the forward FFT and the inverse FFT, as follows.
| > |
 |
| > |
 |
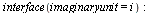where procedure FFTeval is as follows.
Timings using procedure FFTeval
| > |
 |
 |
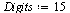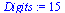(1) |
Form random vectors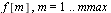 
where 
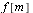is a vector of length 
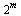containing floating point numbers in the following range.
| > |
 |
 |
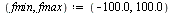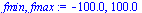(2) |
Choose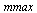 
as follows for this set of timings.
| > |
 |
 |
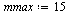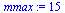(3) |
Collect timings for forwardFFT on successive vectors. Set the frequency of gc (garbage collection) higher than normal so as to minimize the effect of gc cost on the timings being collected.
| > |
 |
| > |
 |
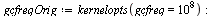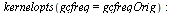Calculate the successive ratios of runtimes.
| > |
 |
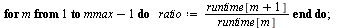We see that when the size of the vector is multiplied by 2, the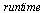 
increases by a factor only slightly larger than 2 (as 
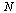gets large), illustrating that the cost function is nearly linear. As we have analyzed, the cost function is 
.
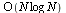DFT Implementation via GeneralPolyEval
For comparison purposes, let us define procedure GeneralPolyEval which uses general polynomial evaluation, not exploiting the special properties of the roots of unity. We will see that the runtime cost for this algorithm is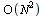 
.
Just as we defined procedures forwardFFT and inverseFFT by invoking procedure FFTeval, let us now define procedures forwardDFT and inverseDFT by invoking procedure GeneralPolyEval. This time they won't be "Fast" Fourier Transform algorithms because the cost will be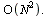 
Before calculating timings for these implementations, let us verify that procedures forwardDFT and inverseDFT compute the same results as procedures forwardFFT and inverseFFT, respectively.
| > |
 |
| > |
 |
 |
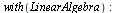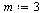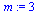(6) |
| > |
 |
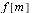](images/FFT_Timings_166.gif) |
(7) |
| > |
 |
 |
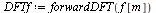(8) |
| > |
 |
 |
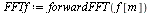(9) |
| > |
 |
 |
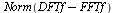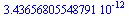(10) |
| > |
 |
 |
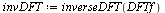(11) |
| > |
 |
 |
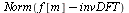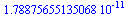(12) |
| > |
 |
 |
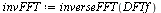(13) |
| > |
 |
 |
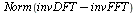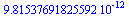(14) |
Timings using procedure GeneralPolyEval
Choose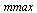 
not quite as large this time because the cost increases more quickly with this algorithm as 
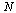gets large.
| > |
 |
 |
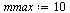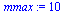(15) |
| > |
 |
| > |
 |
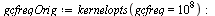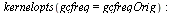Calculate the successive ratios of runtimes.
| > |
 |
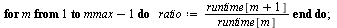This time, when the size of the vector is multiplied by 2 the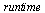 
increases by a factor of 4 (as 
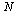gets large), consistent with an 
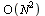algorithm.
Using DiscreteTransforms:-FourierTransform
An efficient implementation of FFT is provided in the DiscreteTransforms package in Maple, namely the functions FourierTransform and InverseFourierTransform. These implementations carry out all of the computations in hardware floating point arithmetic.
| > |
 |
We can choose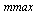 
larger in this case because the computations are much more efficient.
| > |
 |
 |
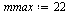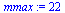(18) |
Collect timings for FourierTransform on successive vectors.
Calculate the successive ratios of runtimes, ignoring the first several values of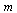 
because the runtimes are essentially zero.
| > |
 |
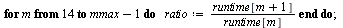We see that when the size of the vector is multiplied by 2, the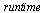 
increases by a factor close to 2 (as 
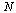gets large), illustrating that the cost function is nearly linear. As we know, the cost function is 
.
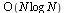Note that the timings for this implementation of the FFT are about 1000 times faster than our previous implementation. This is due to code that has been optimized to exploit hardware floating point arithmetic whereas our previous timings were computing in Maple's default "software floating point arithmetic".
Finally, let's verify that FourierTransform and InverseFourierTransform are computing correctly.
| > |
 |
 |
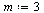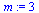(21) |
| > |
 |
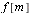](images/FFT_Timings_264.gif) |
(22) |
| > |
 |
 |
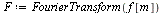(23) |
| > |
 |
 |
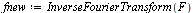(24) |
| > |
 |
 |
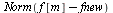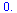(25) |
