In a uniprogrammed multiprocessor environment the execution time of a parallel program is mainly influenced the amount of basic work to be executed by the job. However, the execution time is also prolonged by a number of overheads incurred through the parallel execution of the job. These overheads include: the degree to which the work can be divided and balanced among multiple processors, the amount and type of communication among the cooperating processes, the amount and type of synchronization, as well as the costs incurred when creating and executing multiple processes on different processors. These different overheads can all be considered to be characteristics of the job being executed and can be modelled as inefficiencies in the ability of parallel programs to fully utilize the assigned processors. We use an execution rate function to model these inefficiencies.
In our job model two parameters are used to
characterize a job, 
.
--
is the amount of basic work executed.
This corresponds to the execution time
required to execute the program serially
(i.e., the service demand).
--
is a parameter to an execution rate function and
is used to characterize
the rate at
which the work, , is executed when
allocated a specified number of processors, 
.
This models the efficiency of the parallel job.
A number of models of parallel system and parallel program performance have been proposed and studied [10, 35, 7, 32]. We use the following execution rate function, used in a number of previous studies [5, 23, 30], which has been derived from an execution rate function (also called an execution signature) proposed by Dowdy [7]:
In this equation 
is the speedup obtained when
the job is executed on
processors and
is the parameter that is used to determine
the efficiency of the job.
If the number of processors allocated to a job,
,
is fixed for the duration of the job's execution
its execution time is therefore:
When working with the execution rate function, F,
we found it difficult to think in terms of
values for the execution rate.
For example, does 
imply
that the job attains good speedup?
The answer
depends on the number of processors
in the system, P.
Therefore,
we use a term called
effective efficiency, 
,
which expresses the speedup attained as a
percentage of the number of processors used if all
P processors would be allocated to the job.
Therefore,
means that if the
job was executed in isolation using all of the
processors its speedup would be 90% of P.
Alternately, E(P) = 0.90.
Note that if 
,
and that
a lower bound on is
, since the parameter ,
is bounded by zero.
Using
(rather than )
we gain an intuitive feeling for
possible values of,
and perhaps even representative distributions of,
.
Therefore,
we can think of and perform experiments
in terms of values
while the simulator internally uses the corresponding
values.
Figure 1 plots the execution
rate function using a number of
values
(corresponding values are
also shown),
assuming a system of 100 processors.
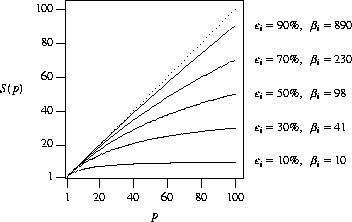
Figure 1: Execution rate function, speedup (S(p)) versus the number of
processors (p) for various
We recognize that this function does not accurately model the efficiency of all parallel applications because some applications may limit their parallelism (since they are unable to support P threads of execution efficiently) and because some applications will actually experience decreases in speedup when too many processors are allocated (due to increases in communication overhead). However, we chose not to use such models in this paper, because it could produce what might be considered an unfair bias against the equipartition policy. Since workloads can be easily generated on which the equipartition algorithm will perform poorly (because it will unknowingly allocate too many processors to jobs), developing algorithms that use job characteristics to improve mean response times would be trivial. Additionally, any algorithms developed using the model used here will only produce greater advantages when used with models of efficiency that consider jobs with limited parallelism and jobs that experience ``slowdown'' when too many processors are allocated. Note that more detailed and accurate models of efficiency, including a model that addresses both of these issues, are examined by Guha [12].