We now propose a new scheduling strategy that is
designed to take into account both the efficiency
of a job and its work.
This algorithm has evolved from our observations that
there are two main characteristics that contribute to
the response time of a parallel application,
the remaining work, 
, and the efficiency
with which that work can be executed, 
,
and that policies based on using either one of these
characteristics in isolation
are unable to significantly reduce mean response times
over the wide range of potential workloads
considered.
While it may be desirable to give less processing
power to jobs that execute large amounts of work,
in order to prevent them from delaying jobs that
execute smaller amounts of work,
it is also necessary to consider the efficiency with
which each job can utilize the allocated
processors.
We use a two-phased algorithm to determine the
number of processors, 
, to allocate to
each job 
.
Our strategy is to maintain a sorted list of jobs
in the system
(sorted by increasing ).
This ordered list is used to prevent short jobs
from being stuck behind large jobs.
Jobs are considered for activation
in this order and are assigned
processors, where
is determined
by considering the efficiency with which they execute.
During this first phase
jobs are assigned processors
until either all P processors have been assigned
or until all jobs have been activated.
If all jobs have been activated and
all P processors have not been assigned
a second phase is performed which assigns
the remaining processors to activated jobs.
A number of different assignment policies
are possible
for the first and second phases.
In this paper we focus our investigation
on policies for the first phase,
since we believe that the number of
unassigned processors left for the
second phase will be relatively small
(especially under workloads with relatively high
loads -- assuming the average efficiency is not
unreasonably low).
The policy used for the second phase
divides the remaining processors
equally among the active jobs (since this is a
safe approach).
An obvious strategy to use in the first phase is to
assign processors to each job according
to the knee of the
execution time - efficiency profile
( 
).
Unfortunately, this approach
has an important drawback:
is greater than P for jobs with
relatively low efficiency.
In fact, for P = 100 processors,
for all 
.
This may be
due to the execution rate function used.
However, no matter what execution rate function is
used there are likely to be some jobs whose
communication and synchronization overhead is
relatively small and therefore execute with high
efficiency.
In these cases their knee will be greater than the
number of processors in the system.
For such jobs the knee must be mapped into a
number of processors 
.
In future work we plan to consider alternative
execution rate functions and to investigate the importance
of appropriate mappings.
One way to avoid this problem is to simply
assign 
processors,
rather than .
However, this approach will allocate all P
processors to any job for which .
As expected, experiments showed
that this approach did not perform well for workloads
with high average efficiency, 
.
For example, using this policy to execute a
workload with 
,
= 50-99%, and a load of 90%
yields a mean response time that is 27% higher
than obtained using equipartition.
Therefore, we require a function
that more evenly maps the range, ,
to the domain, .
We start by considering an alternate, simple and obvious
mapping, 
.
The advantage of this policy is that only jobs with
high efficiency will be allocated a large number
of processors.
Also,
as the average efficiency of
the workload increases this algorithm
asymptotically behaves optimally
(i.e., if all jobs execute with perfect efficiency
they would be executed in a LRWF fashion).
We call the general form of our algorithm
(Work and Efficiency).
The form that uses
we call 
,
and the form that uses 
we call 
.
We have conducted a series of experiments to compare
with equipartition.
The results of these experiments are shown in
Figure 6.
These experiments were conducted
using arrival
rates that produced loads of
approximately 30% and 90% respectively.
An arrival rate was
determined using
and was then used for equipartition.
Each bar shown in these graphs
represents the mean response time of
,
normalized with respect to the mean response
time of equipartition
(represented by the dotted line, EQUI).
The workload for each experiment is specified
below the x-axis by displaying the
parameters 
and
the range 
.
As expected under low loads (30%),
the reductions in mean response time
obtained by using
instead of equipartition
are relatively small,
but statistically significant.
Again, this is because of the relatively low
degree of multiprogramming,
which reduces the
allocation alternatives.
Under this load equipartition is relatively robust
since the maximum observed improvement is about 15%.
As seen by the results obtained when a load of 90%
is used,
if the degree of multiprogramming is increased,
the size of the
reductions in mean response times increases.
Figure 6: Mean response time of for
different workloads, normalized with respect to EQUI
In the next series of experiments
(shown in Figure 7)
we consider
additional ranges of efficiency values
by also considering 
75-99%
and 99-99%.
These values are considered to emphasize that as
the average efficiency of the jobs increases,
the behaviour of our
policy approaches that of an optimal algorithm.
This can be seen by comparing the improvements
obtained in these graphs with those obtained in
Section 4.
These ranges demonstrate the substantial
reductions in mean response time that are possible
when the average efficiency of the jobs is high
and illustrate how the size of these reductions
grows with increases in average efficiency.
Additionally we study the affect that the
variation in job efficiencies, 
,
might have on our results.
This is done by fixing a mean efficiency and
examining different efficiency ranges.
We choose a fixed mean of 50%, since it offers the
greatest potential variation for our
distribution and
compare the ranges 1-99%, 30-70%, and 50-50%
(which produce of 0.57,
0.23, and 0.0 respectively).
The results in Figure 7 show that as
the variation in efficiencies decreases,
the mean response time obtained using
increases substantially when compared with
equipartition.
Figure 7: Mean response time of for
different workloads, normalized with respect to EQUI
Next we conducted a series of experiments
in order to determine if this increase is because
the general method, , is unable to handle
workloads with low variation in efficiency or because
the number of processors allocated during
the first phase could be improved.
We started by experimentally testing whether or
not a value of could be found that
improved the mean response time for the range
50-50% (under a load of 90%).
We found that by using the value 
,
we were able to produce mean response times that
were lower than those obtained using equipartition.
Further investigation found that for low
and high efficiency ranges (e.g., 1-20% and
80-99%) allocating processors
produced response times lower than for
equipartition.
Using these results we developed a simple
assignment policy that we hoped would uniformly
produce mean response
times equal to or lower than equipartition.
This new policy (or mapping) was derived
from our
observations that
performed reasonably well for
and for
and that
performed well for the workload with the efficiency
range 50-50%.
Therefore, we (naively)
chose a piecewise linear function
as the basis for a new
variation of our algorithm.
This variation is called 
and is described below.
The different forms of
the algorithm are shown in Figure 8.
Algorithmically this function is described
(for P = 100) as
follows:
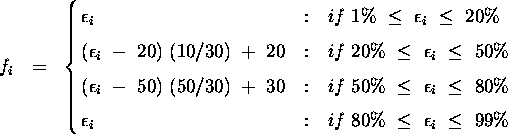
As shown in Figure 8,
when 
,
there is a large difference between the number of
processors allocated using
(i.e., using the knee) and using either
or
.
This seems to indicate that
under these job and workload models,
processor allocations in a dynamic
scheduling environment might be better made at a
point much lower than the knee.
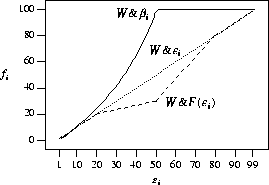
Figure 8: Different allocation policies considered for
The results of using this policy,
,
for a wide variety of workloads are shown in
Figure 9.
These experiments show that this policy does
produce mean response times that are at least as good as,
and are in many cases substantially better than,
those obtained with the
equipartition policy.
This policy therefore performs better across the
variety of workloads considered than the
, the
and the equipartition policies.
This suggests that
in a dynamic scheduling environment,
it may not be desirable
to allocate processors according to the knee of
the execution time - efficiency profile
(especially if a wide variety of workloads
are possible).
(We plan to further investigate
other factors, such as the load, the
execution rate function, and the distribution
used to generate the efficiency for each job.)
In the case when a load of 90% is used,
the largest improvement seen is approximately 70%.
A general trend that can be seen
by examining the ranges 1-50%, 50-99%, 75-99% and 99-99%
in this graph,
is that the size of the reductions
obtained by using
increases as the average efficiency increases.
It also seems that the size of the reduction
is correlated with the
coefficient of variation of work, ,
especially when the load and average
efficiency of the jobs is
relatively high.
We also point out again that
the reductions in mean response time are larger
for the workload whose range of efficiency is 1-99% than
for the range 30-70% even though the mean
efficiency has not changed.
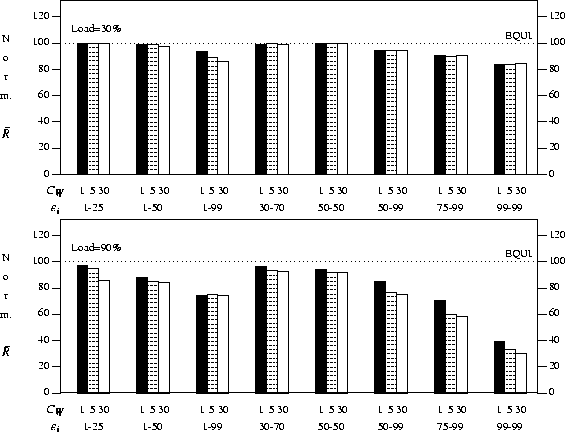
Figure 9: Mean response time of for
different workloads, normalized with respect to EQUI
Although the algorithm
can very likely be improved,
since it was chosen naively,
these experiments demonstrate that the
strategy is an attractive approach to using job
characteristics to make processor allocation
decisions in a dynamic scheduling environment.
If the number of processors to
assign during the first phase of the algorithm
is chosen properly,
this method can
produce mean response times that are
significantly lower than those obtained by using
equipartition across a wide variety of workloads.
As well, the
improvements are greater
than those that can be
obtained using only characteristics of work, ,
or efficiency, , in isolation.
We believe that these results demonstrate the
importance of using job characteristics correctly
as well as the need for allocation
policies that effectively use characteristics of
both work and efficiency.