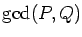
To determine the p-adic valuation of a Lucasnomial , i.e., of a generalized binomial coefficient with respect to a fundamental Lucas sequence U=U(P,Q), there is an adequate Kummer rule if p is a regular prime. No such rule exists if p is a special prime, i.e., if p divides . We provide a complete description of the p-adic valuation of Lucasnomials when p is special, with some numerical examples. Applications to the integrality of generalized Lucasnomial Fuss-Catalan numbers, Lucasnomial ballot and Lucasnomial Lobb numbers are also given.