Journal of Integer Sequences, Vol. 23 (2020), Article 20.6.7

Explicit Asymptotics for Signed Binomial Sums and Applications to the Carnevale-Voll Conjecture


Laurent Habsieger
Université de Lyon, CNRS UMR 5208
Université Claude Bernard Lyon 1
Institut Camille Jordan
43 boulevard du 11 novembre 1918
69622 Villeurbanne Cedex
France

Abstract:

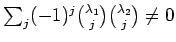
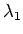
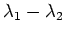
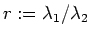
Carnevale and Voll conjectured that $\sum_j (-1)^j{\lambda_1\choose j}{\lambda_2\choose j}\neq0$ when $\lambda_1$ and $\lambda_2$ are two distinct integers. We check the conjecture when either $\lambda_2$ or $\lambda_1-\lambda_2$ is small. We investigate the asymptotic behaviour of the sum when the ratio $r:=\lambda_1/\lambda_2$ is fixed and $\lambda_2$ goes to infinity. We find an explicit range $r\ge 5.8362$ on which the conjecture is true. We show that the conjecture is almost surely true for any fixed r. For r close to 1, we give several explicit intervals on which the conjecture is also true.

Full version:  pdf,    dvi,    ps,    latex,     Maple code    

Received July 3 2019; revised versions received February 5 2020; February 9 2020; May 27 2020. Published in Journal of Integer Sequences, June 10 2020.

Return to Journal of Integer Sequences home page