 |
Journal of Integer Sequences, Vol. 14 (2011), Article 11.7.6 |
 |
Journal of Integer Sequences, Vol. 14 (2011), Article 11.7.6 |
Abstract:
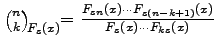 and
and
(Concerned with sequences
A000032
A000045
A010048
A034801.)
Received March 3 2011; revised version received July 13 2011. Published in Journal of Integer Sequences, September 5 2011.