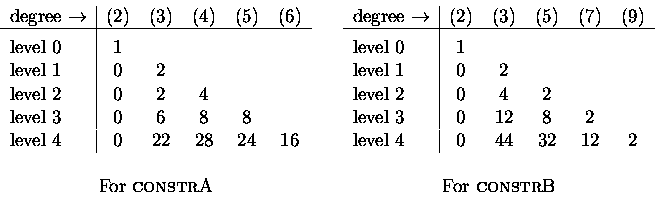
|
A parallelogram polyomino is a translation invariant array of unit squares bounded by two lattice paths that use the steps (0,1) and (1,0), and intersect only initially and finally. The semiperimeter of a polyomino is the length of either of these paths; the width of a polyomino is the number of its columns. We will consider parallelogram polyominoes consisting of black and white columns, called zebras. Barcucci, Del Lungo, Fezzi, and Pinzani [2] showed that R(n-1,n-1) counts the set of zebras with semiperimeter n. In the following we denote the cardinality of any set A by |A|. We denote the set of all zebras by Z, the semiperimeter of a zebra P by n(P), and the set {P in Z : n(P) = n} by Zn. It is convenient to take the trivial zebra to be the vertical unit segment denoted by |; hence, Z1 = {|}.
Before proceeding we recall from [5] the definition of a generating tree for a set of succession rules: A generating tree is a rooted, labeled tree in which the labels of the set of children of each node x are determined solely from the label of x. Thus any particular generating tree can be specified by a set of succession rules, i.e., a recursive definition, consisting of
The next two subsections record the generating trees of two constructions for zebras introduced by Barcucci et al.[2]. They focused on succession rules (or, rewriting rules) principally to study permutations with forbidden subsequences. Upon tabulating the frequency distributions for the out-degrees of the vertices at each level in the generating trees for the rules associated with the zebra constructions that follow, one can obtain arrays that contain the Schröder numbers, as in Table 2.
3.1 The construction CONSTRA
Theorem 7.3 of [2] gives the following inductive construction
for the set of all zebras. Beginning with Z1
= {|}, and assuming that Zn, ![]() ,
has been
constructed, one constructs all possible zebras of semiperimeter
n+1, each obtained from some zebra P in Zn, either
,
has been
constructed, one constructs all possible zebras of semiperimeter
n+1, each obtained from some zebra P in Zn, either
This construction essentially grows zebras by adding rows and
without changing the colors to the underlying parent zebra.
Its generating tree is illustrated in
Figure 1 and
the corresponding succession rules appear in Table 3.
Notice the appearances of the
Schröder numbers, both in the second column and as row sums,
in Table 2 that
gives the frequencies for the outdegrees of the vertices of the generating tree for this construction.
|
3.2 The construction CONSTRB
Theorem 5.2 of [2] gives a second construction for
the set of all zebras.
The construction begins with
![]() .
Assuming
that Zn,
.
Assuming
that Zn, ![]() ,
has been constructed, one constructs
Zn+1 to be the set of all
possible
zebras of semiperimeter n+1, each obtained from some parent
zebra P in Zn,
either
,
has been constructed, one constructs
Zn+1 to be the set of all
possible
zebras of semiperimeter n+1, each obtained from some parent
zebra P in Zn,
either
This construction essentially grows zebras by adding columns and without changing the color of the underlying parent zebra. The corresponding succession rules appear in Table 3. See also Table 2.