1 Introduction
\(\newcommand{\la}{\lambda} \newcommand{\Ga}{\Gamma} \newcommand{\ra}{\rightarrow} \newcommand{\Ra}{\Rightarrow} \newcommand{\La}{\Leftarrow} \newcommand{\tl}{\triangleleft} \newcommand{\ir}[3]{\displaystyle\frac{#2}{#3}~{\textstyle #1}}\)
"This might be your only chance / to prove it on your own"
(That’s How I Escaped My Certain Fate, Mission of Burma, 1980)
This flânerie is about the formalization of the idea of proof, and its application in computer science. It’s a rich and complex subject, and there is far more material than I can possibly cover without attempting to be encyclopedic. This is one possible approach to the subject; not the most widely-used approach, but one that I believe will be of particular interest to computer scientists.
In a nutshell, over the course of this stroll, if you do the recommended exercises, you will construct a very small proof assistant (which I call Proust) to help you construct and verify proofs of statements about programs. Furthermore, and this is the main novelty of this treatment (at least for my intended audience), the proofs themselves will be programs. You will think of them as programs, and you will use what you know of programming to construct them. In the process, you will learn the language and substance of formal logic. We’ll wrap up with a look at some larger systems that use the same principles and that are in use in research and industrial settings. By the end of this introductory chapter, I hope to convince you that this is a sensible approach, and that you should continue reading.
1.1 Required background
The programming to construct the proof assistant will be done in Racket, a functional programming language. There won’t be a lot of programming: a few hundred lines (not counting comments and tests). I will provide some starter code and you will extend it. It will help if you have programmed in Racket before, perhaps in a course based on How To Design Programs (HtDP), or by self-study, perhaps through my own flâneries Teach Yourself Racket (TYR, first three chapters), or Functional Introduction to Computer Science (FICS, in progress). Experience with another functional programming language (Haskell, OCaml, Clojure, Scala) would be a reasonable substitute. If you have none of these, you can pick up what you need as you go along, but you might want to look at TYR first, and experiment with DrRacket (the Racket IDE) a bit.
You could do the required programming in another functional language, or in any other programming language, but using DrRacket enables us to avoid a lot of unnecessary overhead. If you understand enough Racket to be able to translate the code I give you into another language, you probably know enough to just use DrRacket, and it will be less work in the end.
1.2 Prospective audience
You might consider spending time with this material if one or more of these hold:
You like programming and would like to get a better grasp on the ways in which you informally reason about programs;
You have interests in both mathematics and computer science (perhaps with more experience in one than the other) and would like to see how these two areas support each other;
You are intrigued by the features of static type systems such as found in Haskell, OCaml, Scala, and Rust, and would like to see the design principles involved;
You’ve heard of dependent types and would like a gentle introduction to them;
You’re interested in learning about proof assistants such as Coq and Agda in a low-magic way;
You’re a user of Coq, Agda, or some other proof assistant, and you’d like to understand more of what is happening behind the scenes;
You like puzzles, interesting diversions, complex historical personalities, and learning for its own sake.
This list is not exhaustive!
1.3 Design philosophy
This material was originally developed for an enriched version of a second-year undergraduate course required of all CS majors at the University of Waterloo. Most CS programs have a "discrete math" course, which teaches a bit of logic and Boolean algebra along with a grab-bag of other topics, such as combinatorics and probability. At Waterloo, we are fortunate to have CS located in a large Faculty of Mathematics. CS majors sit in classrooms beside majors in other mathematical disciplines, taking high-quality math courses.
Nonetheless, we have a CS-specific course titled Logic and Computation, because the standard mathematical treatment of formal logic usually leaves out the connections to computer science. Since nothing downstream directly depends on the material in this course, the style of an offering varies considerably with the instructor, from "math-like" to "engineering-like". Individual instructors of the course might be appreciated, but the course itself, in general, is not.
When I was granted the opportunity to teach the enriched version, I decided to not just throw a few more theorems into my standard version. Instead, I rethought the course from scratch, while remaining faithful to the high-level course description. I believed that having students build their own tools would improve their engagement with the material, as would having a proof language that was expressive enough to minimize tedium.
What I arrived at was a considerable departure from conventional practice in such courses, but it can illuminate and clarify those more mainstream approaches. This is not a voyage to a distant planet. It is a trip to a particularly beautiful (though underappreciated) part of the same country that others are exploring. At many points in the text, I take care to connect to what students might see if they looked at other courses or other reference works.
Although I developed this material for an enriched course, I don’t think it is harder than a conventional treatment; on the contrary, I think it is easier, more accessible, and more interesting. Some of the material can be challenging, particularly when it comes to showing that some things are impossible to prove or compute. I will warn you in advance of this, and give you a path by which you can skip such material on a first reading.
If you wish to seriously engage with this material, I think it is important that you do the programming and proof exercises. You won’t get the full benefit by just reading. Active learning is best, but there is no university credit system here to force you into it. I promise you that your voluntary choice will pay off. There aren’t any exercises in this introductory chapter, so you can finish reading it before deciding whether or not to commit.
1.4 The motivations for proof
Though my on-campus students exhibited considerable diversity, I could assume more about them than I can about you, the current reader. I’m going to assume that you know something about programming and are willing to learn more as needed, and that you’ve worked with some elementary data structures such as lists and trees. I’ll also assume that you have seen or will be comfortable seeing an elementary math proof (or at least a chain of reasoning) such as you might encounter in a late high school or early college/university course. I’ll be using set theory notation (e.g., membership, union) and the rudiments of relations (such as \(\le\), but defined on other sets), as well as some of the more commonly-used Greek letters, upper-case and lower-case.
The first course that our Faculty of Mathematics students take (Math 135/145) covers elementary number theory (the properties of integers). This is not because the topic is of critical importance in subsequent courses, but because it is an excellent vehicle for learning how mathematics is done. The course shows that proof is central to mathematics, and that proof consists of a structured, convincing argument that follows certain rules. It spends a lot of time explicitly talking about what constitutes a proof.
But even in a course this carefully designed, that has evolved and improved over decades, not all the rules are made explicit. There is an art in knowing what can be left out or implied in a proof. Facility in this comes only with experience. In your own math courses, you may have felt some frustration when you lost marks on a homework assignment because your argument was not valid, even though you thought it was.
Formalization of proof involves specifying the rules to the point where there can be no doubt about whether a proof is valid or not, because it is simple to detect a violation of the rules. Each part of a valid proof is a valid application of one of the completely-specified rules. Why isn’t this done in one’s first math course? Because a fully-formalized proof is often full of tedious detail. It’s something better suited for a machine to handle. As we’ll see, writing a program to check a formal proof is not difficult. Writing a program to create a formal proof, on the other hand, has been the subject of ongoing research for decades. The human mathematician is not yet obsolete.
While our first math course discusses proof extensively, there is no mention of proof in our first CS course, and this may mirror your own experience. Our first CS course does spend a lot of time discussing testing methods whose goal is to increase our confidence in the correctness of programs. (I hope yours did also!) But even those who follow careful testing practices will find that bugs lurk in their code. You may have experienced the frustration of submitting a program for a homework assignment that you thought was correct, but that failed some tests during the grading process. Or you may have felt some elation when you submitted a program that you knew was incorrect, yet it managed to pass all the tests used by the markers. The consequences of this mismatch are relatively minor in educational situations, but can be serious when software is used in critical applications.
This is where the notion of proving desired properties of programs comes in. The motivation for proof in computer science is similar to the motivation in mathematics. Proof arose in mathematics as an efficient alternative to exhaustive case analysis. It is not possible to verify a fact about the natural numbers (for example, that for all natural numbers \(n\), \(n^2+n\) is even) by checking it for every natural number. Even for finite situations, exhaustive checking may not be practical.
It’s not hard to see that this is also true for software. It is rare to be able to write an exhaustive test suite for a program, one that covers all cases completely. A finite (and hopefully short) proof in which one can have confidence might be a good alternative. The problem is that it seems much more difficult to prove a simple program correct than it does to prove a simple mathematical fact. It is hard enough to get programmers to write tests; it seems hopeless to ask them to write proofs. Consequently, the idea of proving correctness of programs is often dismissed as being impractical, and not relevant to the needs of programmers under pressure to quickly ship code.
To counter this belief, consider the fact that we really do want to write correct code, and we’d love to know that it is correct. We just don’t want to take forever doing so. As we write code, we think about what we are doing, and we believe what we are writing to be correct. We are reasoning about properties of the code we are writing, even if that reasoning is not as precise as a formal proof.
There is a spectrum of methods to try to increase our confidence in code. HtDP and FICS talk about the design recipe, a methodology for correct program development that can be used by the complete beginner. They also place emphasis on structural recursion, a design restriction that can facilitate code development. In FICS, I demonstrate that structural recursion facilitates formal proofs by induction, and is easier to reason about informally than non-structural recursion. You may have heard of other techniques or seen them in workplace settings: test-driven development, fuzz testing.
These techniques are optional, and again can be abandoned under pressure. But, in a sense, computers and programming languages are formal systems that don’t allow evasion. They have rigorous rules, and if you violate them, your program will stop running, or fail to run at all. We even accept additional rules that are not enforced in hardware, because they increase confidence in correctness. Many programming languages have a notion of type, a way of classifying values and restricting operations on them. The underlying hardware manipulates 32-bit or 64-bit quantities. The interpretation of those quantities is up to us, or to our software. We may choose, for example, to interpret those as integers. Consider the function that consumes two integers and produces the sum of their squares. We can write it this way in the functional programming language OCaml.
let ssq (x : int) (y : int) : int = x * x + y * y. |
This definition declares the parameters x and y to be integers, as well as the result. The code looks somewhat different in Racket, not only because the syntax is different (all operators appear before their arguments) but because there is no explicit mention of types.
(define (ssq x y) (+ (* x x) (* y y)))
Evaluation in a pure functional programming language can be explained by a substitution model similar to algebraic substitution as taught in high school. This model is discussed in HtDP and FICS, and taught in our first CS course. Using the right-pointing arrow => to represent one substitution step, we might trace the application of the ssq function to the values 3 and 4 as follows.
(ssq 3 4) => (+ (* 3 3) (* 4 4)) => (+ 9 (* 4 4)) => (+ 9 16) => 25
There are two kinds of substitution here. The first step is the substitution of the value of the parameters into the body expression of the function. Subsequent steps replace the application of a predefined or built-in function such as * or + to values with the result. For example, in the second step, (* 3 3) is replaced with 9. In a more complicated example, these two kinds of substitution might be interspersed with each other, and with other substitutions defined for other Racket language features.
This trace can be viewed as a proof of the statement "The Racket expression (ssq 3 4) evaluates to 25." In general, a proof of a statement about a program has to involve reasoning about evaluation. If the proof is to be formal, the evaluation model must also be formal.
The application of the ssq function to 3 and 4 succeeded because 3 and 4 are numbers to which the operations * or + can be applied. The two Boolean values in Racket are #t and #f (to which the more readable names true and false are bound). These Boolean values are not numbers. They are represented by the underlying machine architecture as specific 32-bit or 64-bit quantities, and the machine will permit those quantities to be multiplied. But a Racket program will not. Here is what happens in the evaluation model when we try to apply ssq to #t and 7.
(ssq #t 7) => (+ (* #t #t) (* 7 7))
The next step would be replacing (* #t #t) with its value. But multiplication cannot be carried out on Boolean values. When the program is run in DrRacket, the software halts program execution and produces an error message at the point where the multiplication is attempted.
OCaml will not let one get even this far. The OCaml compiler performs a static analysis (known as typechecking) that can detect this possibility, and will not compile or run a program that contains an application of ssq to an argument that does not typecheck as integer. Writing a OCaml program with the intention of having it successfully compile is a modest use of a formal system. This is not unique to OCaml, or to functional programming languages; mainstream languages that use static type analysis include Java and C++.
Racket views types as a characterization of values. The type "Boolean" has two values, #t and #f. Other values have different types. Racket’s policy of signalling error at run time when an operation is applied to a value of the wrong type is known as strong dynamic typing. (Weak typing would let one get away with this sometimes.)
OCaml extends this view of types from values to subexpressions in a program. Because 3 is an integer, the expression (3 + 3) can also be typed as integer, without actually evaluating it. To describe the type of a function, we can borrow mathematical notation. The type of a function that consumes a Boolean value and produces a string is \(\mathit{Bool}\ra\mathit{String}\). The OCaml compiler must be able to compute the type of every subexpression in a program before it will compile and run the program. This is known as strong static typing.
Typechecking can be viewed as a simple form of proof, and it is one that is used by many programmers on a regular basis. Type systems vary in their expressivity. It’s common to be able to say "this value is an integer", but not very common to be able to say "this value is an even integer". But the latter statement may be important to our notion of correctness of a particular program. We need a rich language in which to express such statements, and a practical notion of proof. As it turns out, types can play a significant role in this quest. To see how, let’s examine the nature of a proof more closely.
1.5 Informal proof in mathematics
You have probably seen mathematical proofs before, and they probably looked fairly formal to you, as will the example in this section. But I prefer to reserve the term "formal proof" for one where all the rules of proof construction and validity are clearly spelled out. So the following proof, and probably the ones you saw before, will be considered "informal" in our current context.
Although we will not focus on properties of integers in what follows, I would like to pull in some early materials from our Math 135 course, because they provide an accessible example of theorem statement and proof. The theorem concerns divisibility, which is defined in the Math 135 notes this way: "We write \(m \mid n\) when there exists an integer \(k\) so that \(n = km\)." As an example, we can say that 2 divides 6, or \(2 \mid 6\) in this notation, because \(6 = 3(2)\), so the required integer \(k\) is \(3\) in this case.
The definition of divisibility is a logical statement expressing a relationship between \(n\) and \(m\). If we are more precise about the language of a logical statement, we could call it a logical formula, but we’re not going to do that right away. The notation \(m \mid n\) is designed to make theorems like the following one (from the Math 135 notes) a little more readable.
Divisibility of Integer Combinations (DIC): Let \(a\), \(b\) and \(c\) be integers. If \(a \mid b\) and \(a\mid c\), then for any integers \(x\) and \(y\), \(a \mid (bx+cy)\).
Theorems like this may or may not be provable. Here is the proof of DIC, again quoted directly from the Math 135 notes:
"Assume that \(a\mid b\) and \(a\mid c\). Since \(a\mid b\), there exists an integer \(r\) such that \(b=ra\). Since \(a \mid c\), there exists an integer \(s\) such that \(c = sa\). Let \(x\) and \(y\) be any integers. Now \(bx + cy = (ra)x + (sa)y = a(rx + sy)\). Since \(rx + sy\) is an integer, it follows from the definition of divisibility that \(a \mid (bx + cy)\)."
By the end of this stroll, you will be able to formalize proofs like this in a way that a full-fledged proof assistant can accept. But for the time being, notice that there is some unfolding of definitions (such as \(a\mid b\)), some explicit equational reasoning, some explicit logical reasoning ("Since... it follows that.."), and some implicit mathematical reasoning (uses of the distributive, commutative, and associative laws to manipulate algebraic expressions).
I can use this proof to help motivate my proposed approach to formalizing it. Looking at the second sentence of the statement of the theorem, we see that it is a conditional statement. It is of the form "If A, then B", where A and B are also logical statements. The first sentence of the proof says "Assume A", and the rest of the proof works out the consequences of that assumption, ending by concluding B. This is a standard method for proving conditional statements: assume the premise A, and then use that assumption to derive the conclusion B.
Let’s visualize this. We don’t yet know what precise form our formalization will take, so I’ll draw this type of proof as a cloud.
The assumption of A might be used at several points in the proof. Let’s mark each use with an X.
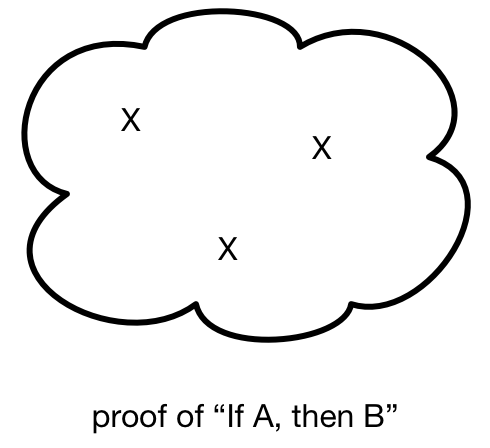
This is a proof of "If A, then B". It’s not a proof of A. We don’t know whether A can be proved, and this proof says nothing about that. It’s also not a proof of B (even though it concludes B somewhere inside) because of those unjustified assumptions of A. We don’t know whether B can be proved, and this proof says nothing about that, either.
But suppose someone gave us a proof of A.

We can use this to construct a proof of B. What we do is take the proof of "If A, then B", and replace every place where A is assumed with the complete proof of A. That might be repetitive, but the result has no assumptions, and it concludes B. We have created a complete, self-contained proof of B.
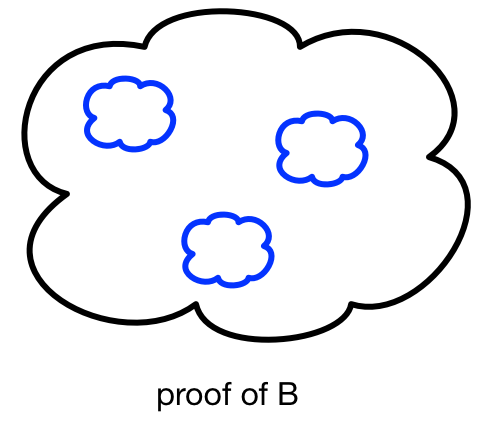
This construction should remind you of something you saw earlier in this chapter. The substitution looks like the one done when we apply a Racket function to argument values. We replace the parameter x with the value of the argument everywhere in the body expression.
(define (ssq x y) (+ (* x x) (* y y))) (ssq 3 4) => (+ (* 3 3) (* 4 4))
Continuing the analogy, the proof of "If A, then B" looks like the body of a function with parameter X. Applying this function to a proof of A produces a proof of B. To summarize, we can view a proof of "If A, then B" as a function that consumes a proof of A and produces a proof of B.
This is the central idea that we will use in our formalization of proof. We will create a small functional programming language in which to write proofs. Extending it to other logical constructs will incorporate other recognizable programming constructs in our proof language. The tool you write will not only check proofs written in this language, but help you to develop them interactively. I call the program Proust in reference to the French novelist Marcel Proust, but mostly because it is a small, quickly-developed proof assistant, and if you say "proof assistant" really quickly, it sounds like "Proust".
I hope this approach will allow you to leverage your experience with and love of programming to good effect in the study of logic. You may never be as enthusiastic about logic as you are about programming... but you might be.
1.6 Informal proof in computer science
To conclude this introductory chapter, I would like to show you a small example of an informal proof of properties of a Racket program. This will give you some sense of the capabilities we might eventually want to incorporate in Proust, and will serve as a warmup for the use of Racket as an implementation language in subsequent chapters.
The program involves manipulation of lists. Lists are a fundamental data structure in most functional programming languages, and they are generally constructed the same way (syntax will differ). There is an empty list value, denoted by '() in Racket, to which the more readable name empty is bound. Nonempty lists can be constructed using the cons constructor, which consumes an arbitrary Racket value v and a list value lst, and produces a list that has v as the first element and lst as the rest of the list. The list containing the numbers 1, 3, 2 in that order is (cons 1 (cons 3 (cons 2 '()))), which can be abbreviated by (list 1 3 2) or even '(1 3 2).
This results in a self-referential or recursive definition of list: a list is either empty, or is (cons v lst) for some value v and list lst. The two cases can be distinguished by the empty? predicate. A nonempty list can be deconstructed by applying the unsurprisingly-named functions first and rest.
This allows us to write code that processes lists in a form that mirrors this definition, termed structural recursion. For example, to compute the length of a list, we look at these two cases. If the list is empty, its length is zero. If the list is nonempty, it is of the form (cons v lst), in which case the length of the list is one plus the length of lst.
Using the functions described above, and a Racket cond (conditional) expression, which evaluates a series of "question" expressions and produces the first answer corresponding to a true value, we can translate this English description into Racket code.
(define (length lst) (cond [(empty? lst) 0] [else (add1 (length (rest lst)))]))
If you cannot make sense of this code, please go and spend some time with TYR, FICS, or HtDP in order to gain more confidence with Racket. You don’t need to understand the proof I am about to present in order to continue reading, but you will need to write some Racket code fairly soon.
We can prove some simple things about the length function with fairly simple reasoning. Consider the following statement:
"For all lists lst and values v, (length (cons v lst)) = (add1 (length lst))."
Here equality means "evaluates to the same thing". (Later we will have a more extensive discussion of the meaning of equality, and remembering this example will help.) This statement can be proved by a trace.
(length (cons v lst)) => (cond [(empty? (cons v lst)) 0] [else (add1 (length (rest (cons v lst))))]) => (cond [#f 0] [else (add1 (length (rest (cons v lst))))]) => (add1 (length (rest (cons v lst)))) => (add1 (length lst))
I haven’t been precise about the evaluation rules for cond expressions, but I hope this makes sense. It isn’t really a trace, because v and lst are left unspecified, so the evaluation rules, strictly speaking, cannot be applied. But if those symbolic values are replaced by actual values, that creates a legitimate trace.
This sort of reasoning, where a "for all" statement is proved by abstract manipulation of symbolic values, does not always suffice. To see an example where it falls short, let me define another list function, one which "glues" two lists together. The result of evaluating (append '(1 3 2) '(5 4)) should be '(1 3 2 5 4). We can code append using structural recursion on the first argument (the second argument does not need to be deconstructed).
(define (append lst1 lst2) (cond [(empty? lst1) lst2] [else (cons (first lst1) (append (rest lst1) lst2))]))
It should be the case that for all lists l1 and l2,
(length (append l1 l2)) = (+ (length l1) (length l2)).
This is an example of a simple property of our simple code,
standing in for more complex properties of more complicated code.
But trying to reason about this as we did for length alone above
does not seem to work.
We arrive at a more complicated version of what we are trying to prove.
We need a more sophisticated technique.
Let’s be slightly more precise about what we are proving: "For all lists l1, for all lists l2, (length (append l1 l2)) = (+ (length l1) (length l2))." This is a nested for-all statement. We will prove the outer for-all statement in the following way. To prove a property of all lists, we need to prove it for the empty list. If we can also prove that the property is preserved by cons, then it must be true for all lists. What does "preserved by cons" mean? It means that if the property holds for a list lst, then for all values v, the property holds for (cons v lst).
We have to accept this as valid reasoning, but I hope it makes intuitive sense. Let’s try to do this for the specific property we have in mind.
In the case of the empty list, the statement we are required to prove is "For all lists l2, (length (append empty l2)) = (+ (length empty) (length l2))". Symbolic manipulation suffices to prove this part. We can simplify the left-hand side of the equality using the code for append and the substitution model for evaluating Racket expressions; the left-hand side becomes (length l2). Similarly, we can simplify the right-hand side of the equality to (length l2), so the two sides of the equality are in fact equal. (If you’re not convinced, do the trace as we did above.)
Now suppose we have a list lst, and the property holds for it,
that is, for all lists l2,
(length (append lst l2)) = (+ (length lst) (length l2))."
We need to show that the property holds for any list (cons v lst),
that is, for all lists l2,
(length (append (cons v lst) l2)) = (+ (length (cons v lst)) (length l2)).
Again, we can simplify using the substitution model. The left-hand side of the equality we are proving becomes (add1 (length (append lst l2))), and by the fact that the property holds for lst, this is (add1 (+ (length lst) (length l2))). The right-hand side of the equality becomes (+ (add1 (length lst)) (length l2)), so clearly the two sides are equal. This concludes the proof.
The technique we used here is known as structural induction. It applies to other forms of data with recursive definitions. We will later see how to add it to Proust, and how some larger proof assistants deal with it. If you’d like more practice before that, try proving that for all lists lst, (append lst empty) = lst, in a manner similar to the proof above.
1.7 What next?
Three major chapters follow this one. The first (that is, the second chapter of the stroll) is the study of propositional logic, essentially what we can do with the logical constructs of implication, AND, OR, and negation. This includes being quite precise about definitions and notation. Using Racket, we will soon construct a simple version of our homemade proof assistant Proust, and then add more features to it gradually. The second section covers predicate logic, which adds the quantifiers "for all" and "there exists", equality, and domains of application such as the natural numbers. Again, we’ll modify and extend Proust to deal with these. In the final chapter, we will move from Proust to the much more complex and fully-featured proof assistants Agda and Coq, and see examples of their use in developing certified software.
If you’ve studied functional programming, you may have had to "unlearn" some ideas about computing in order to properly grasp the new concepts. Something similar may happen here. What you now have to grapple with is the process of taking concepts that may have been exercised informally, and making them precise. That earlier informal exposure may have blurred or overlapped ideas that now have to be separated. Be prepared with an open mind and a willingness to recognize and question assumptions.
The system we are developing differs in two key aspects from most other treatments: our logic will be constructive, or intuitionistic as opposed to classical, and it will be higher-order as opposed to first-order. You don’t have to understand these differences right now; I will explain them when the time is right. But these differences may also require some mental adjustment. Hopefully you will find enough rewards in the material to make it worthwhile.
"Beside, if you stay / I’d feel a certain guilt / Did I hold you back?"
(That’s How I Escaped My Certain Fate, Mission of Burma, 1980)