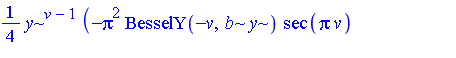Risch Algorithm for Elementary Functions
The Problem
Given a function ![]() , determine whether there exists a function
, determine whether there exists a function ![]() such that
such that

i.e. determine an indefinite integral, or antiderivative, of ![]() . We will write
. We will write
![]()
where we do not explicitly write the arbitrary constant of integration.
A detailed development of the Risch integration algorithm presented here can be found in the textbook [Geddes92]. Additional material on the Risch algorithm appears in [Bronstein90b], [Bronstein97].
In this presentation, examples will be shown using the Maple computer algebra system.
Example 1.1
| > | restart; |
| > | f := x*(x+1)*( (x^2*exp(2*x^2) - ln(x+1)^2)^2 +
2*x*exp(3*x^2)*( x - (2*x^3+2*x^2+x+1)*ln(x+1) )) / ((x+1)*ln(x+1)^2 - (x^3+x^2)*exp(2*x^2) )^2: |
| > | Int(f,x); |
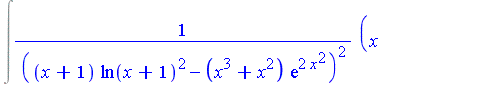
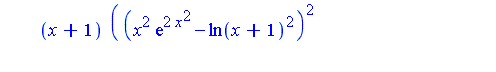
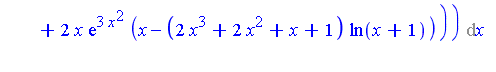
| > | value(%); |

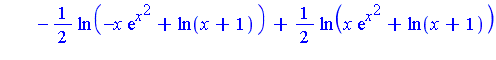
| > |
- Does there exist a function
 in a specified class of functions such that
in a specified class of functions such that  ?
? - If yes then determine
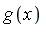 .
. - For
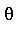 in
in 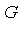 , if there exists
, if there exists 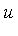 in
in 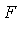 such that
such that 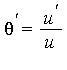 then we write
then we write 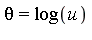 and
and 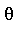 is called logarithmic over
is called logarithmic over  .
. - For
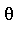 in
in 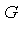 , if there exists
, if there exists 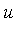 in
in 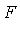 such that
such that 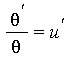 then we write
then we write 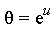 and
and 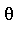 is called exponential over
is called exponential over 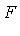 .
. - For
 in
in 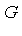 , if there exists a polynomial
, if there exists a polynomial  in
in 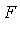 [
[ ] such that
] such that 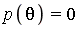 then
then 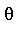 is called algebraic over
is called algebraic over 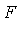 .
. 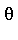 in
in 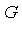 is transcendental over
is transcendental over 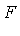 if
if  is not algebraic over
is not algebraic over 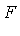 .
.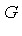 is called a transcendental elementary extension of
is called a transcendental elementary extension of 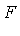 if
if  where each
where each 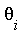 is transcendental and either logarithmic or exponential over the field
is transcendental and either logarithmic or exponential over the field  .
.- Similarly,
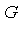 is an elementary extension of
is an elementary extension of  if each
if each 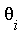 is logarithmic, exponential or algebraic over
is logarithmic, exponential or algebraic over 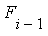 .
. - If
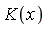 denotes a differential field of rational functions over a constant field
denotes a differential field of rational functions over a constant field 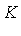 (a subfield of the complex numbers) and if
(a subfield of the complex numbers) and if 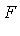 is an elementary extension of
is an elementary extension of 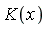 then
then 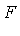 is called a field of elementary functions.
is called a field of elementary functions. - Similarly,
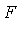 is called a field of transcendental elementary functions if
is called a field of transcendental elementary functions if 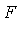 is a transcendental elementary extension of
is a transcendental elementary extension of 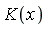 .
.
Defining the function field
The Risch integration algorithm is a decision procedure by which we mean that given an integrand ![]() , the algorithm will determine:
, the algorithm will determine:
If the answer to the existence question is no then the algorithm has constructed a proof of nonexistence.
Such a decision procedure is only possible in a context where we have clearly specified the class of functions (the function field) containing ![]() . For example, we will consider the field of elementary functions. In this function field, the Risch algorithm will determine that the integral
. For example, we will consider the field of elementary functions. In this function field, the Risch algorithm will determine that the integral 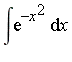 does not exist. However, if we allow the question to be expanded beyond the field of elementary functions then this integral can be expressed, as shown below by Maple.
does not exist. However, if we allow the question to be expanded beyond the field of elementary functions then this integral can be expressed, as shown below by Maple.
| > | Int(exp(-x^2), x) = int(exp(-x^2), x); |
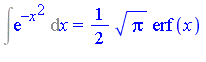
| > |
Definition of Elementary Functions
Let ![]() be a differential field (i.e. a function field on which derivation is defined) and let
be a differential field (i.e. a function field on which derivation is defined) and let ![]() be a differential extension field of
be a differential extension field of ![]() . Let the derivation operation be denoted by prime ( ' ) .
. Let the derivation operation be denoted by prime ( ' ) .
Notation for elementary functions
Note that the common notation for elementary functions does not make it clear that an elementary function can be described using only the three types of extensions defined above.
Examples in common notation
| > | Int(1/(1+x^2), x) = int(1/(1+x^2), x); |
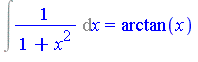
| > | Int(cos(x), x) = int(cos(x), x); |
![]()
| > | Int(1/sqrt(1-x^2), x) = int(1/sqrt(1-x^2), x); |
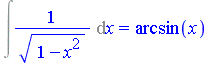
| > | Int(arccosh(x), x) = int(arccosh(x), x); |
![]()
| > |
In the examples above, each integrand and each integral result involves only elementary functions. To see that these functions conform to the definition of elementary functions of the preceding section, we must convert the functions to complex exp-log form.
The same examples in exp-log notation
| > | Int(1/(1+x^2), x) = convert(int(1/(1+x^2), x), 'expln'); |
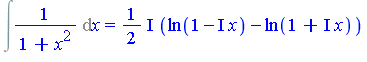
| > | Int(1/2*exp(I*x) + 1/2*exp(-I*x), x) = int(1/2*exp(I*x) + 1/2*exp(-I*x), x); |
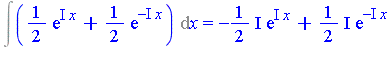
| > | Int(1/sqrt(1-x^2), x) = convert(int(1/sqrt(1-x^2), x), 'expln'); |

| > | Int(convert(arccosh(x),'expln'), x) = int(convert(arccosh(x),'expln'), x); |
![]()
![]()
| > |
We can now see a relationship between the input (the integrand) and the output (the integral result). Namely, the types of functions which can appear in the integral result are the same functions that appear in the integrand plus, in some cases, new log extensions. This fact is known as Liouville's Principle: the only new functions needed are constant multiplies of log extensions.
The common notation hides this relationship.
Liouville's Principle
Theorem 1
Given ![]() in an elementary function field
in an elementary function field ![]() ,
, ![]() , if it exists as an elementary function, can be expressed in the form
, if it exists as an elementary function, can be expressed in the form
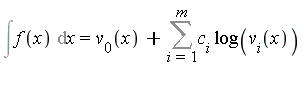
with ![]() in
in ![]() ,
, ![]() constants, and
constants, and ![]() in
in ![]() .
.
Note: The constants ![]() may involve new algebraic number extensions.
may involve new algebraic number extensions.
Integral of a rational function
Given a rational function ![]() , Liouville's Principle states that its integral can be expressed as a rational function plus (possibly) some constant multiples of
, Liouville's Principle states that its integral can be expressed as a rational function plus (possibly) some constant multiples of ![]() functions. (Note that Maple's notation for the natural logarithm function is
functions. (Note that Maple's notation for the natural logarithm function is ![]() rather than
rather than ![]() .)
.)
For the case of rational functions, the integral always exists as an elementary function.
Example 1.2
| > | restart; |
| > | Int(1/(x^2+2*x+1), x) = int(1/(x^2+2*x+1), x); |
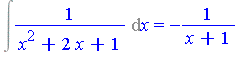
Remark: No ![]() terms required in the above example.
terms required in the above example.
| > | Int(1/(x^3+x), x) = int(1/(x^3+x), x); |
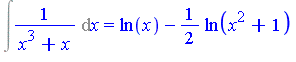
Remark: No algebraic number extensions required in the above example.
| > | Int(1/(x^2-2), x) = `int/risch`(1/(x^2-2), x); |
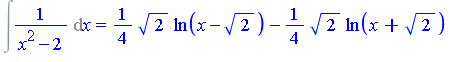
Remark: In the latter example, the constant field needed to be extended by the algebraic number ![]() .
.
| > |
Minimal algebraic extensions are desired for efficiency.
For example, from above noting that ![]() would lead to the following representation of the integral:
would lead to the following representation of the integral:
 .
.
Goal: Avoid introducing algebraic numbers except when necessary.
Hermite Reductions for the Rational Part
We want to reduce the problem as follows:

where ![]() and where
and where ![]() is monic and square-free.
is monic and square-free.
Hermite's method is a classical method to achieve this reduction. The reduction is accomplished using basic polynomial operations and without introducing any algebraic number extensions. The method is summarized here.
Step 1: Euclidean division with remainder yields
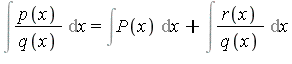
where ![]() or
or ![]() .
.
Step 2: Square-free factorization yields
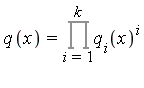
where ![]() for all
for all ![]() ,
,
and where ![]() for
for ![]() .
.
Step 3: Partial fraction expansion yields
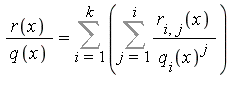
where ![]() .
.
We now have
 .
.
Step 4: Hermite reductions must be applied for each integrand where the denominator is a power ![]() >
> ![]() of a square-free factor.
of a square-free factor.
After this step, each integral that remains will have a square-free denominator.
Consider one integral 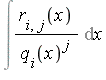 with
with ![]() >
> ![]() .
.
Apply the Extended Euclidean Algorithm to solve: ![]() .
.
This yields /q[i](x)^j, x) = Int(s(x)/q[i](x)^(j-1), x)+Int(t(x)*q[i](x)^`'`/q[i](x)^j, x)](images/IntSurvey_117.gif) .
.
Integration by parts yields
^`'`/q[i](x)^j, x) = -t(x)/((j-1)*q[i](x)^(j-1))+Int(t(x)^`'`/((j-1)*q[i](x)^(j-1)), x)](images/IntSurvey_118.gif)
^`'`/q[i](x)^j, x) = -t(x)/((j-1)*q[i](x)^(j-1))+Int(t(x)^`'`/((j-1)*q[i](x)^(j-1)), x)](images/IntSurvey_119.gif)
![]() .
.
Note the contribution to the rational part of the result.
Hermite reductions can be continued until only square-free denominators remain.
Example 1.3
| > | p := x^6+5*x^5+10*x^4+50*x^3+25*x^2+127*x-1: |
| > | q := x^4+10*x^2+25: |
The integral we wish to compute is
| > | Int(p/q, x); |
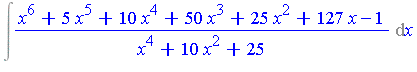
| > | r := rem(p, q, x, 'P'); |
![]()
| > | P; |
![]()
| > | int_P := int(P, x); |
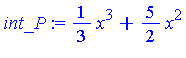
Euclidean division with remainder has yielded:
| > | Int(p/q, x) = int_P + Int(r/q, x); |
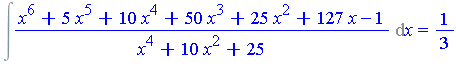
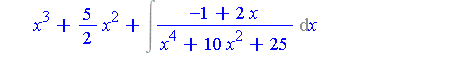
| > | q_sqrfree := convert(q, sqrfree, x); |
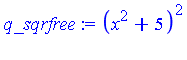
| > | q2 := x^2 + 5; |
![]()
In this case, the square-free factorization of the denominator is
![]() with
with ![]() and
and ![]() .
.
The problem has been reduced to
| > | Int(p/q, x) = int_P + Int(r/q2^2, x); |
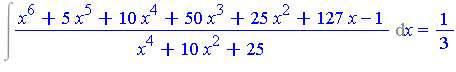

Apply Hermite reduction to the remaining integral which is of the form ![]() with
with ![]() .
.
The Extended Euclidean Algorithm is invoked as follows.
| > | gcdex(q2, diff(q2,x), r, x, 's', 't'); |
| > | s; |
![]()
| > | t; |
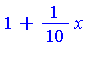
| > | j := 2: |
The Hermite reduction formula takes the form
| > | Int(r/q2^j, x) = -t/((j-1)*q2^(j-1)) + Int((s+diff(t,x)/(j-1))/q2^(j-1), x); |
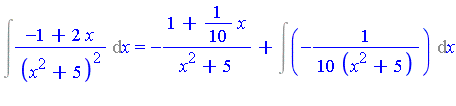
and therefore the original integral has been reduced to
| > | Int(p/q, x) = int_P + rhs(%); |


| > |
Rothstein-Trager Theorem for the Logarithmic Part
The problem is to express 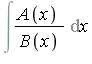 where
where ![]() and
and ![]() is square-free.
is square-free.
Classical approach: Factor B(x) over its splitting field, and then a partial fraction expansion determines the ![]() terms.
terms.
But such a factorization may be much more expensive than necessary.
Theorem 2 (Rothstein-Trager Theorem)
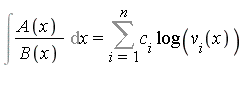
where ![]() are the distinct roots of
are the distinct roots of ![]()
and where ![]() are the polynomials
are the polynomials ![]() .
.
Moreover, this expresses the integral using the minimal algebraic extension field.
Remark: The roots of ![]() may introduce new algebraic numbers.
may introduce new algebraic numbers.
Example 1.4
From Example 1.3 the remaining integral is
| > | A := -1/10: B := x^2 + 5: |
| > | Int(A/B, x); |
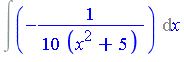
| > | R := resultant(A - z*diff(B,x), B, x); |

| > | (c1,c2) := solve(R=0, z); |
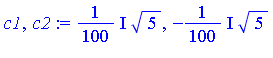
| > | v1 := gcd(A - c1*diff(B,x), B); |
![]()
| > | v2 := gcd(A - c2*diff(B,x), B); |
![]()
Therefore the integral can be expressed as follows.
| > | Int(A/B, x) = c1*log(v1) + c2*log(v2); |
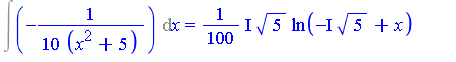

| > |
In this case, the result is identical to that obtained by the "classical approach" where the denominator is completely factored.
Example 1.5
One of the integrals from Example 1.2 is
| > | A := 1: B := x^3+x: |
| > | Int(A/B, x); |
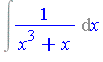
| > | R := resultant(A - z*diff(B,x), B, x); |
![]()
| > | solve(R=0, z); |
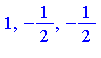
The distinct roots are
| > | (c1,c2) := (1,-1/2); |
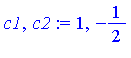
| > | v1 := gcd(A - c1*diff(B,x), B); |
![]()
| > | v2 := gcd(A - c2*diff(B,x), B); |
![]()
Therefore the integral can be expressed as follows.
| > | Int(A/B, x) = c1*log(v1) + c2*log(v2); |
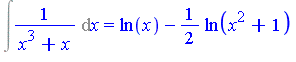
In contrast, the "classical" approach would require a complete factorization of the denominator
| > | factored_B := factor(B,I); |
![]()
| > | integrand := convert(A/factored_B, parfrac, x); |
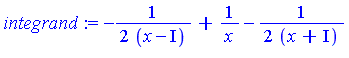
from which we see that the integral is
| > | Int(A/B, x) = map(`int/risch`, integrand, x); |
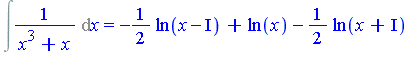
| > |
The Rothstein-Trager method avoids introducing the algebraic number extension ![]() in this example.
in this example.
Computational cost increases significantly with each new algebraic number extension, so it is important to use the minimal number of extensions required by the problem.
The case of transcendental elementary functions
Step 1: Determine a description ![]() of a function field containing the integrand
of a function field containing the integrand ![]() .
.
![]() is the constant field (we dynamically extend it to include any algebraic numbers which may arise).
is the constant field (we dynamically extend it to include any algebraic numbers which may arise).
We must ensure that each ![]() is a new transcendental extension. (This allows the manipulation of the integrand as a rational expression in the independent symbols
is a new transcendental extension. (This allows the manipulation of the integrand as a rational expression in the independent symbols ![]() .)
.)
Example 1.6
For the integral
| > | restart; |
| > | Int(1/ln(x), x); |

the integrand lies in the function field ![]() where
where ![]() is a logarithmic extension of the rational function field
is a logarithmic extension of the rational function field ![]() .
.
In this field the integrand is
| > | 1/theta; |
![]()
| > |
Example 1.7
For the integral
| > | Int((x^3+2*x)*cos(x^2)+x*sin(x^2), x); |
![]()
by converting the integrand to complex ![]() -
-![]() form, the problem can be expressed in the form
form, the problem can be expressed in the form
| > | Int((x^3+2*x)*(exp(I*x^2)+exp(-I*x^2))/2 - 1/2*I*x*(exp(I*x^2)-exp(-I*x^2)), x); |
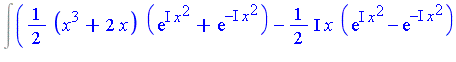

and we can view the integrand as an element of the function field ![]() where
where 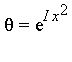 . (Note:
. (Note: ![]() .)
.)
In this field the integrand is
| > | 1/2*(x^3+2*x)*(theta + 1/theta) - 1/2*I*x*(theta - 1/theta); |
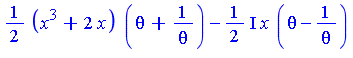
| > |
Example 1.8
For the integral presented in Example 1.1
| > | Int(x*(x+1)*( (x^2*exp(2*x^2) - ln(x+1)^2)^2 +
2*x*exp(3*x^2)*( x - (2*x^3+2*x^2+x+1)*ln(x+1) )) / ((x+1)*ln(x+1)^2 - (x^3+x^2)*exp(2*x^2) )^2, x); |

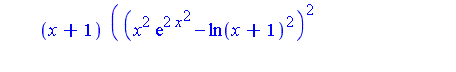
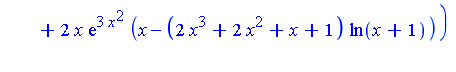

we can view the integrand as an element of the function field ![]() where
where 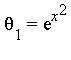 and
and ![]() .
.
Note that the two exponential terms ![]() and
and ![]() cannot be considered as independent extensions because there is an algebraic relationship between them. Rather, we choose to represent these terms in the form
cannot be considered as independent extensions because there is an algebraic relationship between them. Rather, we choose to represent these terms in the form 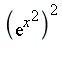 and
and 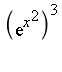 which involves a single transcendental extension
which involves a single transcendental extension  .
.
| > |
Step 2: Consider the integrand ![]() as a rational expression in the field
as a rational expression in the field ![]() :
:

where ![]() denotes the last extension and where
denotes the last extension and where ![]() . In other words,
. In other words, ![]() and
and ![]() are viewed as polynomials in the domain
are viewed as polynomials in the domain ![]() [
[![]() ] . Normalize
] . Normalize ![]() such that
such that ![]() and
and ![]() is monic.
is monic.
The algorithm proceeds in a manner similar to rational function integration; specifically, Hermite reductions followed by the application of a Rothstein-Trager Theorem. In particular, the algorithm will apply polynomial operations. We consider separately the cases where the last extension ![]() is a logarithmic extension or an exponential extension.
is a logarithmic extension or an exponential extension.
Integral of a logarithmic extension
Suppose that the last extension ![]() is a logarithmic extension, i.e.
is a logarithmic extension, i.e. 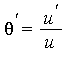 for some function
for some function ![]() in
in ![]() . Applying Euclidean division with remainder yields
. Applying Euclidean division with remainder yields 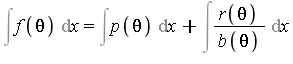 .
.
We now have two integrals to consider: (1) the integral of the polynomial part; and (2) the integral of the rational part. This time (unlike the case of rational function integration) the integral of the polynomial part is nontrivial; indeed, task (1) is the harder of the two parts. We first consider task (2).
Hermite Reductions for the Rational Part (log extension)
This case mimics the Hermite method for rational functions. Applying square-free factorization of the denominator yields 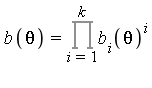 where this means "square-free as a polynomial in
where this means "square-free as a polynomial in ![]() ." For application in subsequent steps of the algorithm, we need to know that the following theorem holds.
." For application in subsequent steps of the algorithm, we need to know that the following theorem holds.
Theorem 3: If ![]() is a monic polynomial which is square-free as a polynomial in the symbol
is a monic polynomial which is square-free as a polynomial in the symbol ![]() and if
and if ![]() for some function
for some function ![]() then
then
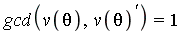
where the latter differentiation is with respect to ![]() .
.
Then applying partial fraction expansion, we get
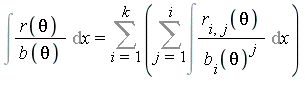 where
where ![]() .
.
For each integral with a denominator containing a power ![]() >
> ![]() , apply the Extended Euclidean Algorithm to solve
, apply the Extended Euclidean Algorithm to solve
+t(theta)*b[i](theta)^`'` = r[i, j](theta)](images/IntSurvey_230.gif) .
.
As in rational function integration, apply integration by parts to obtain the Hermite reduction:
/b[i](theta)^j, x) = -t(theta)/((j-1)*b[i](theta)^(j-1))+Int((s(theta)+t(theta)^`'`/(j-1))/b[i](theta)^(j-1), x)](images/IntSurvey_231.gif)
/b[i](theta)^j, x) = -t(theta)/((j-1)*b[i](theta)^(j-1))+Int((s(theta)+t(theta)^`'`/(j-1))/b[i](theta)^(j-1), x)](images/IntSurvey_232.gif)
![]() .
.
Continuing such reductions until no remaining integral has a denominator containing a power ![]() >
> ![]() , we reduce the integration problem to one in which the denominator is square-free.
, we reduce the integration problem to one in which the denominator is square-free.
Rothstein-Trager Theorem: log extension
The problem is to express  where
where ![]() ,
, ![]() is square-free, and where
is square-free, and where ![]() is a logarithmic extension.
is a logarithmic extension.
Theorem 4 (Rothstein-Trager Theorem: log extension)
(i) 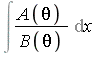 is elementary if and only if all of the roots of
is elementary if and only if all of the roots of
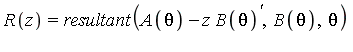
are constants. In other words, the primitive part of ![]() with respect to the variable
with respect to the variable ![]() must have constant coefficients.
must have constant coefficients.
(ii) If 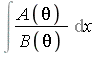 is elementary then
is elementary then
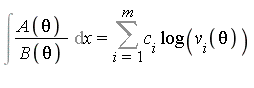
where ![]() are the distinct roots of
are the distinct roots of ![]() and where
and where ![]() are defined by
are defined by
 = gcd(A(theta)-c[i]*B(theta)^`'`, B(theta))](images/IntSurvey_249.gif) .
.
Moreover, this expresses the integral using the minimal algebraic extension field.
Example 1.9
Consider the following integral.
| > | Int(1/ln(x), x); |
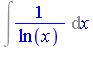
The integrand is 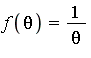 in the function field
in the function field ![]() where
where ![]() .
.
A resultant computation (Rothstein-Trager Theorem) is applicable.
| > | A := 1: B := theta: |
| > | diff_B := diff(ln(x), x); |

| > | R := resultant(A - z*diff_B, B, theta); |
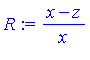
The single root of ![]() is
is ![]() which is not a constant.
which is not a constant.
Therefore the original integral is not elementary.
| > |
Example 1.10
The integral
| > | Int(1/(x*ln(x)), x); |

has integrand 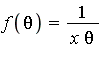 in the function field
in the function field ![]() where
where ![]() .
.
This time, the resultant computation is as follows.
| > | A := 1: B := x*theta: |
| > | diff_B := subs(ln(x)=theta, diff(subs(theta=ln(x), B), x)); |
![]()
| > | R := resultant(A - z*diff_B, B, theta); |
![]()
The single root of ![]() is
is ![]() and the integral is elementary. Specifically,
and the integral is elementary. Specifically,
| > | c[1] := 1; v[1] := gcd(A - c[1]*diff_B, B); |
![]()
![]()
and the integral is
| > | c[1]*ln(v[1]); |
![]()
In other words,
| > | Int(1/(x*ln(x)), x) =
subs(theta=ln(x), c[1]*ln(v[1])); |
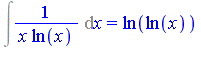
| > |
Polynomial Part (log extension)
For the integration of the "polynomial part", the integrand is a polynomial in the log extension ![]() :
:
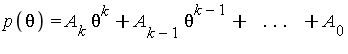
with ![]() in
in ![]() and we can conclude that
and we can conclude that
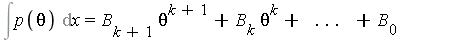

![]() .
.
Note that the last term indicates that some new log extensions may arise.
Differentiating and equating coefficients of powers of the transcendental symbol ![]() , we get:
, we get:
![]()
![A[k] = (k+1)*B[k+1]*theta^`'`+B[k]^`'`](images/IntSurvey_279.gif)
![A[k-1] = k*B[k]*theta^`'`+B[k-1]^`'`](images/IntSurvey_280.gif)
. . .
. . .
![A[1] = 2*B[2]*theta^`'`+B[1]^`'`](images/IntSurvey_281.gif)
![A[0] = B[1]*theta^`'`+(B[0]^`*`)^`'`](images/IntSurvey_282.gif)
where  .
.
We can solve these equations successively, from the top down. At each step there is an integration operation which requires a recursive invocation of the Risch algorithm. This works because the integrand lies in the field ![]() involving one less extension. At any step, if the integral to be computed is not elementary then the algorithm halts with the conclusion that the original integral is not elementary. Moreover, at any step except the last step, if the result of the recursive integration introduces one or more new log extensions then the algorithm halts with the conclusion that the original integral is not elementary. At the last step, new log extensions may appear.
involving one less extension. At any step, if the integral to be computed is not elementary then the algorithm halts with the conclusion that the original integral is not elementary. Moreover, at any step except the last step, if the result of the recursive integration introduces one or more new log extensions then the algorithm halts with the conclusion that the original integral is not elementary. At the last step, new log extensions may appear.
Example 1.11
The integral
![]()
has integrand ![]() in the field
in the field ![]() where
where ![]() . If the integral is elementary then
. If the integral is elementary then
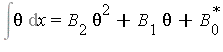
where the equations to be satisfied are
![]()
![1 = 2*B[2]*theta^`'`+B[1]^`'`](images/IntSurvey_291.gif)
![0 = B[1]*theta^`'`+(B[0]^`*`)^`'`](images/IntSurvey_292.gif) .
.
From the first equation we conclude that ![]() , an arbitrary constant of integration. Plugging this into the second equation and integrating both sides yields
, an arbitrary constant of integration. Plugging this into the second equation and integrating both sides yields
![]()
or
![]()
where ![]() is an arbitrary constant of integration. Equating coefficients of
is an arbitrary constant of integration. Equating coefficients of ![]() on both sides of the equation, we conclude that
on both sides of the equation, we conclude that ![]() and
and ![]() .
.
The last equation now becomes
![0 = (x+b[1])*theta^`'`+(B[0]^`*`)^`'`](images/IntSurvey_300.gif)
or rearranging (we always leave the term ![i*b[i]*theta^`'`](images/IntSurvey_301.gif) on the right hand side since integration of this term is trivial):
on the right hand side since integration of this term is trivial):
![-x*theta^`'` = b[1]*theta^`'`+(B[0]^`*`)^`'`](images/IntSurvey_302.gif) .
.
At this point we use the fact that ![]() (i.e.
(i.e. 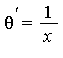 ) on the left hand side, and integrate both sides to get
) on the left hand side, and integrate both sides to get
![]()
from which we conclude (by equating coefficients of ![]() on both sides of the equation) that
on both sides of the equation) that ![]() and
and ![]() , ignoring the arbitrary constant of integration in this final step. Putting it all together we have
, ignoring the arbitrary constant of integration in this final step. Putting it all together we have
| > | theta := ln(x): |
| > | B[2] := 0: B[1] := x: B[0] := -x: |
| > | Int(theta, x) = B[2]*theta^2 + B[1]*theta + B[0]; |
![]()
| > |
Example 1.12
The integral
![]()
has integrand ![]() in the field
in the field ![]() where
where ![]() and
and ![]() . If the integral is elementary then
. If the integral is elementary then
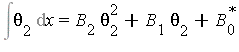
where the equations to be satisfied are
![]()
![1 = 2*B[2]*theta[2]^`'`+B[1]^`'`](images/IntSurvey_317.gif)
![0 = B[1]*theta[2]^`'`+(B[0]^`*`)^`'`](images/IntSurvey_318.gif) .
.
From the first equation we conclude that ![]() , an arbitrary constant of integration. Plugging this into the second equation and integrating both sides yields
, an arbitrary constant of integration. Plugging this into the second equation and integrating both sides yields
![]()
or
![]()
where ![]() is an arbitrary constant of integration. Equating coefficients of
is an arbitrary constant of integration. Equating coefficients of ![]() on both sides of the equation, we conclude that
on both sides of the equation, we conclude that ![]() and
and ![]() . The last equation now becomes
. The last equation now becomes
![0 = (x+b[1])*theta[2]^`'`+(B[0]^`*`)^`'`](images/IntSurvey_326.gif)
or rearranging:
![-x*theta[2]^`'` = b[1]*theta[2]^`'`+(B[0]^`*`)^`'`](images/IntSurvey_327.gif) .
.
Since ![theta[2]^`'` = theta[1]^`'`/theta[1]](images/IntSurvey_328.gif) , i.e.
, i.e. ![theta[2]^`'` = 1/(x*ln(x))](images/IntSurvey_329.gif) , substituting for
, substituting for ![]() on the left hand side and integrating yields
on the left hand side and integrating yields
 .
.
From Example 1.9 we know that the integral appearing here is not elementary. Hence we conclude that ![]() is not elementary.
is not elementary.
Integral of an exponential extension
Suppose that the last extension ![]() is an exponential extension, i.e.
is an exponential extension, i.e. 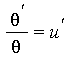 for some function
for some function ![]() in
in ![]() . Applying Euclidean division with remainder yields
. Applying Euclidean division with remainder yields 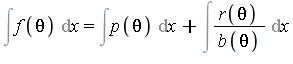 .
.
Unlike the logarithmic case, we must remove any power of ![]() from the denominator on the right hand side, and incorporate it into the new "polynomial part":
from the denominator on the right hand side, and incorporate it into the new "polynomial part": 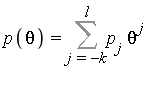 . (This can be done.)
. (This can be done.)
We now have two integrals to consider: (1) the integral of the polynomial part; and (2) the integral of the rational part. Again, task (1) is the harder of the two parts. We first consider task (2).
Hermite Reductions for the Rational Part (exp extension)
This case is very similar to the logarithmic case. Applying square-free factorization of the denominator yields 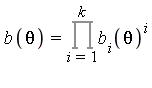 where this means "square-free as a polynomial in
where this means "square-free as a polynomial in ![]() ." For application in subsequent steps of the algorithm, we need to know that the following theorem holds.
." For application in subsequent steps of the algorithm, we need to know that the following theorem holds.
Theorem 5: If ![]() is a monic polynomial which is square-free as a polynomial in the symbol
is a monic polynomial which is square-free as a polynomial in the symbol ![]() and if
and if ![]() for some function
for some function ![]() then
then
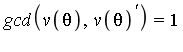
where the latter differentiation is with respect to ![]() , provided that
, provided that ![]() does not divide
does not divide ![]() .
.
Then, exactly as in the logarithmic case, applying partial fraction expansion we get
 where
where ![]() .
.
For each integral with a denominator containing a power ![]() >
> ![]() , apply the Extended Euclidean Algorithm to solve
, apply the Extended Euclidean Algorithm to solve
+t(theta)*b[i](theta)^`'` = r[i, j](theta)](images/IntSurvey_354.gif) .
.
As before, apply integration by parts to obtain the Hermite reduction:
/b[i](theta)^j, x) = -t(theta)/((j-1)*b[i](theta)^(j-1))+Int((s(theta)+t(theta)^`'`/(j-1))/b[i](theta)^(j-1), x)](images/IntSurvey_355.gif)
/b[i](theta)^j, x) = -t(theta)/((j-1)*b[i](theta)^(j-1))+Int((s(theta)+t(theta)^`'`/(j-1))/b[i](theta)^(j-1), x)](images/IntSurvey_356.gif)
![]() .
.
Continuing such reductions until no remaining integral has a denominator containing a power ![]() >
> ![]() , we reduce the integration problem to one in which the denominator is square-free.
, we reduce the integration problem to one in which the denominator is square-free.
Rothstein-Trager Theorem: exp extension
The problem is to express 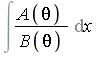 where
where ![]() ,
, ![]() is square-free, and where
is square-free, and where ![]() is an exponential extension.
is an exponential extension.
Theorem 6 (Rothstein-Trager Theorem: exp extension)
(i) 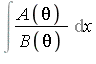 is elementary if and only if all of the roots of
is elementary if and only if all of the roots of
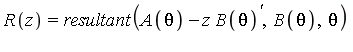
are constants. In other words, the primitive part of ![]() with respect to the variable
with respect to the variable ![]() must have constant coefficients.
must have constant coefficients.
(ii) If 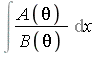 is elementary then
is elementary then
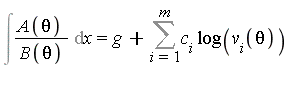
where ![]() are the distinct roots of
are the distinct roots of ![]() ,
, ![]() are defined by
are defined by
 = gcd(A(theta)-c[i]*B(theta)^`'`, B(theta))](images/IntSurvey_373.gif)
and where 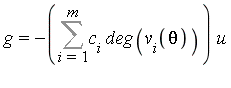 .
.
Moreover, this expresses the integral using the minimal algebraic extension field.
Example 1.13
Consider the following integral.
| > | restart; |
| > | f := (x*exp(2*x^2)+8*sqrt(2)*x*(exp(x^2)+1)+2*x)/
(exp(3*x^2)+exp(2*x^2)+2*exp(x^2)+2): |
| > | Int(f,x); |
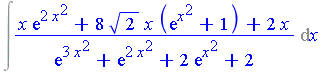
The integrand is 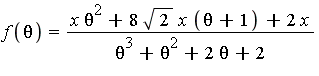 in the function field
in the function field ![]() where
where 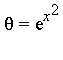 .
.
A resultant computation (Rothstein-Trager Theorem) is applicable.
Keep in mind that ![]() where
where ![]() .
.
| > | u := x^2: |
| > | A := x*theta^2 + 8*sqrt(2)*x*(theta+1) + 2*x: |
| > | B := theta^3 + theta^2 + 2*theta + 2: |
| > | diff_B := subs(exp(u)=theta, diff(subs(theta=exp(u), B), x)); |
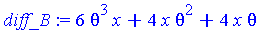
| > | R := resultant(A - z*diff_B, B, theta); |
![]()
| > | solve(R=0, z); |
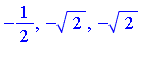
The distinct roots of ![]() are
are 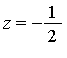 and
and ![]() and the integral is elementary. Specifically,
and the integral is elementary. Specifically,
| > | c[1] := -1/2: c[2] := -sqrt(2): |
| > | v[1] := gcd(A - c[1]*diff_B, B); |
![]()
| > | v[2] := gcd(A - c[2]*diff_B, B); |
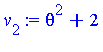
The function ![]() appearing in Theorem 6 is
appearing in Theorem 6 is
| > | g := add(-c[i]*degree(v[i],theta), i=1..2) * u; |
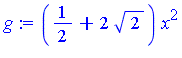
and the desired integral is
| > | result := g + add(c[i]*ln(v[i]), i=1..2); |
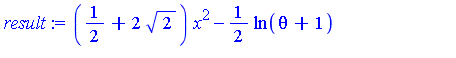

In other words,
| > | Int(f,x) = subs(theta=exp(u), result); |
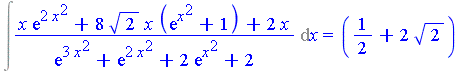
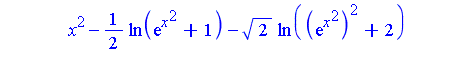
| > |
Polynomial Part (exp extension)
For the integration of the "polynomial part", the integrand is of the form 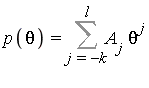 with
with ![]() in
in ![]() , where
, where ![]() is an exponential extension. We can conclude that
is an exponential extension. We can conclude that
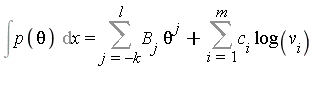 .
.
Note that the latter summation indicates that some new log extensions may arise.
Differentiating and equating coefficients of powers of the transcendental symbol ![]() , we get:
, we get:
![]() , for
, for ![]()
![A[0] = (B[0]^`*`)^`'`](images/IntSurvey_403.gif)
where 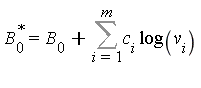 .
.
Solving the latter equation for ![]() requires a recursive integration:
requires a recursive integration: ![]() where the integrand lies in the field
where the integrand lies in the field ![]() . For the general case,
. For the general case, ![]() , the equation to be solved for
, the equation to be solved for ![]() is known as a Risch differential equation. This may sound like a backwards step to have reduced an integration problem to the solution of a differential equation! However, the problem can be solved because we must look for a solution in the field
is known as a Risch differential equation. This may sound like a backwards step to have reduced an integration problem to the solution of a differential equation! However, the problem can be solved because we must look for a solution in the field ![]() only. Nonetheless, this is a difficult problem, in general, for which a complete solution was presented in [Bronstein90a]. See also [Bronstein97].
only. Nonetheless, this is a difficult problem, in general, for which a complete solution was presented in [Bronstein90a]. See also [Bronstein97].
Example 1.14
The integral
| > | restart; |
| > | Int(exp(-x^2), x); |
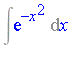
has integrand ![]() in the function field
in the function field ![]() where
where 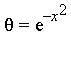 .
.
The solution must take the form ![]() where
where ![]() in
in ![]() is a solution of the Risch differential equation
is a solution of the Risch differential equation ![]() .
.
Since ![]() must be a rational function in
must be a rational function in ![]() , one first argues that it must be a polynomial in
, one first argues that it must be a polynomial in ![]() . This follows because if
. This follows because if ![]() had a nontrivial denominator then
had a nontrivial denominator then ![]() would have a higher-degree denominator and these denominators could not cancel out to correspond to the right hand side of the differential equation which is the constant 1 . So assume that
would have a higher-degree denominator and these denominators could not cancel out to correspond to the right hand side of the differential equation which is the constant 1 . So assume that ![]() is a nonzero polynomial in
is a nonzero polynomial in ![]() with
with ![]() where
where ![]() . But then taking the degree of each side of the differential equation, we get
. But then taking the degree of each side of the differential equation, we get ![]() which is a contradiction. Hence the given Risch differential equation has no solution in the field
which is a contradiction. Hence the given Risch differential equation has no solution in the field ![]() from which we conclude that the original integral is not elementary.
from which we conclude that the original integral is not elementary.
| > |
Comments on algebraic and mixed extensions
In the algorithm presented above we considered only transcendental elementary functions. The Risch algorithm for elementary functions also deals with algebraic extensions. For example, if the integral to be computed is 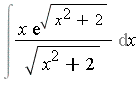 then the integrand lies in the elementary function field
then the integrand lies in the elementary function field ![]() where
where  is an algebraic extension of
is an algebraic extension of ![]() and
and 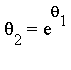 is a transcendental extension of
is a transcendental extension of ![]() . The Risch algorithm proceeds generally in the same manner as discussed above except that there are some different technical details (some of them involving concepts from advanced algebra) for algebraic extensions in the most general case. Some references which discuss the integration of elementary functions for the case of algebraic extensions, and mixed transcendental and algebraic extensions, are [Trager84] and [Bronstein90b].
. The Risch algorithm proceeds generally in the same manner as discussed above except that there are some different technical details (some of them involving concepts from advanced algebra) for algebraic extensions in the most general case. Some references which discuss the integration of elementary functions for the case of algebraic extensions, and mixed transcendental and algebraic extensions, are [Trager84] and [Bronstein90b].
Comments on non-elementary extensions
The power of the Risch algorithm to determine conclusively whether or not a given elementary function has an elementary antiderivative is impressive, in principle. However in most practical problems where the operation of integration arises, it is quite unsatisfactory to receive as a result: "the integral cannot be expressed in elementary terms". For example, the Risch algorithm proves that 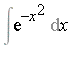 cannot be expressed as an elementary function (see Example 1.14) but in a larger function field the integral can be expressed:
cannot be expressed as an elementary function (see Example 1.14) but in a larger function field the integral can be expressed:
| > | Int(exp(-x^2), x) = int(exp(-x^2), x); |
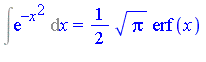
where a special function, the error function, arises. Another case is the following integral which in Example 1.12 was proved to be non-elementary:
| > | Int(ln(ln(x)), x) = int(ln(ln(x)), x); |
![]()
where another special function, the exponential integral, arises.
| > |
It would be ideal if we could extend the elementary function field by an arbitrary number of special functions, as new transcendental extensions, and have a corresponding extended Risch algorithm as a decision procedure for the extended field. At the present time, decision procedures have not been developed for integration in function fields containing many of the commonly-used special functions. However, decision procedures have been developed for some special functions. Early work in this regard is reported in [Cherry85], [Cherry86] where decision procedures are developed for the error function and the logarithmic integral. Additional examples of integrals which can be computed in this context are the following two integrals.
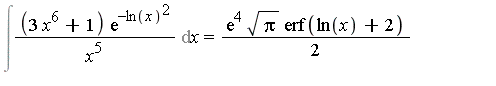
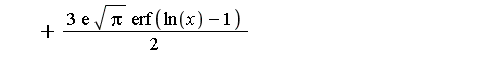
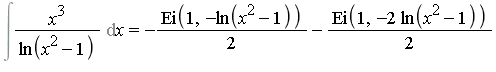
See [Bronstein97] for a presentation of the state-of-the-art of integration algorithms for transcendental functions.
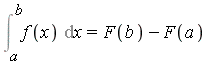 .
. 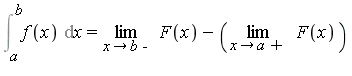 .
. 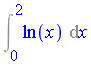
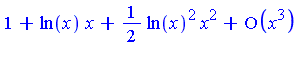
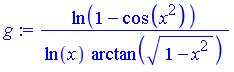
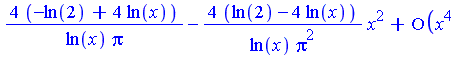
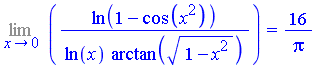

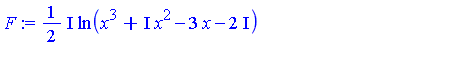


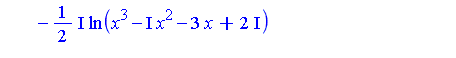
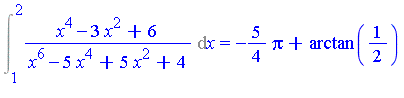
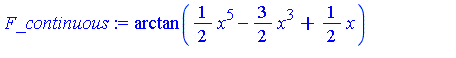
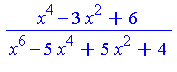
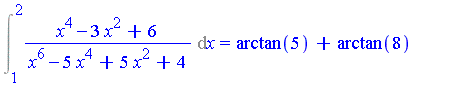
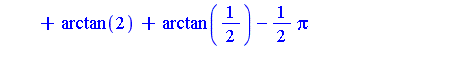
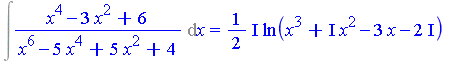
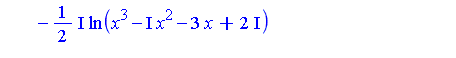
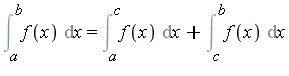

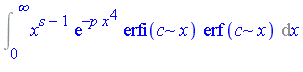
![p^(-1/4*s-1/2)*c^2*hypergeom([1/2, 1, 1/2+1/4*s], [3/4, 5/4, 3/2], 1/4*c^4/p)*GAMMA(1/2+1/4*s)/Pi](images/IntSurvey_501.gif)
![p^(-1/4*s-1/2)*c^2*hypergeom([1/2, 1, 1/2+1/4*s], [3/4, 5/4, 3/2], 1/4*c^4/p)*GAMMA(1/2+1/4*s)/Pi](images/IntSurvey_502.gif)
![p^(-1/4*s-1/2)*c^2*hypergeom([1/2, 1, 1/2+1/4*s], [3/4, 5/4, 3/2], 1/4*c^4/p)*GAMMA(1/2+1/4*s)/Pi](images/IntSurvey_503.gif)
![-I*x^(s-1)*exp(-p*x^4)*MeijerG([[1], []], [[1/2], [0]], -c^2*x^2)*MeijerG([[1], []], [[1/2], [0]], c^2*x^2)/Pi](images/IntSurvey_505.gif)
![-I*x^(s-1)*exp(-p*x^4)*MeijerG([[1], []], [[1/2], [0]], -c^2*x^2)*MeijerG([[1], []], [[1/2], [0]], c^2*x^2)/Pi](images/IntSurvey_506.gif)
![-I*x^(s-1)*exp(-p*x^4)*MeijerG([[1], []], [[1/2], [0]], -c^2*x^2)*MeijerG([[1], []], [[1/2], [0]], c^2*x^2)/Pi](images/IntSurvey_507.gif)
![p^(-1/4*s-1/2)*c^2*hypergeom([1/2, 1, 1/2+1/4*s], [3/4, 5/4, 3/2], 1/4*c^4/p)*GAMMA(1/2+1/4*s)/Pi](images/IntSurvey_510.gif)
![p^(-1/4*s-1/2)*c^2*hypergeom([1/2, 1, 1/2+1/4*s], [3/4, 5/4, 3/2], 1/4*c^4/p)*GAMMA(1/2+1/4*s)/Pi](images/IntSurvey_511.gif)
![1/2*hypergeom([1/2, 1], [3/4, 5/4], 1/4)/Pi^(1/2)](images/IntSurvey_514.gif)
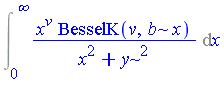

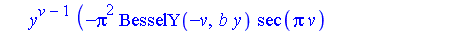
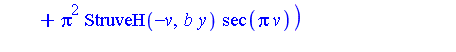
![1/2*x^v*MeijerG([[], []], [[1/2*v, -1/2*v], []], 1/4*b^2*x^2)/(x^2+y^2)](images/IntSurvey_521.gif)
![1/2*x^v*MeijerG([[], []], [[1/2*v, -1/2*v], []], 1/4*b^2*x^2)/(x^2+y^2)](images/IntSurvey_522.gif)