Intersection of Surfaces via Groebner Basis Computation 

>

restart;

 

>	eq[1] := x^2 + y^2 + z^2 = 1;

 

>	eq[2] := x^2 + y^2 + z^2 = 2*x;

 

>	eq[3] := 2*x - 3*y = z;

 

Use plots to see the surfaces represented by these equations in 3-dimensional space. 

>	with(plots):

 

>	implicitplot3d(eq[1], x=-1..1, y=-1..1, z=-1..1, axes=boxed);

 

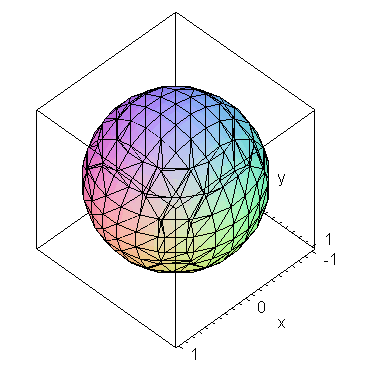
>	implicitplot3d(eq[2], x=-1..1, y=-1..1, z=-1..1, axes=boxed);

 

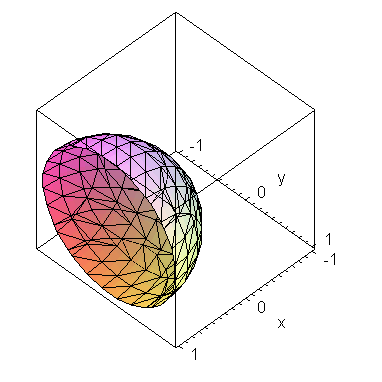
>	implicitplot3d(eq[3], x=-1..1, y=-1..1, z=-1..1, axes=boxed);

 

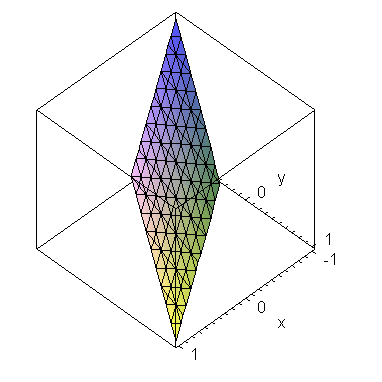
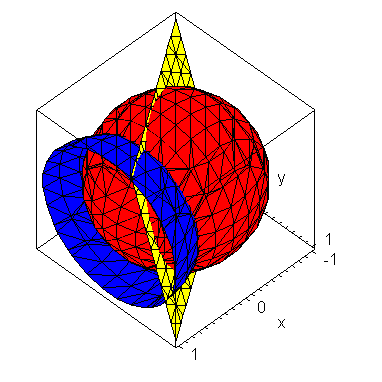
The following command shows all three surfaces in one plot. 

By dragging with the mouse, you can rotate the plot to see different views. 

>	implicitplot3d([eq[1],eq[2],eq[3]], x=-1..1, y=-1..1, z=-1..1,   axes=boxed, color=[red,blue,yellow]);

 

>

 

Problem: 

Find the points of intersection of these three surfaces by using a Groebner basis computation.  Show the Groebner basis that you computed, show the intersection points in explicit form in terms of radicals, and also apply    to show the points in floating-point form. 

>	F := [seq(lhs(eq[i])-rhs(eq[i]), i = 1..3)];

 

>	G := Groebner:-Basis(F, plex(x,y,z));

 

>	_EnvExplicit := true;

 

>	soln := solve(G, [x,y,z]);

 

>	evalf(soln);

 

>