Groebner Bases for Polynomial Systems: A Brief Introduction
K.O. Geddes
Symbolic Computation Group
D.R. Cheriton School of Computer Science
University of Waterloo
Waterloo ON N2L 3G1
CANADA
http://www.uwaterloo.ca/~kogeddes
Abstract
The concept of Groebner bases is introduced using some motivating examples. Two types of applications are considered: (1) canonical forms for polynomials with side relations; and (2) solutions of systems of polynomial equations.
Canonical Forms for Polynomials with Side Relations
Univariate Side Relations
Suppose that we wish to simplify an expression which contains various powers of the symbol  , under the assumption that
, under the assumption that 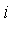 represents the complex number
represents the complex number 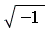 . For example,
. For example,
| > |
e := 4*i^5 - 7*i^4 + i^3 + 3*i^2 - 5*i + 11; |
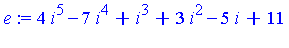
As a naive approach, we could think of applying transformation rules such as:
i^2 --> -1
i^3 --> -i
i^4 --> 1
i^5 --> i
etc.
For the above example, the expression simplifies as follows.
| > |
subs({i^2=-1, i^3=-i, i^4=1, i^5=i}, e); |
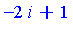
An algorithmic approach to the problem is as follows.
We wish to simplify the expression 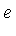 with respect to the following side relation which the variable
with respect to the following side relation which the variable 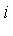 must satisfy:
must satisfy: 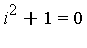 .
.
The given expression lies in a polynomial domain 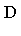 [
[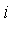 ] over some coefficient domain
] over some coefficient domain 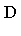 but we really want to represent the expression in a canonical form as an element of the quotient ring
but we really want to represent the expression in a canonical form as an element of the quotient ring ![D[i]/`<,>`(i^2+1)](images/GroebnerIntro_12.gif) -- i.e. as a polynomial modulo the ideal generated by
-- i.e. as a polynomial modulo the ideal generated by 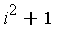 .
.
Question: Is it possible to specify a canonical form for elements of the quotient ring ![D[i]/`<,>`(i^2+1)](images/GroebnerIntro_14.gif) ?
?
Yes it is possible. Any element of the quotient ring can be represented uniquely in terms of the basis  -- i.e. as a polynomial of degree 1 in the variable
-- i.e. as a polynomial of degree 1 in the variable 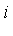 .
.
Algorithm to Transform an Expression into Canonical Form
For the quotient ring discussed above, transformation to canonical form can be obtained by applying Euclidean division with remainder:
 -->
--> 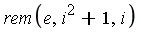 .
.
Example 1
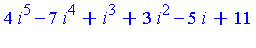
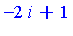
Of course, Maple will automatically simplify expressions involving 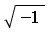 which has the alias
which has the alias  in Maple.
in Maple.
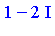
Example 2
The above discussion applies to any univariate side relation.
As a second example, consider an expression in the symbol 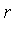 which represents
which represents 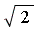 .
.
In this case, the side relation satisfied by the symbol 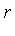 is:
is: 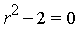 .
.
| > |
f := r^6 - 5/7*r^5 + 23*r^4 + 1/2*r^3 - 35/11*r^2 + r - 1/2; |
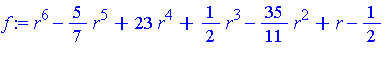
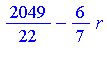
Again, Maple will automatically simplify expressions involving 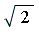 .
.

Multivariate Side Relations
Suppose, for example, that we have a trigonometric expression involving 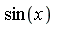 and
and 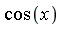 and we wish to simplify the expression with respect to the following side relation:
and we wish to simplify the expression with respect to the following side relation: 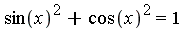 .
.
We can choose to think of this as a polynomial side relation 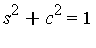 and to represent
and to represent 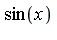 and
and 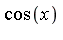 in the expression by the symbols
in the expression by the symbols 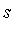 and
and  , respectively. We are then faced with the problem of simplifying a multivariate polynomial with respect to a multivariate side relation.
, respectively. We are then faced with the problem of simplifying a multivariate polynomial with respect to a multivariate side relation.
Expressing this in the notation of algebra, the original expression lies in a bivariate polynomial domain 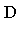 [
[ ] and we wish to express it (in a canonical form, if possible) as an element of the quotient ring
] and we wish to express it (in a canonical form, if possible) as an element of the quotient ring ![D[s, t]/`<,>`(s^2+c^2-1)](images/GroebnerIntro_42.gif) .
.
Question: Is it possible to specify a canonical form for elements of the quotient ring ![D[s, t]/`<,>`(s^2+c^2-1)](images/GroebnerIntro_43.gif) ?
?
The answer is not obvious.
For example, the following expressions are mathematically equivalent:
| > |
e1 := sin(x)^2 * cos(x)^2; |
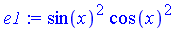
| > |
e2 := expand( subs(cos(x)^2 = 1-sin(x)^2, e1) ); |
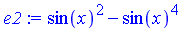
| > |
e3 := expand( subs(sin(x)^2 = 1-cos(x)^2, e1) ); |
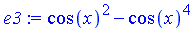
Which form is "best"? "simplest"? It depends on your point of view.
The more general Question is: Given a multivariate polynomial domain 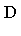 [
[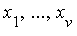 ] and one or more side relations
] and one or more side relations 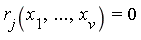 (
(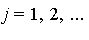 ), is it possible to specify a canonical form for elements of the quotient ring
), is it possible to specify a canonical form for elements of the quotient ring 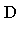 [
[ ] /
] / 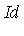 where
where 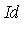 is the ideal generated by the polynomials
is the ideal generated by the polynomials 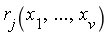 ?
?
Until the 1960s it was not known whether this question could be answered in the affirmative. It turns out that the answer is Yes, via the theory of Groebner bases.
Maple syntax for simplification w.r.t. side relations
Before proceeding further, consider a Maple example. For the simplification of expressions modulo side relations in Maple, see the help page ?simplify[siderels] .
The syntax of the command is 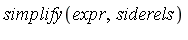 where
where 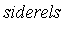 is a set of one or more side relations. When the simplify command is invoked in this form, Maple applies the theory of Groebner bases. Specifically, a Groebner basis for
is a set of one or more side relations. When the simplify command is invoked in this form, Maple applies the theory of Groebner bases. Specifically, a Groebner basis for 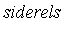 is computed and then
is computed and then 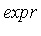 is reduced modulo this Groebner basis by transformations to be described in a subsequent section.
is reduced modulo this Groebner basis by transformations to be described in a subsequent section.
Note: This yields a canonical form. But which canonical form? It depends on the choice of ordering for the variables. The user can control the ordering by using the 3-argument syntax 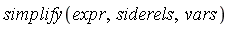 where
where 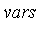 is a list of variables in the desired order.
is a list of variables in the desired order.
Example 3
| > |
siderels := {sin(x)^2 + cos(x)^2 = 1}; |
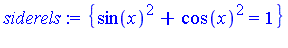
| > |
e := sin(x)^3 - 11*sin(x)^2*cos(x) + 3*cos(x)^3 - sin(x)*cos(x) + 2; |

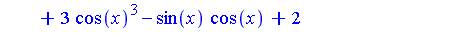
The following command indicates that we wish to "favour" transforming cos(x) into sin(x) as much as possible.
| > |
simplify(e, siderels, [cos(x),sin(x)]); |
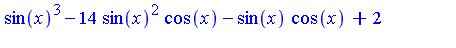

The following command indicates that we wish to "favour" transforming sin(x) into cos(x) as much as possible.
| > |
simplify(e, siderels, [sin(x),cos(x)]); |
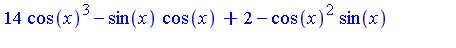

Try simplifying the following expression  .
.
| > |
f := sin(x)^2 * cos(x)^2; |
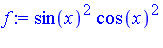
| > |
simplify(f, siderels, [cos(x),sin(x)]); |
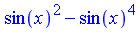
| > |
simplify(f, siderels, [sin(x),cos(x)]); |
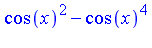
The expression 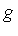 is equivalent to zero, and therefore its canonical form must be 0 (regardless of ordering).
is equivalent to zero, and therefore its canonical form must be 0 (regardless of ordering).
| > |
g := f - sin(x)^2 + sin(x)^4; |
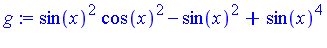
Groebner Basis Preliminaries
Consider the polynomial domain Q[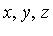 ] in three variables over the field Q of rational numbers. Suppose that the following three side relations are specified.
] in three variables over the field Q of rational numbers. Suppose that the following three side relations are specified.
| > |
siderels := {x^3*y*z = x*z^2, x*y^2*z = x*y*z, x^2*y^2 = z^2}; |
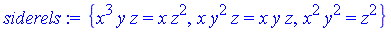
Consider the following polynomial expression.
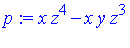
Problem: Express 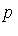 in a canonical form with respect to
in a canonical form with respect to 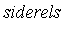 .
.
This can be accomplished in Maple as follows.

Offhand, you would not be able to recognize that 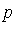 is equivalent to zero. How would you proceed to try to "reduce"
is equivalent to zero. How would you proceed to try to "reduce"  with respect to the given side relations?
with respect to the given side relations?
The mathematical framework is as follows. In the original polynomial domain Q[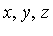 ] we can specify a "vector space" basis for this domain. There are various orderings of the monomials which can be chosen. For the moment, let us choose a basis corresponding to the total degree ordering with monomials of the same total degree ordered by a particular lexicographical ordering (called inverse lexicographical order), as follows.
] we can specify a "vector space" basis for this domain. There are various orderings of the monomials which can be chosen. For the moment, let us choose a basis corresponding to the total degree ordering with monomials of the same total degree ordered by a particular lexicographical ordering (called inverse lexicographical order), as follows.
| > |
tdegBasis := [1,z,y,x,z^2,y*z,x*z,y^2,x*y,x^2,z^3,y*z^2,x*z^2,y^2*z,x*y*z,x^2*z,y^3,x*y^2,x^2*y,x^3,z^4,` . . . `]; |
![[1, z, y, x, z^2, y*z, x*z, y^2, x*y, x^2, z^3, y*z^2, x*z^2, y^2*z, x*y*z, x^2*z, y^3, x*y^2, x^2*y, x^3, z^4, ` . . . `]](images/GroebnerIntro_85.gif)
![[1, z, y, x, z^2, y*z, x*z, y^2, x*y, x^2, z^3, y*z^2, x*z^2, y^2*z, x*y*z, x^2*z, y^3, x*y^2, x^2*y, x^3, z^4, ` . . . `]](images/GroebnerIntro_86.gif)
Given the polynomial expression 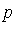 in the domain Q[
in the domain Q[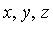 ] , we are required to simplify
] , we are required to simplify 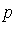 with respect to
with respect to 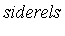 ; in other words, we want to express
; in other words, we want to express 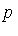 in a canonical form as an element of the quotient ring Q[
in a canonical form as an element of the quotient ring Q[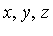 ] /
] / 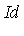 where
where 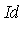 is the ideal generated by the side relations. For
is the ideal generated by the side relations. For 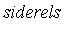 as specified above, the corresponding ideal is
as specified above, the corresponding ideal is
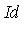 = <
= < 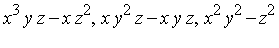 > .
> .
Objective: Define a basis for the quotient ring Q[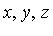 ] /
] / 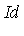 and specify an algorithm to express any particular polynomial
and specify an algorithm to express any particular polynomial 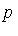 in terms of that basis.
in terms of that basis.
The basis 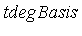 specified above for the domain Q[
specified above for the domain Q[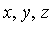 ] clearly is not a basis for the quotient ring. The monomials are not all independent in the quotient ring; e.g.,
] clearly is not a basis for the quotient ring. The monomials are not all independent in the quotient ring; e.g.,  .
.
Question: Which monomials should be deleted from 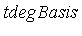 in order to obtain a basis for the quotient ring?
in order to obtain a basis for the quotient ring?
To answer this question, we proceed as follows.
Step 1: Compute a Groebner basis for the ideal 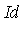 .
.
Step 2: Examine each monomial 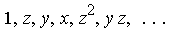 with respect to the Groebner basis for
with respect to the Groebner basis for 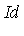 to determine whether, as an element of Q[
to determine whether, as an element of Q[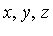 ] /
] /  , it can be reduced to a lower-order monomial (with respect to the specified ordering of monomials). (E.g.,
, it can be reduced to a lower-order monomial (with respect to the specified ordering of monomials). (E.g.,  reduces to
reduces to 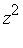 .)
.)
Note: The above concept is vague at this moment, but we will make it more precise. Also, it should be noted that what we will do, in practice, is to apply the reductions indicated in Step 2 on each particular term in the polynomial 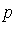 that we wish to simplify.
that we wish to simplify.
Some Remarks about Groebner Bases
The terminology "basis" used in the context of a Groebner basis is not the concept of a "vector space" or "polynomial" basis. Specifically, the elements in the basis will not be linearly independent in the sense of a vector space basis. Rather, it is the concept of an "ideal basis" which means a "set of generators for the ideal". Indeed, for the ideal
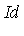 = <
= < 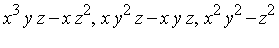 >
>
the corresponding Groebner basis will have more elements (i.e. more generators) than the three specified in the original definition of 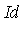 . Using Maple, we can determine a Groebner basis
. Using Maple, we can determine a Groebner basis 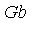 for the ideal
for the ideal 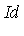 as seen in the following Example.
as seen in the following Example.
(Note that the ideal is represented by specifying the generators in a Maple list. The "angle bracket" notation used above is a common mathematical notation for ideals, but angle brackets in Maple are used for a different purpose.)
Example 4
| > |
Id := [x^3*y*z - x*z^2, x*y^2*z - x*y*z, x^2*y^2 - z^2]; |
![[x^3*y*z-x*z^2, x*y^2*z-x*y*z, x^2*y^2-z^2]](images/GroebnerIntro_118.gif)

| > |
TermOrder := tdeg(x,y,z); |
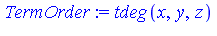
| > |
Gb := Groebner:-Basis(Id, TermOrder); |
![[y*z^3-z^3, -x*z^2+x*z^3, y*x*z^2-x*z^2, -z^4+x^2*z^2, x*y^2*z-x*y*z, -z^3+x^2*y*z, x^2*y^2-z^2, z^5-z^4]](images/GroebnerIntro_121.gif)
![[y*z^3-z^3, -x*z^2+x*z^3, y*x*z^2-x*z^2, -z^4+x^2*z^2, x*y^2*z-x*y*z, -z^3+x^2*y*z, x^2*y^2-z^2, z^5-z^4]](images/GroebnerIntro_122.gif)
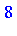
Note that the original specification of the ideal 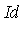 has 3 generators whereas the Groebner basis
has 3 generators whereas the Groebner basis 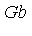 has 8 generators.
has 8 generators.
However, the same ideal is being specified with different sets of generators: 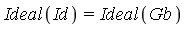 .
.
(See the definition of a Groebner basis in the next section.)
For the polynomial 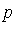 specified above, our task now is to reduce
specified above, our task now is to reduce  with respect to the Groebner basis
with respect to the Groebner basis 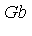 . The function NormalForm in the Groebner package performs "reduction to normal form" of a given polynomial with respect to a particular specification of an ideal. (See the next section for details of the reduction process.)
. The function NormalForm in the Groebner package performs "reduction to normal form" of a given polynomial with respect to a particular specification of an ideal. (See the next section for details of the reduction process.)
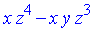
| > |
Groebner:-NormalForm(p, Gb, TermOrder); |

If the original list of generators 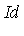 was used to specify the ideal then the reduction process applied by the NormalForm function would fail to recognize that
was used to specify the ideal then the reduction process applied by the NormalForm function would fail to recognize that 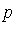 reduces to zero modulo the ideal.
reduces to zero modulo the ideal.
| > |
Groebner:-NormalForm(p, Id, TermOrder); |
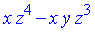
Definition of a Groebner Basis
Definition 1
The S-polynomial of two polynomials 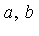 is defined by
is defined by

where 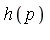 denotes the "head term" of a polynomial
denotes the "head term" of a polynomial  , meaning the leading monomial (with respect to a specified term ordering).
, meaning the leading monomial (with respect to a specified term ordering).
An important property of 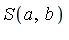 is that the head term of
is that the head term of 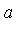 will be eliminated in the case where
will be eliminated in the case where 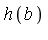 |
| 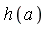 , in which case we have
, in which case we have
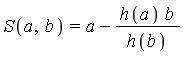 .
.
Example 5
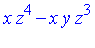
Let's choose one particular element from the Groebner basis 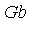 .
.
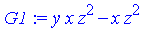
With  and
and 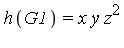 we see that
we see that 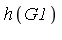 |
| 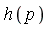 . Hence the
. Hence the 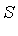 -polynomial
-polynomial 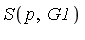 is as follows.
is as follows.
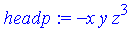
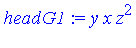
| > |
S := (headG1*p - headp*G1) / gcd(headp,headG1): |
| > |
S := normal(S,expanded); |
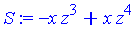
or equivalently,
| > |
S := p - (headp/headG1)*G1; |
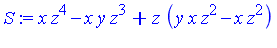

The point to be noted in the above example is that the computation of the 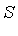 -polynomial
-polynomial 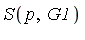 results in a reduction of
results in a reduction of 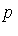 in the following sense:
in the following sense:
- The computed polynomial
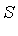 is equivalent to
is equivalent to 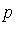 in the quotient ring Q[
in the quotient ring Q[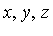 ] /
] / 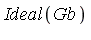 (equivalently, Q[
(equivalently, Q[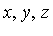 ] /
] / 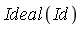 ) because all we did was to subtract from
) because all we did was to subtract from 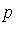 a multiple of
a multiple of 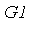 , which is an element of the ideal (i.e.
, which is an element of the ideal (i.e. 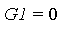 ). Moreover, the head term
). Moreover, the head term 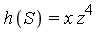 is smaller (in the specified term ordering) than the original head term
is smaller (in the specified term ordering) than the original head term 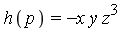 .
.
It is precisely this type of reduction of the terms in the polynomial  that we wish to perform, and we wish to be guaranteed that
that we wish to perform, and we wish to be guaranteed that 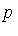 will get reduced to a canonical form. The desired guarantee comes from the definition of a Groebner basis for the ideal.
will get reduced to a canonical form. The desired guarantee comes from the definition of a Groebner basis for the ideal.
Definition 2
A polynomial 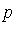 is F-reduced modulo the ideal basis
is F-reduced modulo the ideal basis 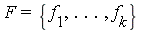 if no head term
if no head term 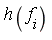 divides
divides 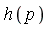 , for
, for 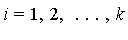 .
.
Method of F-reduction: If 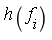 |
| 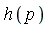 then replace
then replace 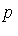 by the
by the 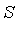 -polynomial
-polynomial ![S(p, f[i])](images/GroebnerIntro_183.gif) . I.e., perform the reduction
. I.e., perform the reduction 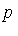 -->
--> ![S(p, f[i])](images/GroebnerIntro_185.gif) . Continue performing reductions until Definition 2 is satisfied.
. Continue performing reductions until Definition 2 is satisfied.
It is clear that if a polynomial 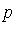
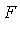 -reduces to zero then
-reduces to zero then 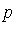 is in
is in 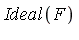 . We would like the converse implication to hold. That is, we would have an effective method to answer the ideal membership question if, for an ideal basis
. We would like the converse implication to hold. That is, we would have an effective method to answer the ideal membership question if, for an ideal basis 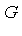 , we would have the property:
, we would have the property:
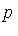 is in
is in 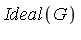 if and only if
if and only if 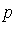
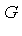 -reduces to zero.
-reduces to zero.
This property is precisely what a Groebner basis gives us.
Definition 3
A set of polynomials 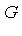 in a polynomial domain
in a polynomial domain 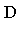 [
[ ] is a Groebner basis (with respect to a specified term ordering) if
] is a Groebner basis (with respect to a specified term ordering) if
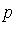 is in
is in 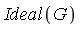 if and only if
if and only if 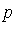
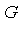 -reduces to 0 .
-reduces to 0 .
An equivalent definition is provided by the following theorem, which tells us that for a Groebner basis  the process of
the process of 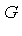 -reduction produces a unique canonical form.
-reduction produces a unique canonical form.
Theorem 1
A set of polynomials 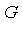 in a polynomial domain
in a polynomial domain 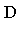 [
[ ] is a Groebner basis if and only if the following property holds:
] is a Groebner basis if and only if the following property holds:

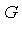 -reduces to
-reduces to 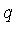 and
and 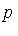
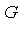 -reduces to
-reduces to 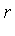 implies
implies 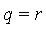 .
.
Concluding Remarks on Computing Groebner Bases
For a detailed development of Buchberger's algorithm to compute a Groebner basis, see [1]. The general idea is that, given an ideal basis 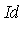 , we must compute another ideal basis
, we must compute another ideal basis 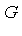 such that
such that 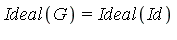 and
and  is a Groebner basis. The algorithm consists of a sequence of operations based on computing
is a Groebner basis. The algorithm consists of a sequence of operations based on computing 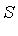 -polynomials and applying the process of
-polynomials and applying the process of 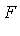 -reduction.
-reduction.
The known algorithms for computing a Groebner basis have time complexity which is exponential in the number of variables. Therefore, if there are too many variables the computation becomes "hopeless". However, for many reasonably-sized problems, the method has proved to be very useful.
As mentioned above, we can answer the general ideal membership question once we have computed a Groebner basis 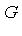 for the ideal. Specifically, to determine whether a given polynomial
for the ideal. Specifically, to determine whether a given polynomial 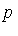 is a member of
is a member of 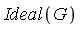 we simply apply
we simply apply  -reductions to determine whether
-reductions to determine whether 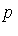
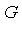 -reduces to zero. In Maple's Groebner package, the NormalForm function can be used for this purpose.
-reduces to zero. In Maple's Groebner package, the NormalForm function can be used for this purpose.
Example 6
Consider the polynomial domain Q[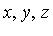 ] and the ideal
] and the ideal  specified above.
specified above.
![[x^3*y*z-x*z^2, x*y^2*z-x*y*z, x^2*y^2-z^2]](images/GroebnerIntro_228.gif)
The Groebner basis for 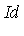 was determined to be as follows.
was determined to be as follows.
![[y*z^3-z^3, -x*z^2+x*z^3, y*x*z^2-x*z^2, -z^4+x^2*z^2, x*y^2*z-x*y*z, -z^3+x^2*y*z, x^2*y^2-z^2, z^5-z^4]](images/GroebnerIntro_230.gif)
![[y*z^3-z^3, -x*z^2+x*z^3, y*x*z^2-x*z^2, -z^4+x^2*z^2, x*y^2*z-x*y*z, -z^3+x^2*y*z, x^2*y^2-z^2, z^5-z^4]](images/GroebnerIntro_231.gif)
Let 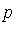 be the polynomial defined above. Is
be the polynomial defined above. Is 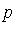 in
in 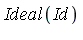 ?
?
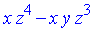
| > |
Groebner:-NormalForm(p, Gb, TermOrder); |
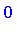
Since 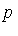
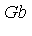 -reduces to zero we conclude that
-reduces to zero we conclude that 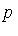 is in
is in 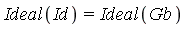 .
.
Create two different polynomials 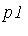 and
and 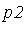 which are known to be equivalent modulo
which are known to be equivalent modulo 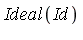 .
.
| > |
q := 3*x^5*y*z^2 - 1/2*x^4*y^3 + x*y*z; |
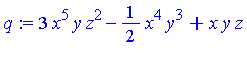
| > |
p1 := expand(q + (x^2 + y^2 + z^2)*p); |
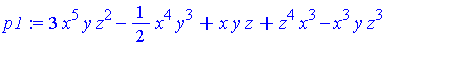
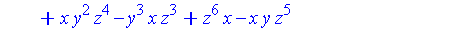
| > |
p2 := expand(q + (x^3*y^2 - 3/4*x^2*z + 1/4*x*z^3 - 4/5)*p); |
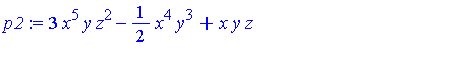
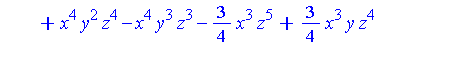
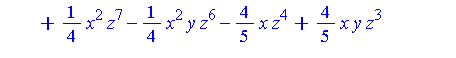
Applying NormalForm to each of  and
and 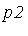 should
yield the same canonical form.
should
yield the same canonical form.
| > |
Groebner:-NormalForm(p1, Gb, TermOrder); |
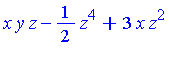
| > |
Groebner:-NormalForm(p2, Gb, TermOrder); |

This must also be the canonical form of the polynomial 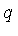 .
.
| > |
Groebner:-NormalForm(q, Gb, TermOrder); |
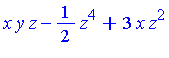
Solving Systems of Polynomial Equations
In this section we note, by looking at some examples, that a Groebner basis can be a very powerful tool for the problem of computing solutions to systems of polynomial equations. Specifically, the term ordering which is most desirable for this application is pure lexicographical ordering . For example, in the polynomial domain Q[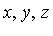 ] the pure lexicographical ordering implies
] the pure lexicographical ordering implies
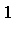 <
< 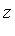 <
< 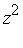 <
<  <
< 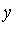 <
< 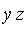 <
<  <
<  <
< 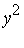 <
< 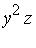 <
< 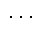 <
<  <
< 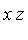 <
<  <
< 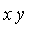 <
<  .
.
The Problem
Given a system of polynomial equations


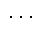
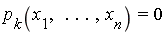
we wish to find values of ( 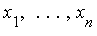 ) which simultaneously satisfy the
) which simultaneously satisfy the 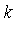 polynomial equations.
polynomial equations.
Solution Technique
Consider 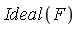 , the ideal generated by the given polynomials
, the ideal generated by the given polynomials 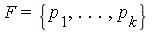 , and compute its Groebner basis
, and compute its Groebner basis 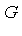 using pure lexicographical ordering. Then the set of common zeros of
using pure lexicographical ordering. Then the set of common zeros of 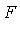 is identical to the set of common zeros of
is identical to the set of common zeros of 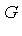 and, moreover, we can obtain much more information about the common zeros from
and, moreover, we can obtain much more information about the common zeros from 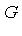 than from the original polynomials
than from the original polynomials 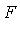 .
.
Example 7
Suppose that we wish to solve the three polynomial equations: 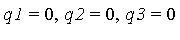 defined as follows.
defined as follows.
| > |
q1 := x^2*y + 4*y^2 - 17: |
| > |
q2 := 2*x*y - 3*y^3 + 8: |
| > |
q3 := x*y^2 - 5*x*y + 1: |
![[x^2*y+4*y^2-17, 2*x*y-3*y^3+8, x*y^2-5*x*y+1]](images/GroebnerIntro_287.gif)
| > |
G := Groebner:-Basis(F, plex(x,y,z)); |
![[1]](images/GroebnerIntro_288.gif)
The system of equations specified by the Groebner basis is 1 = 0 which has no solution. Therefore the original set of polynomial equations has no solution.
Example 8
Suppose that we wish to solve the following system of three polynomials.
![[x^2+y*z-2, y^2+x*z-3, x*y+z^2-5]](images/GroebnerIntro_289.gif)
| > |
G := Groebner:-Basis(F, plex(x,y,z)); |
![[8*z^8+438*z^4-760*z^2+361-100*z^6, 361*y+52*z^5-740*z^3+1425*z+8*z^7, 361*x-88*z^7-2690*z^3+2375*z+872*z^5]](images/GroebnerIntro_290.gif)
![[8*z^8+438*z^4-760*z^2+361-100*z^6, 361*y+52*z^5-740*z^3+1425*z+8*z^7, 361*x-88*z^7-2690*z^3+2375*z+872*z^5]](images/GroebnerIntro_291.gif)
![[8*z^8+438*z^4-760*z^2+361-100*z^6, 361*y+52*z^5-740*z^3+1425*z+8*z^7, 361*x-88*z^7-2690*z^3+2375*z+872*z^5]](images/GroebnerIntro_292.gif)
![[8*z^8+438*z^4-760*z^2+361-100*z^6, 361*y+52*z^5-740*z^3+1425*z+8*z^7, 361*x-88*z^7-2690*z^3+2375*z+872*z^5]](images/GroebnerIntro_293.gif)
From the original system of polynomials it is difficult to determine information about the solutions. However, the system of polynomial equations specified by the Groebner basis has a very interesting structure: the system has been triangularized ! Namely, in one equation the variable 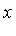 is isolated as a function of
is isolated as a function of 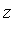 ; in another equation the variable
; in another equation the variable 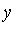 is isolated as a function of
is isolated as a function of 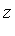 ; and the remaining equation involves a univariate polynomial in the variable
; and the remaining equation involves a univariate polynomial in the variable 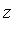 . Therefore, the solutions can be described as follows.
. Therefore, the solutions can be described as follows.
| > |
xpoly := select(has, G, x)[]; |
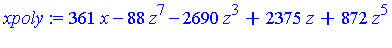
| > |
ypoly := select(has, G, y)[]; |
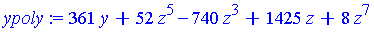
| > |
zpoly := remove(has, G, {x,y})[]; |

We can solve explicitly for 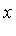 and
and 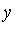 as a function of
as a function of  .
.
| > |
xval := solve(xpoly, x); |
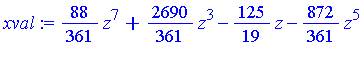
| > |
yval := solve(ypoly, y); |
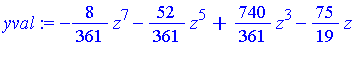
For each of the 8 roots of the univariate polynomial 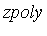 we have a triple (
we have a triple ( 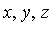 ) which is a solution of the original system of polynomial equations.
) which is a solution of the original system of polynomial equations.
The symbolic representation of the roots of 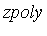 obtained via
obtained via 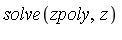 is expressed using the
is expressed using the  construct (by default) and is not very informative. One can note that
construct (by default) and is not very informative. One can note that  is actually just a quartic polynomial in
is actually just a quartic polynomial in 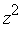 and therefore an explicit symbolic representation of its roots in terms of radicals can be obtained -- the following Maple commands will express the roots in terms of radicals.
and therefore an explicit symbolic representation of its roots in terms of radicals can be obtained -- the following Maple commands will express the roots in terms of radicals.
| > |
# _EnvExplicit := true; |
These commands are commented out here because the resulting expressions for the eight roots are somewhat complicated.
However, we already have a complete structural specification for the solutions of the given system of polynomial equations. We may choose to do numerical root-finding for the roots of 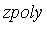 .
.
| > |
zval := fsolve(zpoly, z, 'complex'); |
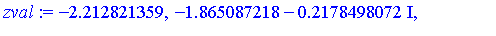
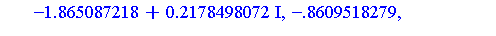
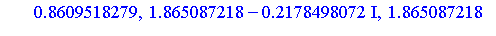
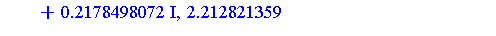
The eight solutions of the original polynomial system 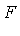 can be computed as follows.
can be computed as follows.
| > |
soln := seq( [x = eval(xval, z=zval[i]),
y = eval(yval, z=zval[i]),
z = zval[i]],
i = 1..nops([zval]) ); |
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_320.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_321.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_322.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_323.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_324.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_325.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_326.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_327.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_328.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_329.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_330.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_331.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_332.gif)
![[x = -1.3530952, y = -0.76433386e-1, z = -2.212821359], [x = -.74633665+.95129733*I, y = -1.329681784-.6060334205*I, z = -1.865087218-.2178498072*I], [x = -.74633665-.95129733*I, y = -1.329681784+.606...](images/GroebnerIntro_333.gif)
Check that each of these eight triples is a zero of the original polynomial system (to the numerical accuracy being used).
| > |
seq( eval(F,soln[i]), i=1..nops([soln]) ); |
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_334.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_335.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_336.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_337.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_338.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_339.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_340.gif)
![[0.49e-7, 0.21e-7, 0.15e-7], [0.21e-7-0.18e-7*I, 0.26e-7+0.4e-8*I, 0.15e-7+0.37e-8*I], [0.21e-7+0.18e-7*I, 0.26e-7-0.4e-8*I, 0.15e-7-0.37e-8*I], [-0.4e-8, 0.5e-8, 0.1e-8], [-0.4e-8, 0.5e-8, 0.1e-8], [...](images/GroebnerIntro_341.gif)
Example 9
In some cases, the Groebner basis for a polynomial system may contain one or more polynomials which can be factored, in which case the polynomial system breaks into subsystems (corresponding to subvarieties in the solution space). The Solve function in the Groebner package is designed to perform factoring whenever possible while computing the lexicographic Groebner basis, so as to facilitate solving the polynomial system. Hence it is advisable to use the Groebner:-Solve function rather than the more basic Groebner:-Basis function when the objective is to solve a system of polynomial equations.
Consider the following system of polynomials.
| > |
f1 := 4*x^2 + x*y^2 - z + 1/4: |
| > |
f2 := 2*x + y^2*z + 1/2: |
| > |
f3 := x^2*z - 1/2*x - y^2: |
![[4*x^2+x*y^2-z+1/4, 2*x+z*y^2+1/2, z*x^2-1/2*x-y^2]](images/GroebnerIntro_342.gif)
| > |
s := Groebner:-Solve(F, [x,y,z]); |
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_343.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_344.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_345.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_346.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_347.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_348.gif)
![{[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}], [[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*...](images/GroebnerIntro_349.gif)
The result  consists of a set of two subsystems, as follows.
consists of a set of two subsystems, as follows.
![[[z-1, 2*y^2-1, 2*x+1], plex(x, y, z), {}]](images/GroebnerIntro_351.gif)
![[[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382], plex(x, y, z), {}]](images/GroebnerIntro_352.gif)
![[[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382], plex(x, y, z), {}]](images/GroebnerIntro_353.gif)
![[[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382], plex(x, y, z), {}]](images/GroebnerIntro_354.gif)
![[[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382], plex(x, y, z), {}]](images/GroebnerIntro_355.gif)
![[[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382], plex(x, y, z), {}]](images/GroebnerIntro_356.gif)
The notation for each subsystem is a list of three elements: a list of polynomials which is a Groebner basis for the subsystem, the term ordering which was used, and the last element is a set of constraints in the form of polynomials which must not vanish.
Note that the simpler of the two subsystems contains a polynomial in 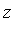 of degree
of degree 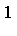 . Let
. Let 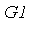 be the Groebner basis of the simpler subsystem and let
be the Groebner basis of the simpler subsystem and let 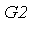 be the Groebner basis of the more complicated subsystem.
be the Groebner basis of the more complicated subsystem.
| > |
(G1,G2) := (s[1][1], s[2][1]): |
| > |
if not member(z-1, G1) then
# Make G1 be the simpler subsystem.
(G1,G2) := (G2,G1)
end if: |
![[z-1, 2*y^2-1, 2*x+1]](images/GroebnerIntro_361.gif)
![[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382]](images/GroebnerIntro_362.gif)
![[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382]](images/GroebnerIntro_363.gif)
![[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382]](images/GroebnerIntro_364.gif)
![[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382]](images/GroebnerIntro_365.gif)
![[16*z^6+8*z^5+9*z^4+61*z^3+136*z^2-206*z+60, 284*y^2+5664*z^5+5568*z^4+5866*z^3+24365*z^2+59937*z-43978, 568*x-2736*z^5-2680*z^4-2771*z^3-11793*z^2-28946*z+21382]](images/GroebnerIntro_366.gif)
From 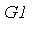 we obtain two solutions.
we obtain two solutions.
| > |
G1_soln := solve(G1, [x,y,z]); |
![[[x = -1/2, y = 1/2*2^(1/2), z = 1], [x = -1/2, y = -1/2*2^(1/2), z = 1]]](images/GroebnerIntro_368.gif)
![[[x = -1/2, y = 1/2*2^(1/2), z = 1], [x = -1/2, y = -1/2*2^(1/2), z = 1]]](images/GroebnerIntro_369.gif)
From 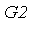 , first separate out the three Groebner basis polynomials.
, first separate out the three Groebner basis polynomials.
| > |
xpoly := select(has, G2, x)[]; |
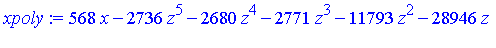

| > |
ypoly := select(has, G2, y)[]; |


| > |
zpoly := remove(has, G2, {x,y})[]; |
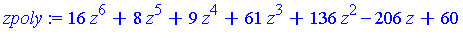
There is one value of 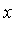 corresponding to each value of
corresponding to each value of  .
.
| > |
xval := solve(xpoly, x); |
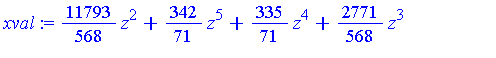

There are two values of 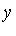 corresponding to each value of
corresponding to each value of 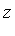 .
.
| > |
yval := solve(ypoly, y); |

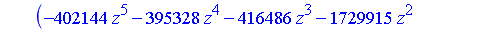
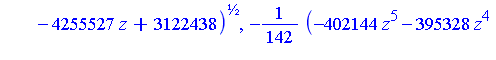

There are six values of 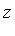 to be determined
to be determined
| > |
zval := solve(zpoly, z); |
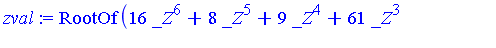
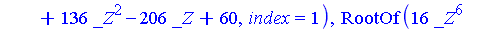

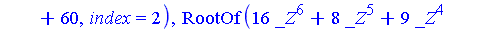
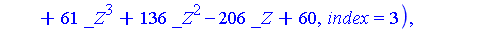


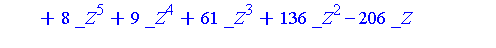
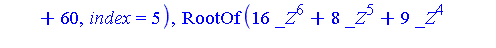
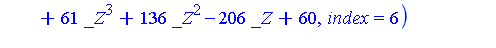
Let us express the 12 solutions corresponding to subsystem 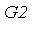 numerically.
numerically.
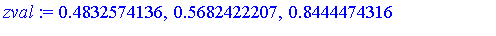


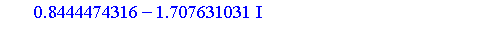
| > |
for i to nops([zval]) do
zi := zval[i];
G2_soln := G2_soln,
[x=eval(xval,z=zi), y=eval(yval[1],z=zi), z=zi],
[x=eval(xval,z=zi), y=eval(yval[2],z=zi), z=zi]
end do: |
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_402.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_403.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_404.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_405.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_406.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_407.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_408.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_409.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_410.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_411.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_412.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_413.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_414.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_415.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_416.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_417.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_418.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_419.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_420.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_421.gif)
![[x = -7.23329154, y = 5.375957437, z = .4832574136], [x = -7.23329154, y = -5.375957437, z = .4832574136], [x = -.30941167, y = .4572819962, z = .5682422207], [x = -.30941167, y = -.4572819962, z = .5...](images/GroebnerIntro_422.gif)
Finally, 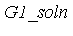 and
and  together represent the 14 solutions of the original polynomial system
together represent the 14 solutions of the original polynomial system 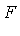 .
.
![[4*x^2+x*y^2-z+1/4, 2*x+z*y^2+1/2, z*x^2-1/2*x-y^2]](images/GroebnerIntro_426.gif)
Check the solutions.
| > |
seq( eval(F, G1_soln[i]), i=1..nops(G1_soln) ); |
![[0, 0, 0], [0, 0, 0]](images/GroebnerIntro_427.gif)
| > |
seq( eval(F, G2_soln[i]), i=1..nops([G2_soln]) ); |
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_428.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_429.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_430.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_431.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_432.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_433.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_434.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_435.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_436.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_437.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_438.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_439.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_440.gif)
![[0.2864e-6, -0.200e-7, 0.6e-7], [0.2864e-6, -0.200e-7, 0.6e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.138e-7, -0.140e-7, 0.104e-7], [0.3238e-6-0.83e-7*I, -0.479e-6-0.6432e-6*I, 0.5537e-6+0.677e-7*I], [0...](images/GroebnerIntro_441.gif)
Concluding Remarks
In addition to reference [1], for further reading on the solution of systems of polynomial equations and related topics, the undergraduate-level textbook [2] is highly recommended.
References
[1] K.O. Geddes, S.R. Czapor and G. Labahn, Algorithms for Computer Algebra , Kluwer Academic Publishers, Boston, 1992.
[2] D. Cox, J. Little and D. O'Shea, Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra , Springer-Verlag, New York, 1992.
![]() , under the assumption that
, under the assumption that ![]() represents the complex number
represents the complex number ![]() . For example,
. For example, ![]()
![]()
![]() with respect to the following side relation which the variable
with respect to the following side relation which the variable ![]() must satisfy:
must satisfy: ![]() .
. ![]() [
[![]() ] over some coefficient domain
] over some coefficient domain ![]() but we really want to represent the expression in a canonical form as an element of the quotient ring
but we really want to represent the expression in a canonical form as an element of the quotient ring ![]() -- i.e. as a polynomial modulo the ideal generated by
-- i.e. as a polynomial modulo the ideal generated by ![]() .
. ![]() ?
? ![]() -- i.e. as a polynomial of degree 1 in the variable
-- i.e. as a polynomial of degree 1 in the variable ![]() .
. ![]() -->
--> ![]() .
. ![]()
![]()
![]() which has the alias
which has the alias ![]() in Maple.
in Maple. ![]()
![]() which represents
which represents ![]() .
. ![]() is:
is: ![]() .
. 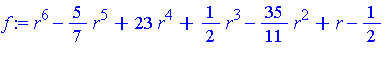
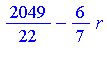
![]() .
. 
![]() and
and ![]() and we wish to simplify the expression with respect to the following side relation:
and we wish to simplify the expression with respect to the following side relation: ![]() .
. ![]() and to represent
and to represent ![]() and
and ![]() in the expression by the symbols
in the expression by the symbols ![]() and
and ![]() , respectively. We are then faced with the problem of simplifying a multivariate polynomial with respect to a multivariate side relation.
, respectively. We are then faced with the problem of simplifying a multivariate polynomial with respect to a multivariate side relation. ![]() [
[![]() ] and we wish to express it (in a canonical form, if possible) as an element of the quotient ring
] and we wish to express it (in a canonical form, if possible) as an element of the quotient ring ![]() .
. ![]() ?
? ![]()
![]()
![]()
![]() [
[![]() ] and one or more side relations
] and one or more side relations ![]() (
(![]() ), is it possible to specify a canonical form for elements of the quotient ring
), is it possible to specify a canonical form for elements of the quotient ring ![]() [
[![]() ] /
] / ![]() where
where ![]() is the ideal generated by the polynomials
is the ideal generated by the polynomials ![]() ?
? ![]() where
where ![]() is a set of one or more side relations. When the simplify command is invoked in this form, Maple applies the theory of Groebner bases. Specifically, a Groebner basis for
is a set of one or more side relations. When the simplify command is invoked in this form, Maple applies the theory of Groebner bases. Specifically, a Groebner basis for ![]() is computed and then
is computed and then ![]() is reduced modulo this Groebner basis by transformations to be described in a subsequent section.
is reduced modulo this Groebner basis by transformations to be described in a subsequent section. ![]() where
where ![]() is a list of variables in the desired order.
is a list of variables in the desired order. ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
. ![]()
![]()
![]()
![]() is equivalent to zero, and therefore its canonical form must be 0 (regardless of ordering).
is equivalent to zero, and therefore its canonical form must be 0 (regardless of ordering). ![]()
![]()

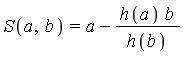 .
. 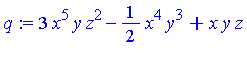
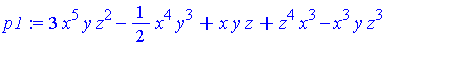
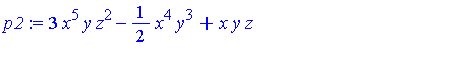
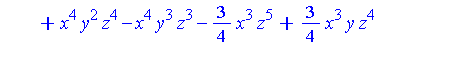
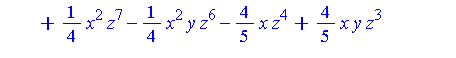
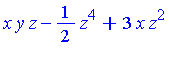

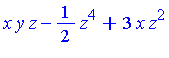
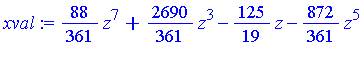
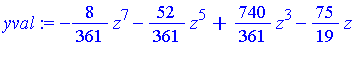
![[4*x^2+x*y^2-z+1/4, 2*x+z*y^2+1/2, z*x^2-1/2*x-y^2]](images/GroebnerIntro_342.gif)
![[[x = -1/2, y = 1/2*2^(1/2), z = 1], [x = -1/2, y = -1/2*2^(1/2), z = 1]]](images/GroebnerIntro_368.gif)
![[[x = -1/2, y = 1/2*2^(1/2), z = 1], [x = -1/2, y = -1/2*2^(1/2), z = 1]]](images/GroebnerIntro_369.gif)
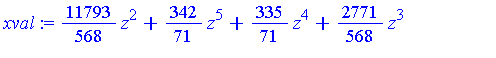


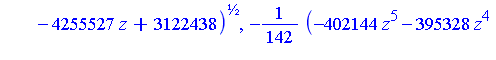

![[4*x^2+x*y^2-z+1/4, 2*x+z*y^2+1/2, z*x^2-1/2*x-y^2]](images/GroebnerIntro_426.gif)