A chiral aperiodic monotile

David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss, 2023

The "hat" aperiodic monotile resolves the question of whether a single shape can force aperiodicity in the plane. However, all tilings by the hat require reflections; that is, they must incorporate both left- and right-handed hats. Mathematically, this leaves open the question of whether a single shape can force aperiodicity using only translations and rotations. (It also complicates the practical application of the hat in some decorative contexts, where extra work would be needed to manufacture both a shape and its reflection.)

In this paper we present a shape that resolves the question above: one that tiles the plane aperiodically without reflections. Specifically, we show that the equilateral polygon referred to in our first paper as Tile(1,1) is a weakly chiral aperiodic monotile: if you simply forbid reflections by fiat then it admits only non-periodic tilings (even though it tiles periodically if you allow reflections). We then modify the edges of Tile(1,1) to produce a family of shapes we call "Spectres", which are strictly chiral aperiodic monotiles: they tile aperiodically using only translations and rotations, even when reflections are permitted.

This page collects the resources associated with this work.

Tools and links

• Our article was published in the journal Combinatorial Theory In September, 2024 (Volume 4, Issue 2). You can read the the article on their site, or visit the (identical) preprint on the arXiv.

• You can create your own patches of Tile(1,1), and save them as PNG files, using an interactive application that runs in your web browser.

• You can download an SVG file containing outlines of three variations of the Spectre if you want to cut out copies and experiment with them.

• Every tiling by Spectres is closely related to a tiling with a sparse distribution of hats lying within a dense field of turtles, and one with a sparse distribution of turtles lying within a dense field of hats. You can watch a short animation that demonstrates this equivalence by morphing continuously between these three tilings. You can also download your own copy (which you can more easily watch looped).

Sample images

Here are some sample images you can use in publications, media, etc. Feel free to modify these images to suit your tastes.

All images, and the MP4 animation above, are licensed under a Creative Commons Attribution 4.0 International License.

A larger version of the banner image above, crossfading between Tile(1,1) and a Spectre with curved edges.
[2000x1138 PNG] [Scalable PDF]

A simpler, zoomed-in patch of Tile(1,1), with "odd" tiles shaded.
[2000x1842 PNG] [Scalable PDF]

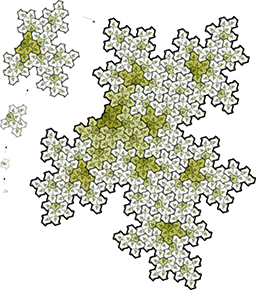
A copy of Figure 2.2 of the paper, showing five generations of the Spectre cluster after applying our substitution rules.
[1767x2000 PNG] [Scalable PDF]

A looping animated GIF showing the same equivalence described above between tilings by Spectres and tilings by combinations of hats and turtles.
[500x500 GIF]

If you would like to contact us about this paper, please email me at csk@uwaterloo.ca.