Metamorphoses and deformations

Escher made repeated use of a family of metamorphosis techniques in his graphic work. Perhaps the most famous example of all of these techniques is his print Metamorphosis II.

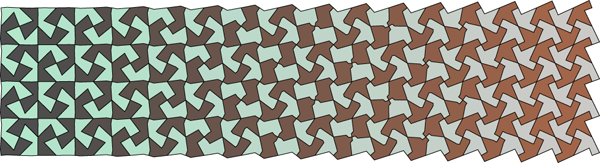
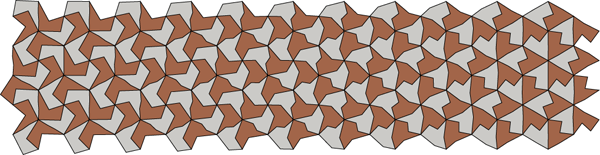
A few decades later, architect William Huff began to assign his students the task of drawing "Parquet Deformations", abstract designs depicting tilings that slowly evolve in space. The results are clearly related to Escher's metamorphoses, though more abstract and mathematical. Parquet Deformations were popularized by Douglas Hofstadter in his Metamagical Themas column in Scientific American, later reprinted in the book of the same name.

I have long been interested in trying to formalize these different styles of metamorphoses and deformations. Even in the relatively simple case of linear interpolation between the shapes of two tilings, a wide range of attractive decorative possibilities arise. I include some sample images below with inadequate explanation. I have also created some related designs inspired by Islamic star patterns; those are shown on the project page for that topic. I discuss the mathematical details of Escher's Sky-and-Water device in my GI 2004 paper on dihedral Escherization. See also my 2008 Bridges paper on the subject.

More recently, I have experimented with a few new curve interpolation schemes for parquet deformations that are not necessarily based on simple linear interpolation, but more attuned to the aesthetic possibilities of parquet deformations. I experimented with a discrete grid-based growth strategy inspired by Huff's designs; curves based on iterated function systems; and organic growth in the style of Pedersen and Singh's labyrinths. The results appear in the Bridges 2010 paper listed below. Click on the images below for a PDF version.

Papers

Curve evolution schemes for parquet deformations. Bridges 2010.
Metamorphosis in Escher's Art. Bridges 2008.
Islamic star patterns from polygons in contact. GI 2005.
Dihedral Escherization. GI 2004.

Other resources

A lovely gentleman named Yusuf X implemented an interactive viewer for an Islamic parquet deformation using the HTML Canvas and Javascript. He's allowed me to post it on his behalf. You can try it here.
Inspired by the "Islamic parquet deformations" mentioned in my PhD thesis and in the GI 2005 paper, mathematical beader Florence Turnour has created a gorgeous beaded parquet deformation. Amazing!

All images are copyright by Craig S. Kaplan. You are free to use them for personal and non-commercial purposes. Please check with me about any other uses.