Long Division Over $\mathbb{R}$ and $\mathbb{Z}_p$ Part $2$

Hello everyone. In this video, I'd like to do one more quick example of long division.

So here we have $5x^2+1$, and I want to know what happens if I divide that into $x^3+3x^2+2x+1$, and I want to do this over $\mathbb{R}$.

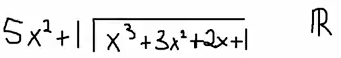
So my first step I need to figure out how many times $5x^2$ goes into $x^3$, that's $1/5x$ times. So if I multiply those two things together I'm going to get $x^3+1/5x$.

When I subtract I get $3x^2+9/5x+1$.

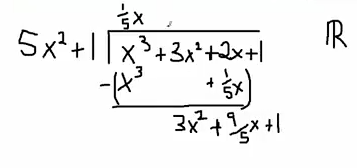
Now lastly I want to know how many times $5x^2$ goes into $3x^2$ that's $3/5$ times. So it’s going to be $3x^2+3/5$. Now I'm going to subtract, and that's going to give me $9/5x+2/5$ as my remainder and $1/5x+3/5$ as my quotient.

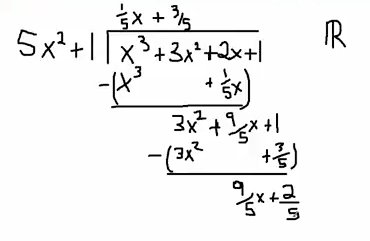
Now why did I do this example? The reason why I did this example is for the following interesting little tidbit here. So this was the operation over $\mathbb{R}$. In a previous video I made, the division worked out over $\mathbb{R}$ and if I just reduced the quotient and the remainder over $\mathbb{Z}_5$, everything worked out.

But here there's a huge problem, and the huge problem is that well I'm dividing by $5$ a lot, which I can't do in $\mathbb{Z}_5$ because $5\equiv 0 \bmod 5$.

So here you'd have to actually redo the computation. It's not enough to do the computation over $\mathbb{R}$ and just reduce, but here the computation over $\mathbb{Z}_5$ is easy because $5x^2\equiv 0 \bmod 5$, so this is just dividing $x^3+3x^2+2x+1$ by the polynomial given by $1$, and so there is no remainder, and the quotient is just the original polynomial.

So something to keep in mind that you can't always just reduce the quotient and remainder. If you have integers and you do the computations over $\mathbb{R}$, there's some chance that you could reduce them, but it's not a given rule of thumb, okay? You have to be a little bit careful about this fact.

Okay, that's all I want to say in this video. Hopefully it helped clarify a couple of points that at least my class had in class. Thank you very much.