Loading [MathJax]/jax/element/mml/optable/BasicLatin.js

Long Division over $\mathbb{R}$ and $\mathbb{Z}_p$

Hello everyone. In this video, we're going to talk about long division, and we're going to do it over a couple of different fields.

Question: What are the quotient and remainder when $x^5+3x^4+2x^2+4x+1$ is divided by $x^2-2x$ over $\mathbb{R}$? How about over $\mathbb{Z}_5$?

Solution Over $\mathbb{R}$

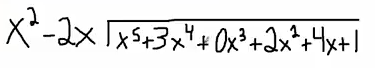
We'd like to long divide these two polynomials. As you've noticed here in the middle, I have this extra $x^3$ with a $0$ coefficient. It's just a placeholder to help me keep everything organized as I attempt to go through this.

Okay, so let's begin. The question that I want to know is what number do I have to multiply $x^2$ by to get to $x^5$ over $\mathbb{R}$? $x^3$. Now I take $x^3$, multiply it by this whole polynomial $x^2-2x$, what do I get?

I'm going to get $x^5$. If these don't match up, then you've made a mistake on the first step, and I'm going to get $-2x^4$.

Now I subtract, and that's going to give me $5x^4$. Now I'm going to bring down the $0$ term, again it's not important that you write this. I'm just doing it for organizational purposes.

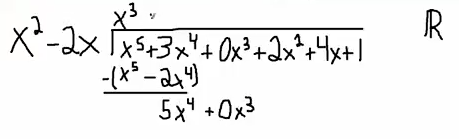
Now the number I'm going to multiply to $x^2$ to get to $5x^4$ that's $5x^2$, and then I'm going to take $5x^2$ multiply by the $-2x$, that’s going to be $-10x^3$.

Now we subtract. First two terms cancel again. Next two terms, it's going to give me a $10x^3$. plus, let's bring down the next term, $2x^2$.

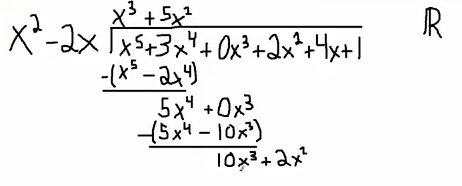
$x^2$ multiplied by $10x$ is $10x^3$, so up top I go $10x$. By the way, another way to see this, doesn't always work - well it does always work we have to think of the word divide carefully, you could divide $10x^3$ by $x^2$, and that will give you the number on the top. You have to divide properly in whatever field you're working in. In this case, it's $\mathbb{R}$, so we have a good understanding of what's going on.

$10x^3$ and $-20x^2$. Subtract, so it's going to be $22x^2$, then I'm going to drop down the $4x$

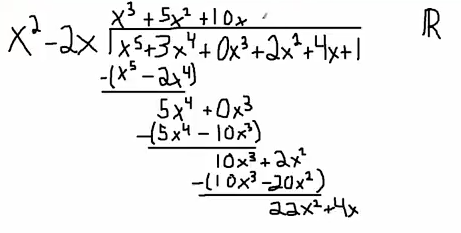
I'm going to do the long division so $x^2$ goes into $22x^2$ $22$ times. So I'm going to get $22x^2-44x$. And my last subtraction is going to give me $48x+1$. And remember that this is the remainder, the $48x+1$, and up top is my quotient.

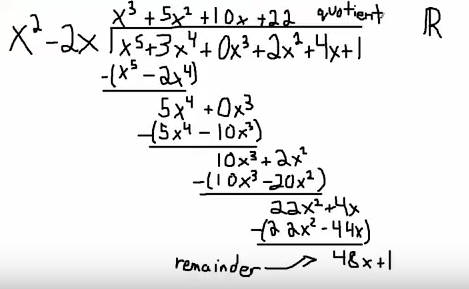
Solution Over $\mathbb{Z}_5$

Okay, great. So there's a long division example over $\mathbb{R}$. Now what I'd like to do is I'd like to do the same computation over $\mathbb{Z}_5$ and see what changes, okay?

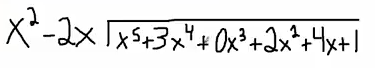
So again $x^2$ goes into $x^5$, $x^3$ times. So now, what are we going to get? We're going to get $x^5-2x^4$, and $3x^4-(2x^4)=5x^4\equiv 0$ in $\mathbb{Z}_5$. So bring down the $0$, that doesn't work, let's go down to the next term, which is going to be $2x^2+4x$.

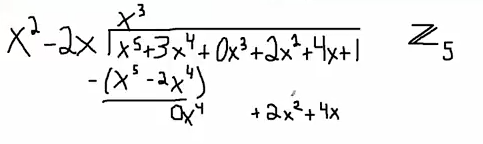
Now the question is what do I have to multiply $x^2$ by to get to $2x^2$, that's easy, it's going to be $2$. So that's going to give me $2x^2-4x$. $4-(-4)=8$, that's going to leave me with a remainder of $3x+1$. And that is it.

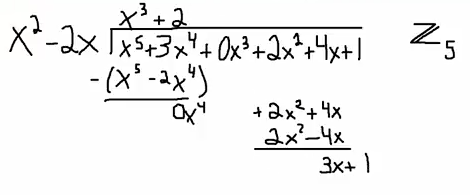
So here's my remainder, it’s now $3x+1$, and my quotient here is $x^3+1$. So if we go back to the previous example, the remainder was $48x+1$ and our quotient was $x^3+5x^2+10x+22$, but if you reduce this $\bmod 5$, we actually get the same answer.

If you reduce $48x+1\bmod 5$, you get $3x+1$ and our second remainder is $3x+1$. It also works for the two quotients.

So, in this setting, you do get the same answer if you just reduce the work over $\mathbb{R}$, over $\mathbb{Z}_5$. It's something to think about. Does it always happen? I'll probably make another video where it may or may not happen. I'm going to try a different one. But that's the idea, okay? So hopefully this gives you a little bit of practice with long division and thank you very much.