Polar Coordinates

Hello everyone. In this video, we are going to convert a complex number in standard form into polar coordinates.

Using the fact that $\tan(\pi/12)=2-\sqrt{3}$, find the polar coordinates of

$$-\sqrt{3}-(2\sqrt{3}-3)i$$

Solution

So the solution, in order to do this, we need to compute two facts, right? We need to compute the angle with respect to the $x$-axis, and we need to compute the length of our vector, the radius, or the modulus of this complex number. So that's what we're going to do first.

So it's usually easier to compute the length of your complex number, so we're going to begin with that. So how do we do that? Well we're going to just take the modulus, and we're going to set this to equal $r$, okay, $r$ for radius.

$$\begin{align*} r&=|-\sqrt{3}-(2\sqrt{3}-3)i|\\ &=\sqrt{(-\sqrt{3})^2+(-(2\sqrt{3}-3))^2}\\ &=\sqrt{3+4(3)-12\sqrt{3}+9}\\ &=\sqrt{24-12\sqrt{3}}\\ &=2\sqrt{6-3\sqrt{3}} \end{align*}$$

Now it's always good to do a little bit of a sanity check. $\sqrt{3}< 2$ so $6-3\sqrt{3}$ is positive so we didn't make any obvious blunders. So that's going to be the radius of our complex number up here.

Now we want to compute the angle, and so hopefully we're going to need this fact that $\tan(\pi/12)=2-\sqrt{3}$. I made this problem, so there's some chance that there's a mistake, but I'm hoping that this is going to work out, we need this fact that we're given, okay?

So now with the radius, what I'm going to do is I'm going to try to compute the $\theta$ value, the angle with respect to the $x$-axis. So now, to compute $\theta$, the angle of rotation with respect to the $x$-axis, we perform

$$\begin{align*} \arctan\left(\frac{y}{x}\right)&=\arctan\left(\frac{-(2\sqrt{3}-3)}{-\sqrt{3}}\right)\\ &=\arctan\left(\frac{\sqrt{3}(2-\sqrt{3})}{\sqrt{3}}\right)\\ &=\arctan(2\sqrt{3})\\ &=\pi/12 \end{align*}$$

Now you have to be a little bit careful at this point. We can't immediately jump the gun and conclude that our angle is $\pi/12$, we have to do one last check. What is that last check? Well if I take $\tan(\pi/12)$, where does this send me?

If I think about this in the complex plane, this sends me into quadrant $1$, okay? Now quadrant $1$, now it's fine, maybe the answer is in quadrant $1$, but if we look at the actual number here, the original complex number has a negative $x$ value and a negative $y$ value.

So if we think about this in the complex plane, the number lives somewhere in the bottom left quadrant, or quadrant $3$. But $\pi/12$, the angle $\pi/12$, is somewhere in the first quadrant.

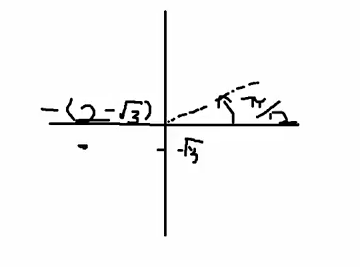
So what's the problem? Did we break math? I mean, we did say that $arctan\left(\frac{y}{x}\right)$ should be equal to the angle that we get in polar coordinates when we convert.

The problem here is that $\arctan$ has a range between $-\pi/2$ and $\pi/2$. It's the easiest way to say this.

So what does that mean? $\arctan$ is kind of a silly function, right? It doesn't determine which $\theta$ you want, and why does it not do that? Well the main reason is that $\tan$ is $\pi$ periodic. So because $\tan$ is $\pi$ periodic, we're going to have this issue that we either want the point you get when you simplify, or the point where we add an extra copy of $\pi$, and the functions don't know this.

So $\arctan$ doesn't know that I wanted the one in the third quadrant, not one in the first quadrant.

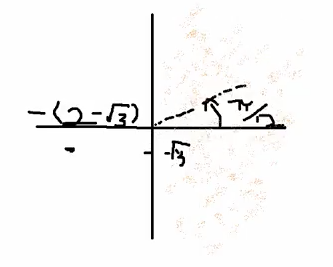
$\arctan$ always returns points in the region defined by the highlighted region shown above. So $\arctan$ only knows angles between $-\pi/2$ and $\pi/2$. That’s going to be all this stuff shaded in orange, okay?

So in order to get the point on the other side, you have to think do I have to add an extra copy of $\pi$ or not? Also note that the imaginary axis, $\arctan$ has a lot of problems with because infinities and things like this, right? $\arctan$ doesn't ever equal a value between exactly $-\pi/2$ and $\pi/2$. So for those values, you just have to sort of look at them and make sure you know which one is which, right?

It's very easy to tell when a complex number is on the complex axis, that's not hard, so you don't need to go through all this rigmarole if you're dealing something like that.

Okay, with that being said, we know now that our $\theta\neq\pi/12$, but $\theta=\pi+\pi/12=13\pi/12$. Hence, in polar coordinates our number is

$$\begin{align*} -\sqrt{3}-(2\sqrt{3}-3)i&=re^{i\theta}\\ &=r(\cos(\theta)+i\sin(\theta))\\ &=2\sqrt{6-3\sqrt{3}}(\cos(13\pi/12)+i\sin(13\pi/12)) \end{align*}$$

So in polar coordinates, we get this messy looking expression, but nonetheless it's in that expression.

The important message to take away from this exercise is the following: even when you do $\arctan\left(\frac{y}{x}\right)$, you're not guaranteed to get the correct answer. You need to double check your final answer, and make sure that the angle that you get is actually the angle that you want.

Again, I like my angles between $0$ and $2\pi$, so I always try to put my angles between $0$ and $2\pi$, it's up to you. If you've got a negative number, that's fine, just make sure that you get the correct negative angle, okay, and that you're not off by a $\pi$ factor.

So, great. I hope this gives you a little bit of insight as to converting and some of the pitfalls, and that's all I have to say. Thank you very much for listening and good luck.