RSA

Hello everyone. In this video, we're going to talk about RSA. Now here, again, I'm using Sage Math Cloud as my LaTeX editor, but here I'm actually using the Sage version of it. So I can actually have access to Python and Sage and all of the mathematical commands, which I'll use to do some of the computations in this video.

So in order to do RSA, let's talk about the framework again.

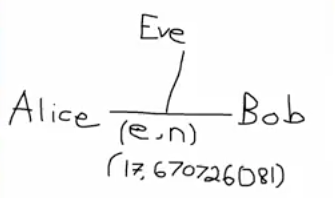
So we're going to have our Alice, and we're going to have Bob, and we're going to put Eve in the middle. Eve for eavesdropper. Some people use Oscar I'm going to use Eve.

So the idea is that Alice and Bob want to share messages. Bob wants to send a message to Alice, okay, but now Bob can't just send a message across the unsecured stream, or unsecured line, think of this as like the internet because then Eve can read it and see it. So Bob needs to encrypt it somehow, so that when Eve sees the encrypted message, she won't know what's going on, but Alice somehow knows how to decrypt it.

Finding Public Key

So Bob wants to send Alice a message, and Bob wants to send Alice a secure message using RSA. So what's going to happen? So Alice is going to do what? Alice is going to, in the RSA scheme, she's going to choose a public key, $(e,n)$, satisfying $n=pq$. What do we have to have about $e$? $e$ is a positive integer satisfying $\gcd(e,(p-1)(q-1))=1$.

$(p-1)(q-1)$ is also known as $\phi(n)$.

So Alice, Eve, and Bob, so everyone's going to have this public key. This public key is going to be given by $(e,n)$. Everyone knows the public key $(e,n)$. I know it, you know it, Eve knows it, grandma knows it, everyone knows it.

So what do we do this? Okay, so here's the situation. Let's actually pick some examples of $n$, $p$, and $q$.

So what am I going to pick? I'm going to pick $p=$next_prime$(12345)$. This command next_prime is in Sage Math Cloud and I'm using it because I want an actual large prime. So I'm going to pick the first prime after $12345$. $q=$next_prime$(54321)$.

Again remember these are all Sage commands, next_prime and everything, if you know Python, it's kind of like Python with a little bit more to it. If not, that's okay. Hopefully this is still pretty reasonable.

So next_prime will set $p$ to be the next prime after $12345$, and $q$ will be the next prime after $54321$. $n=pq$, and we need to pick an integer $e$, so, I don’t know, I'm going to pick $e=17$.

So p is the value $12347$, okay, and $q$ is the value $54323$, apparently those two numbers are prime, so that's great.

$n=pq=670726081$, so something along lines of $670$ million-ish. Okay so it's a pretty big number, and $e=17$, and $\gcd(e,(p-1)(q-1))=1$.

So with this, I guess I mean I've already done it on the picture but maybe I should mention here. Alice publishes $(e,n)$. So notice that $(e,n)$ is what's published, it's not $p$ and $q$, it's the product, it's just the product, whatever number this is.

So in our example, we're going to publish $(17,670726081)$. So that's what's being published.

Encrypting Message

Now Bob wants to send a message. So what’s Bob's message? So let's talk about Bob now. Bob wants to send his message, $M$, an integer strictly between $1$ and $n$.

So what's Bob going to do? Well Bob's going to encrypt $M$. How is Bob going to encrypt M? Bob computes $C\equiv M^e\bmod n$. And we want $0 < C < n$.

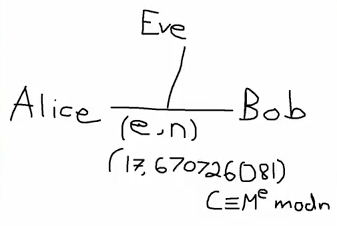
Alright, so we've added this to our picture and we're going to try to send $C$ over in a minute, but first let's actually take an example.

So here we're going to take $M=11111111$. For whatever reason he likes this number and he's going to send it. $C$ we're going to compute to be $M^e\bmod n$ so we can do that with this command called power_mod.

So what will this do? This will produce $M^e\bmod n$. It's sort of intuitive. Great, so $C$ is this number $512017456$, so $512$ ish million.

Okay, so Bob's computed this, now Bob's going to send $C$ to Alice.

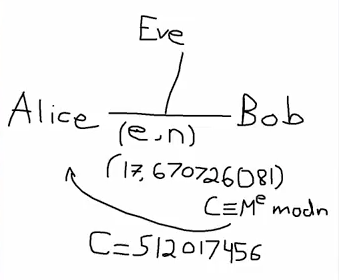
So again notice that Eve gets to see $C$. So Eve doesn't know what $M$ is, but Eve gets to see $C$, and she gets to see $e$ and $n$. Notice that from this weird number $512017456$, it's not immediately obvious that the message was $11111111$.

So now Alice has $C$, but Alice knows a couple other things, right? She knows $p$ and $q$, she knows $e$. These are part of her private keys.

Decrypting Message

So what's Alice going to do now? Alice receives $C$ and computes $d$ such that $ed\equiv 1 \bmod{(p-1)(q-1)}$. We'll see why this $d$ is important in a minute. $d$ is going to be $e^{-1}\bmod{(p-1)(q-1)}$.

By the way, sanity check, right? Why does this exist? This exists because $\gcd(e,(p-1)(q-1))=1$.

$d$ happens to be $118351661$, after solving for it in Sage. So in our picture, Alice has this private key, $d$, and again in our example it's $118351661$. Now what's Alice going to do? Well Alice is going to compute $R\equiv C^d\bmod n$.

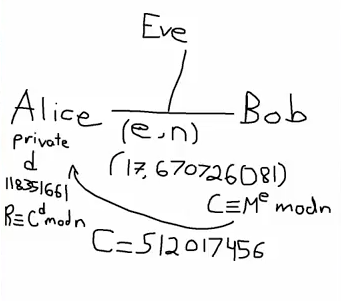
Okay now is a good time to ask yourself, “What value is the computer going to print out for $R$?” So if you understand everything, you should know exactly what's going to happen here. So take a minute, think about it, and then come back.

What should the the answer be? The answer should be $M$, so $11111111$. So this $R$ that you compute when you compute $C^d$ is going to be the original message. So Eve is going to have a very difficult time figuring out what the original message is. She has to solve some sort of discrete log problem, or she has to try to figure out what $d$ is. Either way, it's going to be tricky.

Given this $512017456$, it's tough to know that it came from: $11111111$, right? It's not easy to solve the problem. If you could take logarithms, this would be easy to do, but you can't do that with congruences. It's not that obvious because of the periodicity properties.

This $\gcd(e,(p-1)(q-1))=1$, that's important in the proof, right? The reason why this $R$ works out is because $\gcd(e,(p-1)(q-1))=1$, $p$ and $q$ are co-prime, you use a combination of Chinese Remainder Theorem and Fermat's Little Theorem to get this going. And that's that.

So by the way, all these computations took like instantly on Sage, right, and it didn't matter what numbers I used, right? I mean like if I changed 17 to next_prime$(12345678)$, so $12345701$.

So now if we run these computations, so $M^e$, it still spits out the answer very quick. That happened instantly even though the number was some huge $8$ digit number, it's still computed $M^e\bmod n$ in a second.

It also computes $ed\equiv 1 \bmod{(p-1)(q-1)}$ instantly, okay? So this inverse is really quick to compute. How do we compute the inverse quickly? The Extended Euclidean Algorithm. I don't actually know what's going on. You can actually look what's going on under the hood in Sage, but I presume that's what's happening, some sort of nice algorithm like that.

So you can change the $e$ to make it more complicated or simpler it doesn't matter. The math is still going to work out.

We talked a little bit in class about which $e$’s to use. You probably want to use something bigger than $17$. You probably want something so that $2^e>n$, just so that you can't take $n$th roots of the message that would be kind of silly. So you actually want to do a reduction is what I'm saying, but that's it. That's RSA.

So hopefully this gives you an idea of how to use RSA effectively, and how you can go about sending messages using RSA. This is basically the entire encryption scheme. The only thing that's missing is the proof that $R=M$, but hopefully the example gives you a little bit of an insight as to why that might be the case. Alright thank you very much for your time, hope this helped.