Fall 2000 Exam Question 7

Hello everyone. In this video, we continue our voyage through the Fall 2000 exam, and now we've reached question $7$.

Question Part $1$: State the Rational Roots Theorem.

Solution to Part $1$

First part’s actually not too, too bad. Now of course, on our exam, we won't have this issue because we'll be given all the theorems, but let's state it anyways.

Theorem (RRT): Let $f(x)=a_nx^n+...+a_1x+a_0\in\mathbb{Z}[x]$. If $r=\frac{a}{b}$ is a rational root of $f(x)$, then $a\mid a_0$ and $b\mid a_n$.

So clearly this is going to be a question about the Rational Roots Theorem based on the first part.

Question Part $2$: Let $f(x)=4x^4+8x^3+9x^2+5x+1$. Determine the rational roots of $f(x)$.

Solution to Part $2$

So by the previous theorem we know that the only possibilities are when a divisor of $1$ is in the numerator, and a divisor of $4$ is in the denominator. This gives us 6 possibilities: $\pm 1,\pm 1/2, \pm 1/4$.

Now in order to save time, and as you can see this question is very lengthy, I'm just going to plug them in and go with it.

$$\begin{align*} f(1)&=27\\ f(-1)&=1\\ f(1/2)&=7\\ f(-1/2)&=0\\ f(1/4)&=189/64\\ f(-1/4)&=13/64 \end{align*}$$

Only one of these is $0$, that's the most important part, $f(-1/2)$, so $-1/2$ is the only rational root of $f(x)$.

Question Part $3$: Factor $f(x)=4x^4+8x^3+9x^2+5x+1$ over $\mathbb{Q}[x],\mathbb{R}[x],\mathbb{C}[x]$, and $\mathbb{Z}_5[x]$.

Solution to Part $3$

So clearly we want to use the fact that we have a rational root, namely $-1/2$. So by the Factor Theorem, we know that if $-1/2$ is a rational root, $2x+1$ must be a factor. So if we know a factor, we can just divide out by using long division, and get our other factor. So let's do our long division, here I've done it in some paint program.

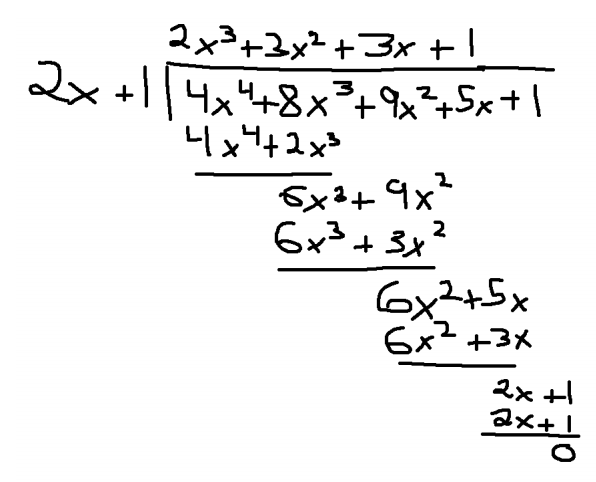
So $2x+1$ goes into $4x^4+8x^3+9x^2+5x+1$. How do we do this? Well compare leading coefficients, so $2x$ into $4x^4$, that's $2x^3$. So we do the division, and what do we get? So we multiply $2x+1$ by $2x^3$, that gives us $4x^4+2x^3$.

Subtract we get $6x^3$. Drop down the other term, $9x^2$. $2x$ goes into $6x^3$ $3x^2$ times. Write it down. Okay then simplify, so $9x-3x=6x$, drop down the $5$.

$2x$ goes into $6x^2$ $3x$ times. $6x^2+3x$, multiply that through, we're going to get $2x+1$, that's good, we want a remainder $0$.

Now when we do this though we should keep note of something, right? So we do this and we have that $f(x)=(2x+1)(2x^3+3x^2+3x+1)$, that's the Division Algorithm.

Now I've always said that the goal of these types of factoring questions is to get down to a quadratic. When you get down to a quadratic, you know what to do. We unfortunately still have a cubic, so if we have a cubic and we still need to factor it, well we really don't have too many tricks, right?

They didn't give us a factor in this question, so we're left with only one option and our one option to attempt to factor this, and pray to God this is going to work, is that this thing has another factor that's rational, but we already saw that there's only one possibility for a rational factor, and that's $-1/2$. So $-1/2$ might be a repeated root, that's our only hope at this point. Let's give it a shot and plug $-1/2$ into this cubic.

$$2(-1/2)^3+3(-1/2)^2+3(-1/2)+1=-2/8+3/4-3/2+1=2/4-3/2+1=0$$

$2x+1$ is a repeated factor of $f(x)$. So let's do another long division.

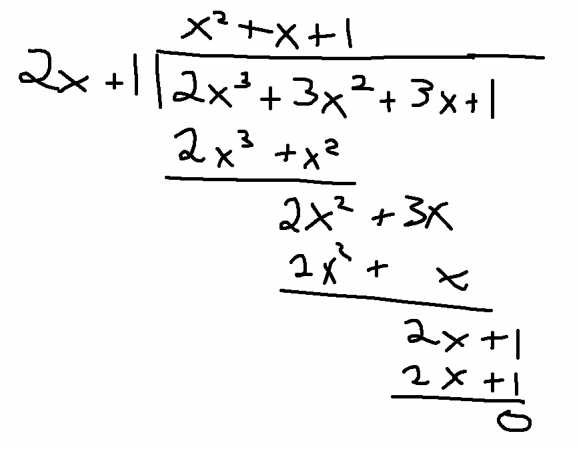
So if we do our long division, $2x$ into $2x^3$ is $x^2$, simplify we get $2x^2+3x$. Again $x\cdot 2x=2x^2$. Do that, simplify, again we get $0$.

So now our factorization is $f(x)=(2x+1)^2(x^2+x+1)$.

It should be noted if I expand this out, this is going to also work over $\mathbb{Z}_5$, which is another field that we have to work over so keep in mind this factorization is good over all four of those rings.

So the roots of $x^2+x+1$ are given by the quadratic formula, right, I mean, so now we have a quadratic, we know what to do.

$$x=\frac{-1\pm\sqrt{1^2-4(1)(1)}}{2}=\frac{-1\pm\sqrt{3}i}{2}$$

These factors are imaginary, so we know we have the complete factorization over $\mathbb{Q}$ and the complete factorization over $\mathbb{R}$, it's given by $f(x)=(2x+1)^2(x^2+x+1)$.

To get the factorization over $\mathbb{C}$, well $\frac{-1\pm\sqrt{3}i}{2}$ are our two roots so just split them up and write them as factors.

$$f(x)=(2x+1)^2(x+(1+\sqrt{3}i)/2)(x+(1-\sqrt{3}i)/2)$$

So now over $\mathbb{Z}_5$, we have to do one little check, right? So now we have a quadratic polynomial and we want to know if it's irreducible over $\mathbb{Z}_5$. Well from the last homework question, the last homework of this course, question $7$, tells us that if this thing factors, it must have a root, right? If it's going to factor as something, it's got to factor as a linear term times a linear term to get to a quadratic term. So if there's a linear factor, then it must have a root in $\mathbb{Z}_5$. So just check the five numbers and see if it has a root.

$$\begin{align*} 0^2+0+1&=1\\ 1^2+1+1&=3\\ 2^2+2+1&=2\\ 3^2+3+1&=3\\ 4^2+4+1&=1 \end{align*}$$

We clearly don't get $0$ in any case, and we're done. So thus this has no roots, and hence the factorization over $\mathbb{Z}_5$ is the same over $\mathbb{Q}$ and as over $\mathbb{R}$.

Pretty crazy question, there's a ton of work that went to this question. It's a tougher question, it’s a longer question, there’s a lot of parts, but that's okay.

Again, keep at it, don't give up, and you have to notice a couple of things to hit the Graceland, you know, to get there, but it can be done, okay, that's the kind of the point that I'm making. Again, trickier question, a little harder than the previous ones, but it can still be done.

It helps to read questions beforehand it's sort of a good tip in any exam. Reading questions beforehand definitely helps and I hope that this video helps solve this problem, give you a little bit of insight as what to do when you're trying to factor things. Good luck.