Fall 2000 Exam Question 6

Hello everyone. In this equation, I'm going to do some complex numbers. So I should warn you that I didn't actually double check my answer, but I'm pretty sure it's correct. I'll leave it up to you guys to double check my work, and if I'm wrong let me know, and I'll reproduce the video.

Question: Determine all complex numbers (in polar or standard form) of the equation

$$z^6+2iz^3-4=0$$

Solution

So I'm going to do this in probably polar form by the end, but I'll probably start in standard form. So when I look at this equation, I do see immediately a quadratic, right? $z^6+2iz^3-4$. This is basically a quadratic if I replace $z^3$ with a $w$, so I'm going to that.

Let $w=z^3$ so that $w^2+2iw-4=0$.

By the way, it should be noted that you should try to factor this first, and I tried to factor it and I didn't find the factors by hand. So when you don't find the factors by hand, you can use the quadratic formula to get them. So let's plug it into the quadratic formula.

$$w=\frac{-2i\pm\sqrt{(2i)^2-4(1)(-4)}}{2(1)}=\frac{-2i\pm\sqrt{12}}{2}=\frac{-2i\pm 2\sqrt{3}}{2}=-1\pm\sqrt{3}$$

Now with this, I'm going to take this and I'm going to try to solve the final equation. So now I have $w=-1\pm\sqrt{3}$, and $w=z^3$, so now it suffices to solve $z^3=-i-\sqrt{3}$ and $z^3=-i+\sqrt{3}$.

So we should right now immediately be thinking oh I should be using CNRT. I have a cubic thing is equal to some complex number, so I should be able to take cube roots by converting to polar form and transferring.

So I'm going to take our two equations and I'm going to do the switcheroo that I did in class, right? So the way I like to convert these is by taking out the modulus, right, because I need to write this as $r$ times something with norm $1$, okay?

So compute the modulus, so compute the length of these two vectors. $|-i\pm\sqrt{3}|=\sqrt{(-1)^2+\sqrt{3}^2}=2$. It doesn't matter if I use $+\sqrt{3}$ or $-\sqrt{3}$ because I square the term inside the square root. So $\pm\sqrt{3}^2$ is going to be the same.

Thus we're solving these two equations given by

$$z^3=2\left(\frac{\pm\sqrt{3}}{2}-\frac{i}{2}\right)$$

Now this should look like some sort of nice trig identity, and in fact it is. So again, there's no shame, draw the little picture, and figure out what angle this should be.

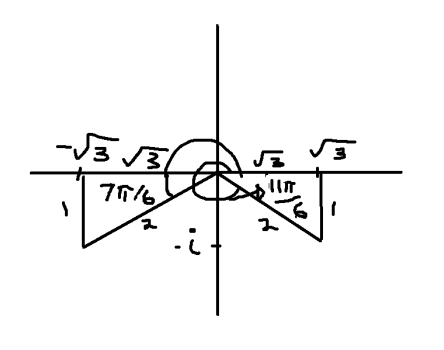
So $-\sqrt{3}/2-i/2$. So $\cos$ and $\sin$ are negatives that happens in the third quadrant. $\cos$ is $\sqrt{3}/2$, so my adjacent should be $\sqrt{3}$, and my hypotenuse should be $2$. So that gives me the triangle in the third quadrant, and that angle is $7\pi/6$. Remember shortest angle goes with the shortest side.

Similarly for $\sqrt{3}/2-i/2$. So $\cos$ is positive and $\sin$ is negative, that's quadrant $4$. The angle going to be $2\pi-\pi/6=11\pi/6$.

So now we have the two equations given by $z^3=2cis(7\pi/6)$ or $z^3=2(\cos(7\pi/6)+i\sin(7\pi/6))$, and $z^3=2(\cos(11\pi/6)+i\sin(11\pi/6))$.

So some point of confusion is a lot of people think oh well I had a negatives in the original equation where did the negatives go? Remember that $\sin(11\pi/6)$ is negative, and $\sin(7\pi/6)$ is negative, and $\cos(7\pi/6)$ is negative. So the signs are taken care of by the trig functions.

So thus, now all I have to do is just plug in CNRT. So what does CNRT say? Okay so it says take the cube root of the modulus, and then divide these two angles by $3$, and then add multiples of $2\pi$, and that gives you all of them.

$$\begin{align*} z&=\sqrt[3]{2}\left(\cos\left(\frac{7\pi/6}{3}\right)+i\sin\left(\frac{7\pi/6}{3}\right)\right)\\ z&=\sqrt[3]{2}\left(\cos\left(\frac{7\pi/6+2\pi}{3}\right)+i\sin\left(\frac{7\pi/6+2\pi}{3}\right)\right)\\ z&=\sqrt[3]{2}\left(\cos\left(\frac{7\pi/6+4\pi}{3}\right)+i\sin\left(\frac{7\pi/6+4\pi}{3}\right)\right)\\ z&=\sqrt[3]{2}\left(\cos\left(\frac{11\pi/6}{3}\right)+i\sin\left(\frac{11\pi/6}{3}\right)\right)\\ z&=\sqrt[3]{2}\left(\cos\left(\frac{11\pi/6+2\pi}{3}\right)+i\sin\left(\frac{11\pi/6+2\pi}{3}\right)\right)\\ z&=\sqrt[3]{2}\left(\cos\left(\frac{11\pi/6+4\pi}{3}\right)+i\sin\left(\frac{11\pi/6+4\pi}{3}\right)\right) \end{align*}$$

Now you could simplify this a little bit I chose not to just to show the form, but again this is just a quick application now of CNRT. So once you get it into this nice form, CNRT can take you home.

So hopefully that gave you a little bit of an idea of what's going on. So again make sure you understand how to use CNRT. So once you write it in polar form, divide the angles by the degree, and take the $n$th root of the $r$ value, and just write down your solutions.

Now the question said I can put it in polar or standard form, so I'm going to put it in polar form. I think that’s perfectly reasonable, and it seemed to fall out naturally for me from that form. Okay great. So thank you very much for your time. Hopefully this video was a little bit informative, help you review some complex numbers.