CCC Week 9 Part 2

Introduction

Hello everyone. Welcome to Week 9 part 2 of Carmen's Core Concepts, my name is Carmen Bruni, and in this video series, we talk about the weekly concepts in Math 135. So part 1 of Week 9, that was RSA. In part 2, we're going to talk about complex numbers.

Table of Contents

This week we talked about complex numbers. We'll talk about why it's a field. So if you don't know what the word “field” means, I suggest checking out I believe Week 7 part 2. We talked about rings and fields there. The complex numbers are an example of a ring and also of a field, something we will mention.

We talked about a couple of operations: complex conjugation, properties of modulus. We talked about polar coordinates, and we'll talk about converting from standard to polar form and from polar to standard form. Actually we'll talk about polar to standard form next week I think.

Complex Numbers

So what is a complex number?

Definition: A complex number (in standard form) is an expression of the form $x+yi$ where $x,y \in \mathbb{R}$ and $i$ is the imaginary unit. Denote the set of complex numbers by

$$\mathbb{C}:=\{x+yi:x,y\in\mathbb{R}\}$$

So $i$ on its own has no meaning. $i$ is just an object, okay?

Examples

Some examples are $1+2i, 3i, \sqrt{13}+\pi i, 2$ (which is $2+0i$). So something to think about is that the real numbers are contained inside the complex numbers, so are the rational numbers, so are the integers and so on and so forth.

So a lot of people when they first see complex numbers, they define $i=\sqrt{-1}$. I'm not going to do this and there's a lot of good reasons why we shouldn't be doing this, and one of the reasons is that, that doesn't really make sense, right? I mean when we say like $\sqrt{4}$, what we mean is the positive number such that when I multiply it by itself I get $4$.

But I don't want to define $i$ like that because it's not a positive number, it's an object, okay? So if all I'm doing is saying that $i$ is some object, then what am I going to do with it? Well we'll see.

At the moment, right now, $\mathbb{C}$ is just a set of things, the $+$ in $x+yi$ has no meaning as of now, okay, it's just really a symbol. It's denoted by $x$ with the $+$ symbol and then $yi$.

Now what we're going to do is we're going to give $+$ some meaning, and we're going to give multiplication some meaning. So we're going to turn the complex numbers into a ring. One last note:

Definition: Two complex number $z=x+yi$ and $w=u+vi$ are equal if and only if $x=u$ and $y=v$

$\mathbb{C}$ is a Field

Let's turn $\mathbb{C}$ into a ring and a field, okay? So we turn $\mathbb{C}$ into a commutative ring by defining an addition and actually a subtraction operation, and how do we do this?

We turn $\mathbb{C}$ into a commutatve ring by defining

1. $(x+yi) \pm (u+vi):=(x \pm u) + (y \pm v)i$
2. $(x+yi)(u+vi):=(xu-vy)+(xv+uy)i$

Notice that this also defines the additive inverse, right? So we have the addition structure, and the multiplication structure. That is the structure that we are giving our set $\mathbb{C}$, and this will make it a commutative ring.

Something to note now, this multiplication operation above, well if we had $(0+i)(0+i)$:

$$i^2=i \cdot i=(0+i)(0+i)=((0)(0)-(1)(1))+((0)(1)+(1)(0))=-1$$

So this object that we defined with these two addition and multiplication operations, tell us that this new object, $i$, has the property that $i^2=-1$.

So something to note is now that we have solutions to the polynomial, let's say, $x^2+1=0$ over $\mathbb{C}$. The solution is $\pm i$. So something to think about.

One of the motivations is to try to give algebraic expressions roots. So to try to give all algebraic expression solutions, and we'll see this in the upcoming weeks why we this actually does this.

Now that we know that $i^2=-1$, we can actually remember this operation here, the multiplication operation, just by multiplying it out how we would before.

$$\begin{align*} (x+yi)(u+vi)&=xu+svi+yiu+yivi\\\\ &=xu+(xv+yu)i+yvi^2\\\\ &=(xu-yv)+(xv+uy)i \end{align*}$$

So here we see that multiplication is actually something that we know here, and addition is not too hard either. It’s basically common factoring the $i$. So addition and multiplication are actually very natural operations here.

We note that $\mathbb{C}$ is a field, so how do we note that it's a field? So we know that the inverse of any non-zero complex number, $x+yi$, is actually defined as:

$$(x+yi)^{-1}=\frac{x}{x^2+y^2}-\frac{y}{x^2+y^2}i$$

If you multiply this by $x+yi$, you will see that the answer is $1$. I will leave that as an exercise though for you to check out.

This is the hard way to think about the inverse. We'll learn in a bit that we can look at inverses using an operation called the modulus of a complex number, and that will help us to remember the inverse formula here. But for now, I'm just going to state it and I'll leave it as an exercise for you to check, that if I multiply by $x+yi$ I get $1$.

Complex Conjugation

Complex conjugation, this is a very useful operation but, I mean, if you just look at it, it seems very simple.

Definition: The complex conjugate of a complex number $z=x+yi$ is $\bar{z}:=x-yi$.

So we just negate the imaginary component. So if you think about this graphically, if you have a complex number in the real-imaginary plane, the complex conjugate is just its reflection about the line $y=x$.

Properties of Conjugates (PCJ)

Properties of Conjugates, these are very easy to prove so I'm only going to prove a couple here. They're not hard, one way to do this is to just introduce coordinates, so write $z$ as $x+yi$, write $w$ as $u+vi$ and then just go through the operations.

Proposition (PCJ): Let $z,w \in \mathbb{C}$. Then

1. $\overline{z+w}=\bar{z}+\bar{w}$
2. $\overline{zw}=\bar{z}\cdot\bar{w}$
3. $\bar{\bar{z}}=z$
4. $z+\bar{z}=2\Re(z)$
5. $z-\bar{z}=2i\Im(z)$

So again, all these can be done with just introducing coordinates.

Proof

So here's an example of $3$, for example:

$$\bar{\bar{z}}=\overline{\overline{x+yi}}=\overline{x-yi}=x+yi=z \quad \blacksquare$$

This is the proof of $4$

$$z+\bar{z}=x+yi+x-yi=2x=2\Re(z) \quad \blacksquare$$

Also here is the proof of $5$

$$z-\bar{z}=x+yi-(x-yi)=2yi=2i\Im(z) \quad \blacksquare$$

So if you introduce coordinates, it's not too hard. By coordinates here, I mean the $x+yi$. And this is what we call the standard form of a complex number. We'll see at the end the polar form is coming up. So that’s properties of conjugates here.

Properties of Modulus (PM)

Definition: The modulus of $z=x+yi$ is the nonegative real number

$$|z|=|x+yi|:= \sqrt{x^2+y^2}$$

So we're taking the length of the number in the plane, that’s basically what's happening here.

The Properties of Modulus, so something to mention here, when we're dealing with modulus and actually with proofs of modulus things, it actually helps to prove things about the square of the modulus because it's a little bit easier to work with. Here dealing with the square root’s a little bit annoying.

Proposition (PM):

1. $|\bar{z}|=|z|$
2. $z\bar{z}=|z|^2$
3. $|z|=0 \Leftrightarrow z=0$
4. $|zw|=|z||w|$
5. $|z+w| \leq |z|+|w|$ (This is called the triangle inequality)

Keep in mind that the modulus is a non-negative real number.

Proof Outlines

So for example let's say question $1$: we have the modulus, or the absolute value, that’s another way to look at it, $|\bar{z}|=|z|$. So if we wanted to prove this one, one way we can do this is square both sides, prove that the squares are equal, and then justify that we can take square roots because it's a non-negative real number. So we don't have to deal with like the multiple solution issue.

For $5$, if you actually draw a picture in the plane of $z+w$, it'll look like… so if I add the size of $z$ plus the size of $w$, it'll look like a triangle when I compare it to the size of $z+w$. I don't think I have a picture here. There's a picture in the notes, you can check that out.

The last three properties define something called the norm. That's not something that we're going to say anything more about other than that sentence. You can check it out in real and complex analysis in a later course if you're interested.

Of these, I'm going to prove only $5$. Again a lot of these can be proved by introducing coordinates. They're not hard. For $2$, the fact that length doesn't change if I reflect about the x-axis, that shouldn't surprise us. $2$ is just an algebra proof, just crunch it in. $3$ is very straightforward, and $4$, again, is an algebra proof, or you could square both sides and use property $2$, and Properties of Conjugates that also works as well.

Proof of $5$

Let's look at $5$, okay, so here's the proof of the triangle inequality. It's the only one that's really involved. I'm going to use that trick that I said before.

To prove that $|z+w| \leq |z|+|w|$, it suffices to prove that

$$|z+w|^2 \leq (|z|+|w|)^2=|z|^2+2|zw|+|w|^2$$

This is true because again, they're non-negative real numbers so if the squares or less than or equal to then the original number is less than or equal to.

So using Properties of Modulus and Properties of Conjugate, what do we have?

$$\begin{align*} |z+w|^2&=(z+w)(\overline{z+w}) &&\text{PM}\\\\ &=(z+w)(\bar{z}+\bar{w}) &&\text{PCJ}\\\\ &=z\bar{z} +z\bar{w} +w\bar{z} +w\bar{w}\\\\ &=|z|^2 +z\bar{w}+\overline{z\bar{w}}+|w|^2 &&\text{PCJ and PM} \end{align*}$$

In the last line to get the value $\overline{z\bar{w}}$ I used the fact that $\bar{\bar{w}}=w$, and I used the fact that the product of the conjugate is the conjugate of the products. So that gives us that $w\bar{z}=\overline{z\bar{w}}$

Now what do we notice here? We have $z\bar{w}+\overline{z\bar{w}}$. If we treat $z\bar{w}$ as some complex number, then this is the complex number plus its complex conjugate. So by Properties of Conjugate, what does that mean?

$$z\bar{w}+\overline{z\bar{w}}=2\Re(z\bar{w}) \leq 2|z\bar{w}|=2|zw|$$

So to explain the $2\Re(z\bar{w}) \leq 2|z\bar{w}|$ step, so if you think about it, right, if you think about $\Re(z\bar{w})$, and then you're adding a little component, then you're going to add a little bit to the length, okay, and that's what's happening here.

I mean we can prove this by introducing coordinates as well, but I think that the idea is pretty clear, right? If you have just the real component, then your length must be smaller than if I had the real and an imaginary component. It could be equal though, right? You could have a real number out of this.

Hence,

$$|z+w|^2=|z|^2+z\bar{w}+\overline{z\bar{w}}+|w|^2 \leq |z|^2+2|zw|+|w|^2 \quad \blacksquare$$

So an interesting little proof, I suggest playing around with it, maybe drawing a couple pictures is probably a good idea if you really want to understand the triangle inequality. It is a triangle inequality, if you draw pictures it does look like a triangle, but again I'll leave it for you to check that out in the notes.

Polar Coordinates

Polar coordinates, the last thing we talked about this week was transferring things in standard form to polar coordinates. You can also go the other way too, it's not too difficult, and we'll see that in a minute. But let's just go through and talk a little bit about polar coordinates.

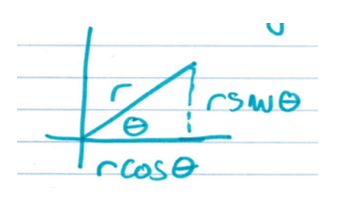
So a point in the plane can correspond to a length and an angle. So here's a little picture on the first quadrant. My length here is that $r$ value, the length from the origin to the point. My $\theta$ is the angle that it makes from the positive $x$-axis to the line, and from here we can see a little trigonometry, right? Our $r\sin\theta$ is going to be the length of the altitude here, and then the length on the $x$-axis is going to be $r\cos\theta$.

Example

$(r,\theta)=(3,\frac{\pi}{4})$ corresponds to

$$3\cos\left(\frac{\pi}{4}\right)+i\left(3\sin\left(\frac{\pi}{4}\right)\right)=\frac{3}{\sqrt{2}}+\frac{3}{\sqrt{2}}i$$

via the picture

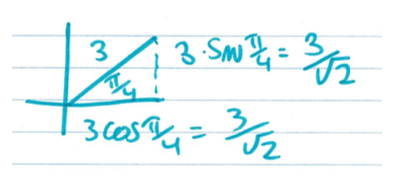
So if we draw a little picture here, we have $r=3$, and then $\theta=\displaystyle\frac{\pi}{4}$, and we know that, again, for $\displaystyle\frac{\pi}{4}$, we have a $\displaystyle\frac{\pi}{4}$, $\displaystyle\frac{\pi}{4}$, $\displaystyle\frac{\pi}{2}$ triangle. So $1$, $1$, $\sqrt{2}$ are the side ratio lengths, but if the $\sqrt{2}$ side is equal to $3$, then each of these side lengths should be $3\sqrt{2}$. That's what we get.

So there's a $(0,0)$ point that we have to deal with, but we're going to ignore that issue for now. $(0,0)$ doesn't really correspond - well, I mean, I guess the $r$ value is $0$ and the $\theta$ is $0$, I guess. I mean you could argue that $\theta$ value can be anything. So let’s exclude $(0,0)$ from the argument. We can see that we can correspond every pair, $(r,\theta)$, to a standard form point and every standard form point to a pair, $(r,\theta)$.

Converting From Standard to Polar Form

So how do we see that? Given $z=x+yi$, we see that

$$r=|z|=\sqrt{x^2+y^2}\\\\ \theta=\arccos\left(\frac{x}{r}\right)=\arcsin\left(\frac{y}{r}\right)=\arctan\left(\frac{y}{x}\right)$$

So something we have to watch out for here. So pictorially, it makes sense, right, $\tan\theta=\displaystyle\frac{y}{x}$, that's true. But to say $\theta=\arctan\left(\displaystyle\frac{y}{x}\right)$, it's actually being a little bit incorrect, there's a couple of problems here.

What are some of the problems that come up? So $\tan\theta=\displaystyle\frac{y}{x}$, but we have some issues. So for example, like what is $\tan(90^{\circ})$, right? That's a problem.

So the things on the imaginary axis, we can just do by eyeballing. We don't need to compute $\arctan$ of something, right, we just know that on the imaginary axis that were either $90^{\circ}$ or $270^{\circ}$, so $\displaystyle\frac{\pi}{2}$, or $\displaystyle\frac{3\pi}{2}$.

Now when you compute $\theta=\arctan\left(\displaystyle\frac{y}{x}\right)$, you have to be a little bit careful because what's the range of $\arctan$? The range of $\arctan$ is $\displaystyle -\frac{\pi}{2}$ to $\displaystyle\frac{\pi}{2}$, not including $\displaystyle -\frac{\pi}{2}$ and $\displaystyle \frac{\pi}{2}$, but we already talked about $\displaystyle-\frac{\pi}{2}$ and $\displaystyle \frac{\pi}{2}$.

So the range is $\left(\displaystyle-\frac{\pi}{2},\displaystyle \frac{\pi}{2}\right)$, but however, we have points that could live, you know, let's say $\pi$ degrees away from the $x$-axis. So we have to be a little bit careful, and how we account for this is we just have to double check at the end, when we do this computation, that we either want $\theta$ to be either $\arctan\left(\displaystyle\frac{y}{x}\right)$, or $\pi+\arctan\left(\displaystyle\frac{y}{x}\right)$, depending on what quadrant we’re in.

That's the thing we'll see in the next example, and hopefully that'll clarify what I mean here, okay? So the modulus, the length, of our complex number, that's very easy to determine. $\sqrt{x^2+y^2}$. The thing that changes here though is possibly $\theta$, right, $\theta$ is $\arctan\left(\displaystyle\frac{y}{x}\right)$, or $\pi+\arctan\left(\displaystyle\frac{y}{x}\right)$ depending on where we are.

Example

Write $z=\sqrt{6}+\sqrt{2}i$ using polar coordinates. What about $-z$?

Solution

So write $-z$ as well. What's the difference? Spend a couple minutes, try it. Use the formulas on the previous page. Let's give this a shot.

So $|z|$ is always easy to compute, $|z|=r=\sqrt{\sqrt{6}^2+\sqrt{2}^2}=\sqrt{8}=2\sqrt{2}$. The angle that we're computing is $\arctan\left(\displaystyle\frac{y}{x}\right)= \arctan\left(\displaystyle\frac{\sqrt{2}}{\sqrt{6}}\right)$, and if we do that, we get $\arctan\left(\displaystyle\frac{1}{\sqrt{3}}\right)= \displaystyle\frac{\pi}{6}$.

That again, you can see these things, so if these things are unfamiliar to you, these trig identities, I mean draw a picture, of course, and if you don't remember how to do that, I would advise checking out the CEMC courseware. There's some good material on there.

So thus, what do we know from this? So, the perceived angle is $\displaystyle\frac{\pi}{6}$ and if we think about where this $z$ lives, it has a positive $x$ value and a positive $y$ value, so it's in the first quadrant. $\displaystyle\frac{\pi}{6}$ corresponds to a point in the first quadrant, so we're okay.

So thus, $(r,\theta)=(2\sqrt{2},\displaystyle\frac{\pi}{6})$ is the polar coordinate for $z$.

Now what about for $-z$? If you think about $-z$, you're going to get the same answers here. You're going to get that $r=2\sqrt{2}$, and if I take $\arctan\left(\displaystyle\frac{-\sqrt{2}}{-\sqrt{6}}\right)$, that's $\displaystyle\frac{\pi}{6}$.

So what happened here? What are we doing? What's really going on? So we have to be careful, and what's happening here is that instead of being in the first quadrant, we're all the way around in the third quadrant. We've looped around by $180^{\circ}$.

So well now to get your final answer, instead of saying it’s $\displaystyle\frac{\pi}{6}$, add $\pi$ to it. That'll give us $\displaystyle\frac{7\pi}{6}$, and that's where our $-z$ point is.

So that's it for converting standard to polar form, that's it for modulus and Properties of Conjugates and complex numbers. It’s a brief overview, in this video, but I think the ideas are fairly clear.

A lot of you have seen this before as well, so I'm not too, too worried about spending a lot of time with the gory details. If anything here is unclear, or if you don't know anything that I've said, it's a good idea to work it out. Try to pencil and paper out some of the proofs, try introducing coordinates, try doing some of these problems without coordinates if you can.

Some of the proofs, especially in the Properties of Modulus, there’s a couple of those proofs that you can do without going to coordinates. Just remember that when you're dealing with like a length, a modulus, you can square both sides and that usually makes the computation easier. That's all I have to say, so thank you very much for listening and good luck.