CCC Week 9 Part 1 RSA

Introduction

Hello everyone. Welcome to Week 9 of Carmen's Core Concepts, my name is Carmen Bruni. In this video, this is part 1 of Week 9, we're going to talk about RSA which is an encryption scheme, a public key cryptography scheme, and it's very well known, very well used still, even though it's somewhat 40 years old or so.

RSA stands for Rivest, Shamir, and Aldeman, the 3 people who created the algorithm. Something to keep in mind, so I do want to say something, that this is an RSA video. There are lots out there, this isn't unique by any stretch of the imagination. I don't even claim that this is the best video in RSA out there. There are probably others that are much, much more practiced, rehearsed, well-informed, whatever.

What I do want to say though is that I don't know of any video that does exactly this approach, and the approach that I'm going to take is that I'm going to talk about why RSA needs two primes as opposed to just having one. So what I'm going to do is I'm going to explain like an RSA with one prime, that's going to be called an exponentiation cipher, and then I'm going to talk about what happens when we have 2 primes.

Table of Contents

The first four points are going to talk about exponentiation ciphers. Then we're going to talk about the good, the bad, and the ugly with exponentiation ciphers, and we’re going to talk about the RSA algorithm. We'll talk a little bit about security and food for thought and an example at the end.

Exponentiation Ciphers

Recall Public Key Crypotography

Let's actually start by recalling the public key cryptography scheme.

So suppose Alice and Bob want to share a message, but there's an eavesdropper, Eve, watching their communications, and in our situation, we're going to assume that Eve is just looking at the insecure channel between Alice and Bob.

So Alice will publish some public information, and Bob will try to send Alice a message by encrypting this message using the public information, and Eve will be able to see the public information and the encrypted message, $C$. And Alice’s job is going to be to create a scheme where she can decode the message sent from Bob, and so that Eve also cannot decode the message.

Public Key Diagram

How Exponentiation Ciphers Work

How are we going to do it? We're going to try to do that first by an exponentiation cipher, okay? And in an exponentiation cipher, so maybe a little bit of thought before we go into this, exponentiation cipher you should be thinking, “Okay, I need to take exponents somewhere. I need to do an exponentiation at some point,” and it turns out that that's true. We do need to do exponentiation, which we will see where that comes into play in a minute.

So in this encryption scheme, Alice is going to choose a large prime $p$, and an integer $e$ satisfying:

$$1 < e <(p-1) \qquad \text{and} \qquad \gcd(e,p-1)=1$$

Alice then makes the pair, $(e,p)$, public and she's going to compute her private key, $d$, and her private key, d, satisfies

$$1 < d < (p-1) \qquad \text{and} \qquad ed\equiv 1 \pmod {(p-1)}$$

So why do we not want to choose $e=p-1$? The reason why is if you choose $e=p-1$, then $d=p-1$ and you'd like $e$ and $d$ to be distinct. So we're going to just avoid that by just not choosing $e=p-1$.

We also don't want to choose $e=1$, because then we're not actually going to be encrypting anything. We're going to be taking a message to the power of $e$, and so if $e=1$, that's kind of boring.

Something to note, that even if $p$ is a large prime, the $e^{-1}$ can be computed very quickly using the Extended Euclidean Algorithm. The reason why we require $\gcd(e,(p-1))=1$ is so that $e$ is invertible $\bmod {p-1}$, so that's something to keep in mind as well. So we need the $e^{-1} \bmod {p-1}$ to exists, we'll see why in a minute.

To send a message, $M$, to Alice, and this message, $M$, is going to be an integer between $0$ and $p-1$ inclusive. Bob is going to compute a ciphertext, $C$, satisfying:

$$0 \leq C < p \qquad \text{and} \qquad C\equiv M^e \pmod p$$

Bob will then send $C$ to Alice. So keep in mind, what can Eve see? Eve can see $e$, $p$, and $C$, which we'll see in the next diagram.

Now what is Alice going to do to decrypt? Alice is going to take that message, $C$, and compute $C^d \pmod p$ with $0 \leq R < p$.

So here's the encryption scheme. What things do we need to know? So first thing we need to do is we need to prove something about $R$. So $R \equiv C^d$, we need to prove that $R \equiv M$, that’s something we need to do. It's not too hard, but we will need to actually compute that.

If Bob chooses $C=0$, then $M^e=0$. If Bob chooses $C=1$, then $M^e=1$. Those are kind of bad messages to pick, so maybe you want to restrict those, maybe you don’t. The scheme works with those two things, so I'm going to just include them just for a theoretical sense, but you probably want to avoid them in practice.

Exponentiation Cipher Diagram

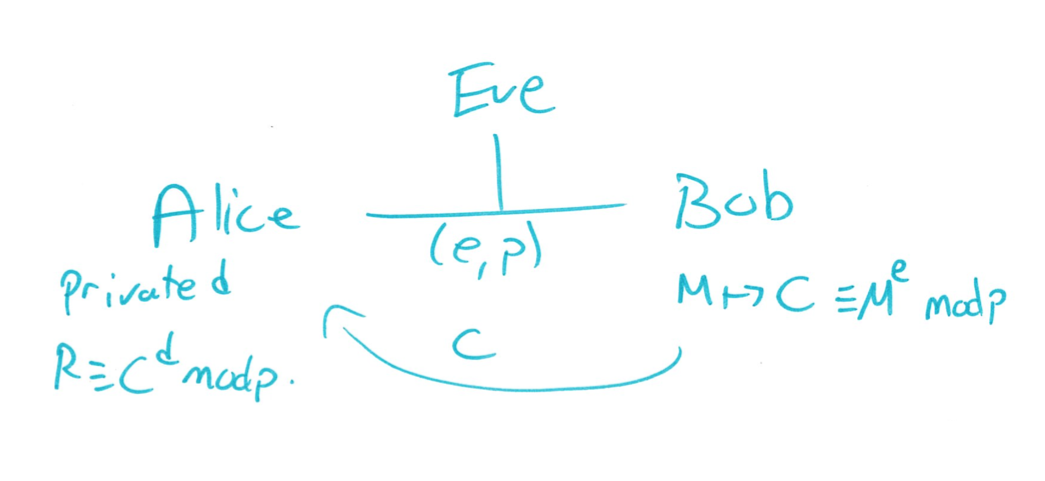
Let's head to the diagram before we head to the proof. So I like to draw the diagram just to remind us of what the situation is.

So Alice computed $e$ and $p$, made that public, computed a private $d=e^{-1} \pmod {p-1}$. $e$ and $p$ are public, Eve and Bob know it, Bob takes his private message, $M$, an integer between $0$ and $p-1$, and computes $C=m^e \pmod p$.

Bob then sends $C$ across the unsecured channel, so Eve knows $e$, $p$, and $C$. Now Alice gets the $C$, and Alice knows $d$, so Alice is going to compute $R \equiv C^d \pmod p$.

Notes on Exponentiation Ciphers

Now something to think about in this scheme, so Eve gets $e$, $p$, and $C$, so something to note is okay well if Eve has $C$, can she compute $M$? Basically what she's trying to ask is, “Can I compute $\sqrt[e]{C} \pmod p$?” And it turns out that this happens to be a difficult problem.

Just to see an example, suppose I told you that $M^6 \equiv 9 \pmod {11}$, and I asked you to determine what $M$ was, okay? How would you do that? I mean really the only way that you're going to be able to even try it is by just plugging in values for $M$. There's a lot of possible values for $M$ if $p$ is large, so this doesn't seem like a very efficient attack.

Now $11$ is small enough that you could probably reason that I believe the answer should be $2$. $2^6=64 \equiv 9 \pmod {11}$. So that one's fairly easy, but you could imagine, like I mean if I ask you the same question $M^6 \equiv 5 \pmod {11}$. What's the answer? I don't know. I mean so you can imagine the situation being very difficult. This is a tough problem to solve; computing $e$-th roots $\bmod p$. At least that’s what we believe.

Exponentiation Ciphers Main Proposition

Proposition: $R \equiv M \pmod p$

From this we're going to conclude that $R=M$ because of the restrictions on $R$ and $M$. $0 \leq R,M < p$, so that will force them to be equal if they're congruent $\bmod p$.

Take a minute, try to prove this. If you prove this without going back in the slides, it shows that you really understand exponentiation ciphers, so hopefully you can do that. If not, go back to the previous slides, check out exponentiation ciphers, and see if you can prove that $R\equiv M \pmod p$.

Proof

Let's take a look at the proof. The proof, it needs to be split up into 2 cases, which might not be obvious at first but it will be obvious once we do it, okay?

If $p \mid M$ everything is $0$ and we're done. So we might as well assume that $p \nmid M$ to get to the interesting case.

So from here, recall that $ed \equiv 1 \pmod {p-1}$, and using this, what do we have?

$$\begin{align*} R &\equiv C^d \pmod p\\\\ &\equiv(M^e)^d \pmod p &&\text{by definition of}\,C\\\\ &\equiv M^{ed} \pmod p \end{align*}$$

Well $ed\equiv 1 \pmod {p-1}$, so we can actually use one of the corollaries to Fermat's Little Theorem which says that if $ed\equiv 1 \pmod {p-1}$, then $M^{ed} \equiv M \pmod p$, provided that $\gcd(M,p)=1$, which is the case if $p \nmid M$.

$$\begin{align*} R &\equiv C^d \pmod p\\\\ &\equiv(M^e)^d \pmod p &&\text{by definition of}\,C\\\\ &\equiv M^{ed} \pmod p\\\\ &\equiv M \pmod p &&\text{Corollary to F}\ell\text{T since}\,ed \equiv 1 \pmod {p-1} \quad \blacksquare \end{align*}$$

And we're done. So it's actually a really, really short proof and it uses Fermat's Little Theorem, which is cool. This is one of the reasons why we needed it.

So then therefore, $R=M$ by that argument that I mentioned at the beginning.

The Good, The Bad and The Ugly

This proves that exponentiation ciphers work. Bob can send a message, Alice can decrypt it. So that's the good news, the good news is that this works.

The bad and the ugly is that well…the bad and the ugly actually are kind of the same thing I guess. Eve can compute $d$ just as easily as Alice, right? If Eve knows $p$ and $e$, there's no reason why Eve can't compute $e^{-1} \pmod {p-1}$, right, because Eve knows $p$, so therefore she knows $p-1$. That's not hard.

So our scheme is not secure, this is pretty bad. So you actually wouldn't want to use the scheme in practice because well…it's not secure.

So how do we rectify this problem? How do we solve this problem? What we can do is we can include information instead of about one prime, we can include information about two primes. It might not be obvious why that matters, right? So before we used one prime, the scheme works but it's not secure, and if we include two primes, how does that make the scheme secure? Something to think about. Think about it while we're going through the scheme.

That's what RSA does though. So a single prime exponentiation cipher, we saw. RSA is like a dual prime or two prime exponentiation cipher. So let's think about why this is going to work.

RSA

So RSA. Now Alice chooses two large primes, $p$ and $q$, and selects any integer, $e$, satisfying:

$$1 < e < (p-1)(q-1) \qquad \text{and}\qquad \gcd(e,(p-1)(q-1))=1$$

So before it was just $p-1$, now we have the product $(p-1)(q-1)$, and $e$ is co-prime to $(p-1)(q-1)$. So here's where the two primes are coming in. Alice then makes the pair $(e,n)$, so $n=pq$. So she makes the product and $e$ public, and computes her private key, $d$, satisfying:

$$1 < d < (p-1)(q-1) \qquad\text{and}\qquad ed\equiv 1 \pmod {(p-1)(q-1)}$$

Again, Alice can compute this quickly because she knows $p$, she knows $q$, so she knows $p-1$ and $q-1$, and so she can compute $e^{-1}$ very quickly using the Extended Euclidean Algorithm.

This is a key, key fact. Alice knows $p$ and $q$ so she can compute $p-1$ and $q-1$ quickly. Remember that sentence.

So what does Bob do? Well Bob sends his message. His message, $M$, is between $0$ and $n-1$ or $pq-1$ inclusive. Bob then computes a ciphertext, $C$, satisfying:

$$0 \leq C < pq \qquad\text{and}\qquad C \equiv M^e \pmod {pq}$$

So we're basically reducing $M^e$ to the least non- negative residue. And we're going to send $C$ across the channel. So Eve knows $e$, $n$, and $C$.

Bob then sends $C$ to Alice and Alice then computes $R \equiv C^d \pmod {pq}$.

Now just like before, we’d like to prove that $R=M$. It's going to take a little bit of effort, but we can do it. But this is the scheme, okay? So it's basically just like the one prime situation except we use two primes.

RSA Diagram

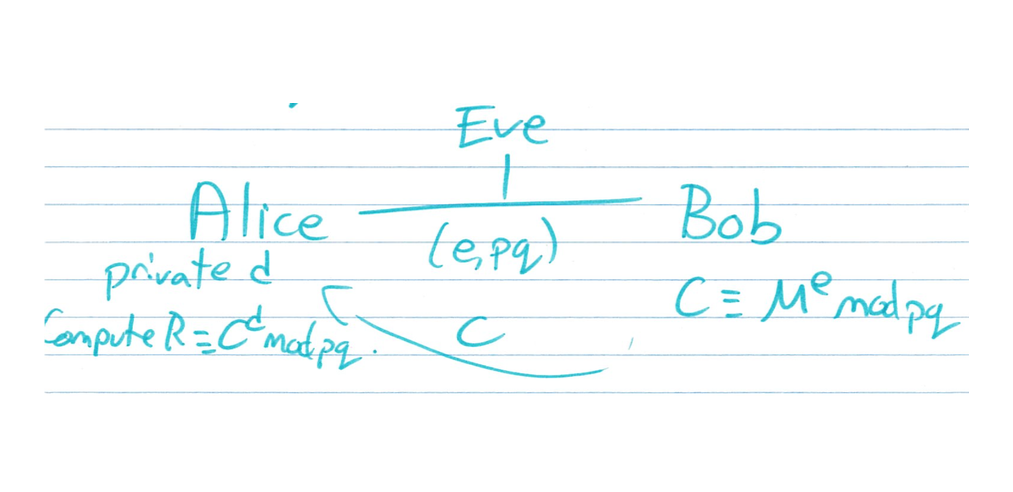
Let's take a look at the diagram. So again, you can see the difference. Eve knows $e$ and $pq=n$. Alice chooses the $p$ and the $q$ and chooses the $e$ and computes the $d$ satisfying $d=e^{-1} \pmod {(p-1)(q-1)}$.

Bob takes his message, $M$, and encrypts it using $M^e \bmod {pq}$ and sends $C$ across the insecure channel, and Alice is trying to compute $R\equiv C^d \pmod {pq}$.

So just like before, computing the $e$-th root of $C$ is going to be difficult $\bmod {pq}$. Again something you can try on your own, but here's the main idea.

RSA Main Proposition

Proposition: $R=M$

Proof

What's the idea that we're going to use here? We're actually going to piggyback off of the exponentiation cipher proof from before.

So step 1 is to reduce to that case twice, and step 2 is to put that together.

So since $ed \equiv 1 \pmod {(p-1)(q-1)}$, Transitivity of Divisibility tells us that:

$$ed \equiv 1 \pmod {p-1} \qquad\text{and}\qquad ed \equiv 1 \pmod {q-1}$$

Since $\gcd(ed,(p-1)(q-1))=1$, GCD from Prime Factorization tells us that $\gcd(ed,p-1)=\gcd(ed,q-1)=1$. In particular, we're really interested in the fact that $\gcd(e,p-1)=\gcd(e,q-1)=1$, but we get both so I might as well mention it.

So thus, as $C \equiv M^e \pmod {pq}$, Spitting the Modulus states that:

$$C \equiv M^e \pmod p \qquad\text{and}\quad C \equiv M^e \pmod q$$

Similarly by Splitting the Modulus again, we have that:

$$R \equiv C^d \pmod p \qquad\text{and}\quad R \equiv C^d \pmod q$$

So now if we look at the situation, pretend you're dividing your screen in half along those “and” symbols, okay? If you look at the left hand side, you have everything $\bmod p$ or $\bmod {p-1}$ that we had in the previous theorem, and if you look at the other side we have everything $\bmod q$ or $\bmod {q-1}$ that we had in the previous theorem. So if I apply that proposition twice, what am I going to get?

$$R\equiv M \pmod p \qquad\text{and}\qquad R\equiv M \pmod q$$

So that was our goal here. We took the general situation of RSA, split it up into like two single prime situations, and then brought them back by using the previous proposition.

We might have needed to reduce this a little bit more, but that's okay. I'm not going to get into small, small details like that. This is the big picture idea, okay?

So now we have $R\equiv M \pmod p$ and $R \equiv M \pmod q$. We can put it together using Splitting the Modulus or Chinese Remainder Theorem. So you put them together, what do we get?

$$R \equiv M \pmod {pq}$$

However, $0 \leq R,M < pq$ and that shows us that $R=M$ $\quad\blacksquare$

That finishes the proof. So that's the idea behind RSA. So RSA: exponentiation cipher with two primes. If you remember it like that, it might help you to remember this in practice.

Security and Food for Thought

Now let's get to the issue of security. Is this scheme more secure than the single prime exponentiation cipher? The answer is yes, of course. Not just because of its name but because it's actually secure.

Can Eve compute $d$? And before we said, “Well Eve had $e$ and $p$, and so Eve could compute $p-1$, so Eve could compute $e^{-1} \pmod {p-1}$.” But now, Eve only has the product $pq$, so computing $(p-1)(q-1)$ when you only have $pq$ is actually quite difficult. You either have to factor $n$, which is a very hard problem, or do something else that nobody's thought of at this point. Nobody knows how to do this problem. To get $(p-1)(q-1)$ from $pq$.

This problem we believe is hard. There's no proof of this fact. We believe that it's hard, but proving that a problem is hard is not easy. Basically the proof that a problem is hard is that it hasn't been done before, is basically the proof. It's not a great proof, but anyways we do believe that factoring numbers is hard.

Eve could also break RSA if she can solve the problem of computing $M$ given $M^e \pmod n$, but again we know this is a hard problem as well, right? Computing the $e$-th root of $M^e$ is not so easy $\bmod n$.

So let $\varphi (n)$ be the Euler Phi Function. Sometimes this is noted by $\varphi$, sometimes it's just noted by $\phi$. I think I denote it by $\phi$ later instead of $\varphi$ in LaTex. Either way is fine, people will know what you mean.

So I'm not going to define what the Euler Phi Function is, but I am going to say that in the case when $n=pq$ is a product of distinct primes, then $\varphi (n)=(p-1)(q-1)$. It's important that they're distinct. This isn't true about this function if they're not distinct primes.

How does Alice choose primes $p$ and $q$? Well we know that they must be distinct. That’s something that we saw in the proof before, right? We’d split the modulus at the end, or use the Chinese Remainder Theorem, so we need $p$ and $q$ to be distinct.

How does Alice choose these primes? Well it turns out that the way to choose them is actually be very silly. If you want to choose a large prime number, turns out that you should just choose a large number. We should be a little bit smarter, let's choose a large odd number, since we know that large even numbers aren’t prime. So if we choose a large odd number, it turns out that if we choose enough of these numbers, that we're going to eventually pick a prime.

Now how many we have to choose? There's an argument using the Prime Number Theorem which off the top of my head I believe says if you have let's say $p=100$, and you want to know if you can find it a hundred digit prime. If you pick about I think it's around the $75$ mark, it's not exact, but if you pick around $75$ big odd numbers, that's going to be enough to have like a $50/50$ chance that one of them is prime. That’s pretty good, and it's not too hard to pick $75$ large odd numbers.

The one thing you might want to ask is, “Well how hard is it to check if a number is prime?” So clearly it must not be too hard based on what I just told you, right, and it turns out that it's not. There's actually quick-ish algorithms that will determine if a large number is prime or not. They're not insanely fast, but they're good.

In fact they're even better if you allow for something called probable primes, which are primes that are highly likely to be prime, let’s say $99.9999$% likely to be prime, whatever that means. I'm not going to justify what that means, but this is an active area of research: probable primes things like this. Check this out online. There's some pretty interesting stuff.

I believe all of that is true though. My numbers might be off a little bit, especially with the Prime Number Theorem argument off the top my head, but I believe that's roughly correct. Again you should check that out, if you want you can google that argument. I'm sure somebody's done it.

What if Eve wasn't just a passive eavesdropper? So what if Eve could change the data? So instead, let's say Alice publishes her public key and Eve says, “No, no, I don't like that public key. I'm going to publish my public key and pretend that I'm Alice,” and then Bob's going to encrypt using Eve's public key, and then Eve is going to take Bob's message and be like, “Ha I'm going to decrypt it,” and then send the encrypted message to Alice using Alice's public key. So Alice and Bob think everything's working, but actually Eve's in the middle attacking everything.

So there are ways to circumvent that. They involve things like certificates, and identity checks, and things like this. This is a huge active area, I believe for example, Verisign, a company which produces certificates, they're like a billion dollar company I believe, and it just involves the idea of just verifying identities, which is pretty cool and crazy to think that, you know, it's such an important idea but it's not too hard mathematically, and it's actually worth a lot of money. So this is a big active area of research and big active area of interest for people.

What are some advantages to RSA? We believe it's secure, it's pretty quick, encryption and decryption can be done with the same sort of black box, right? Just taking powers of numbers, and they can be done very quickly using the Square and Multiply Algorithm. I didn't mention that, but we can use the Square and Multiply Algorithm to do it pretty quickly.

RSA Examples

Let $p=2$, $q=11$, and $e=3$.

1. Compute $n, \phi (n)$ and $d$.
2. Compute $C \equiv M^e \pmod n$ when $M=8$.
3. Compute $R \equiv C^d \pmod n$ when $C=6$.

Take a minute. Try to solve these three problems.

Solutions

$n, \phi (n)$ and $d$ are pretty simple. $n=pq=2(11)=22$. $\phi (n)=(p-1)(q-1)=1(10)=10.$ $d=e^{-1} \pmod {\phi(n)}$. It turns out if you do that computation, so you want to solve $3d \equiv 1 \pmod {10}$. Check out all $10$ numbers, so $3, 6, 9, 12,$ which is $2$, $15$ which is $5$, $18$ which is $8$, $21$ which is $1 \bmod 10$.

So how did I get from $3$ to $21$? I multiplied by $7$, so $d \equiv 7 \pmod {10}$.

So for part 2, we’d like to compute $M^e \pmod n$, when $M=8$. So let's do that.

$$\begin{align*} C \equiv M^e &\equiv 8^3 \pmod {22}\\\\ &\equiv 8 \cdot 64 \pmod {22}\\\\ &\equiv 8 \cdot (-2) \pmod {22}\\\\ &\equiv -16 \pmod {22}\\\\ &\equiv 6 \pmod {22} \end{align*}$$

Great, so $C \equiv 6 \pmod {22}$.

Now to solve part 3, there's the easy way to do it, right? We know that $C \equiv 6$, so then if I’m decrypting, I get $R$ and we already proved that $R=M$, so $C^d \equiv 8 \pmod n$, but if you don't want to do it that way, we can actually just compute it by hand, and I should probably do one more computation just so that you see.

$$\begin{align*} R &\equiv C^d \pmod {22}\\\\ &\equiv 6^7 \pmod {22} \end{align*}$$

$6^7$ is big, one way we can split this up is using the Square and Multiply Algorithm. One way to split it up is we can take $6 \cdot (6^2)^3 =6 \cdot (36)^3 \equiv 6 \cdot 14^3 \pmod {22}$, $14$ is still kind of big, maybe it's not the best way to do it. If you're brave and if you know a little bit about small powers, you’ll know $6^3=216$, and that's going to help us here.

$$\begin{align*} R &\equiv C^d \pmod {22}\\\\ &\equiv 6^7 \pmod {22}\\\\ &\equiv 6 \cdot (6^3)^2 \pmod {22}\\\\ &\equiv 6 \cdot (216)^2 \pmod {22}\\\\ &\equiv 6 \cdot (-4)^2 \pmod {22}\\\\ &\equiv 6 \cdot 16 \pmod {22}\\\\ &\equiv 6 \cdot (-6) \pmod {22}\\\\ &\equiv -36 \pmod {22}\\\\ &\equiv 8 \pmod {22} \end{align*}$$

Now you might argue how do I know that in hindsight? Well okay, I mean, you practice, you gamble, you take chances, and sometimes you're rewarded by taking a chance and computing $6^3$. And that's it.

So hopefully this video gave you a little bit of insight to the RSA algorithm. Hopefully the example helps you to understand a little bit, and hopefully you understand how to go from a single prime exponentiation cipher to a two prime RSA algorithm. So that’s great, that's all I have to say. Thank you very much for your time and good luck.