CCC Week 11 Part 2

Introduction

Hello everyone. Welcome to Week 11 part 2 of Carmen's Core Concepts, my name is Carmen Bruni. In these video series, we go through concepts in Math 135 that we talked about through the week. This being part 2, it is the second part of my two-part video for Week 11.

What I decided to do this week is I decided to break apart the theory from the applications. So in part 1, we talked a lot about theorems, and proofs, and statements, and here in part 2 we're going to talk about how to use the theorems to actually prove things in mathematics.

Table of Contents

Again here's the table of contents. We're going to talk about irreducibility, using long division, some other techniques for finding roots. We'll talk about a rational roots example, a conjugate roots example, and rationality of numbers.

Definition of Irreducibile

So first I'd like to start off with the definition of irreducible. This is something that has often been in assignments, and I think I'm going to move this into my lectures, and it talks about what it means to be irreducible because often what we do in this course, or often what we do with polynomials, is we try to factor them. And the question becomes, “Well how far can I factor?” and the answer is, “Well you factor into irreducible polynomials.” Well what's an irreducible polynomial?

Definition: Let $\mathbb{F}$ be a field. We say that a polynomial of positive degree in $\mathbb{F}[x]$ is reducible in $\mathbb{F}[x]$ when it can be written as the product of two polynomials in $\mathbb{F}[x]$ of positive degree. Otherwise we say that the polynomial is irreducible in $\mathbb{F}[x]$.

For example, $x^2+1$ is irreducible in $\mathbb{R}[x]$. because it doesn't factor anymore. There's no linear factors, but it's reducible over $\mathbb{C}[x]$. There's clearly two linear factors, $x-i$ and $x+i$. So we can rewrite $x^2+1=(x-i)(x+i)$, but we can't do that over $\mathbb{R}$. There's no way to write it as the product of two polynomials of positive degree.

So notice that if we can factor a quadratic into a product of irreducibles it must factor as 2 linear components, and we don't have that for $x^2+1$ because again by the Factor Theorem, we know this has no roots over $\mathbb{R}$ and so, by the Factor Theorem it can't have a linear factor.

The Field Matters

So one thing I want to talk about now is that the field that you're doing these operations with matters. So in the previous example, we saw one example, but here's a little bit more complicated example.

So let's factor this polynomial, $z^z-z^4-z^3+z^2-2z+2$.

$$\text{Over}\,\mathbb{C},(z-i)(z+i)(z-\sqrt{2})(z+\sqrt{2})(z-1)$$

But as we notice, not all of these elements live inside the real numbers. So over the real numbers, we can't actually factor the first two components here, $z-i$ and $z+i$. So we have to bring those together.

$$\text{Over}\,\mathbb{R},(z^2+1)(z-\sqrt{2})(z+\sqrt{2})(z-1)$$

So that's our factorization over R, and over $\mathbb{Q}$, we don't have $\sqrt{2}$. $\sqrt{2}$ is irrational as we've seen in this course. So we have to merge the middle two products together.

$$\text{Over}\,\mathbb{Q},(z^2+1)(z^2-2)(z-1)$$

So here we go, here's our irreducible factorization over $\mathbb{Q}$, there's our irreducible factorization over $\mathbb{R}$, and the top one’s our irreducible factorization over $\mathbb{C}$.

So again, it does depend on what field you’re factoring over. This should make sense, right, not all of these fields have the same elements, so depending on where I factor, depends on how this factors as a polynomial.

By the way, this answer would also be different over finite fields. I didn't talk about it, but if I factored this over, let's say, $\mathbb{Z}_5$, I would get a different factorization.

So for example, $z^2+1$ factors over $\mathbb{Z}_5$. $2$ and $3$ are both roots of $z^2+1$ in $\mathbb{Z}_5$, so there would be a $z-2$, and a $z-3$ factor from this, and $z^2-2$, this is irreducible over $\mathbb{Z}_5$. We'll talk about this in a minute.

$z^2-2$ has no roots, I mean that's maybe the easiest way to say this for now, right, if I plug in the numbers from $0$ to $4$, none of these are $0$ and hence it has no roots since it has no linear factors by the Factor Theorem. Okay, so the field matters when we're factoring, it changes the answer a lot.

Using Long Division

Let's see an example. My example here is:

$$\text{Factor}\,f(x)=x^4-2x^3+3x^2-4x+2\,\text{over}\,\mathbb{Z}_7$$

Take a minute, try to see if you can factor this.

So what should we try to do? Well let's try to find a factor. We don't have too many techniques at this point, so let's just guess and check. So if I'm guessing and checking, some simple numbers to plug in should be $0$ and $\pm 1$, for sure to start, and then get a little bit higher, and then hopefully you find one by then.

Here we notice that $1-2+3-4+2=0$, and so $1$ is a root. So the sum of the coefficients is $0$ if and only if $1$ is a root, it's an interesting little fun exercise to play with yourself, but it's not too hard to prove.

Okay so we have a root, so let's take that root and let's factor it out. So we know that $x-1$ is a factor, we can use long division to get that factor out of there, and so we have that

$$f(x)=(x-1)(x^3-x^2+2x-2)$$

So we'll do a long division example later, I don't want to do one now. There's also lots on the Math 135 Resources Page that you can check out. I think I do at least two there.

Now we look at this new polynomial, and now it's of smaller degree and we repeat the same process. We say, “Okay well can I factor this polynomial?” And the answer is yes we can. The sum of the coefficients is still $0$, $1-2+2-2=0$.

So now what we can do is we can either do long division again, or we can actually group this by doing the following:

$$\begin{align*} f(x)&=(x-1)(x^3-x^2+2x-2)\\\\ &=(x-1)(x^2(x-1)+2(x-1))\\\\ &=(x-1)(x^2+2)(x-1)\\\\ &=(x-1)^2(x^2+2) \end{align*}$$

Now we have to look at this polynomial and say, “Well can it be factored?” Well if it can be factored, again just like what we talked about in the previous slides, if you can factor a quadratic into irreducible polynomials, there must be two linear factors that multiply together to give me $x^2+2$. But if I have two linear factors and they correspond to roots.

So if this factors over $\mathbb{Z}_7$, then there must be roots in $\mathbb{Z}_7$. So just check all the values to see if there are any roots. There's only $7$ values to check, and the operation is done modulo $7$, it's pretty quick.

$x$	$x^2+2$
$0$	$2$
$1$	$3$
$2$	$6$
$3$	$4$
$4$	$4$
$5$	$6$
$6$	$3$

In particular, none of these are $0$, so therefore $x^2+2$ has no root in $\mathbb{Z}_7$, and the above form is completely factorized. And that's it.

So it gives us a nice little example, there's a couple of things to note here though. So notice that we knew that $x=1$ is a root of this polynomial, but we didn't know how many times $x-1$ was a factor, and the way that we did that was we took that factor, and we factored it out. We got this cubic and then we do this again, okay, and that gave us an $(x-1)^2$. So we saw that $1$ was a root, but we didn't see how many times $1$ was a root.

Multiplicity of Roots

That leads to the concept of multiplicity. So we say that, from the previous example, this root $1$ has multiplicity $2$ because $(x-1)^2$ is a factor of my polynomial, and that gives us this definition.

Definition: The multiplicity of a root $c \in \mathbb{F}$ of $f(x) \in \mathbb{F}[x]$ is the largest $k \in \mathbb{N}$ such that $(x-c)^k$ is a factor of $f(x)$.

Notice that we can take $k$ to be a natural number because we already know that $c$ is a root of my polynomial, and so $k \geq 1$. So for example, the multiplicity of the root $1$ in the last example was $2$.

Okay, so that's multiplicity of roots. We've seen an example of how to factor, but in this example we just basically guessed and hoped that we could find a root. Now one thing to notice that in this particular example, we got lucky that we found a root. It's possible for a quartic polynomial to factor as the product of two quadratic polynomials, and in which case how would we do that?

And it turns out this question, we're not going to talk about this much in this class at least over finite fields, but I mean the question gets a little bit complicated, right? How do I factor this as the product of two irreducible quadratic polynomials. It's going to take a little bit of work. You could try a guess and check method, and that's probably enough for us, but in general, you can sort of see oh this question can be really complicated. Life is pretty good when you have roots but what if this factored as, let's say, $(x^2+2)^2$, then you might not know what the factors are. Anyways something to think about.

Techniques for Finding Roots

So what techniques do we have for finding roots? We've already seen an example and now I'm going to talk about the techniques in general.

Well one thing we can do is we can try to use the Rational Roots Theorem to guess a rational root, depending on what field were in, right? So in the previous example, we were in $\mathbb{Z}_7$. Rational Root Theorem doesn't make much sense there, but we can still try to trial and error and try to guess a root. That's still does make sense.

We could use the Conjugate Roots Theorem, that we'll see in a little bit. We've seen an example already, I talked about it I didn't show you, but we did factoring and grouping. You'll see maybe a couple examples of this later.

We can use long division once we find a root to reduce our problem to something smaller, and if we get down to a quadratic, life is good. We know the quadratic formula, and hopefully we can use that to find roots. So these are the techniques that I would have if I'm trying to factor something. So keep these in mind when you approach a question of factoring polynomials.

Rational Roots Example

Factor $\displaystyle f(x)= x^3-\frac{32}{15}x^2+\frac{1}{5}x+\frac{2}{15}$ as a product of irreducible polynomials over $\mathbb{R}$.

So take a minute, try to see if you can factor this.

The first thing I'd like to note is that we do have this denominator here and it's a little bit complicated to deal with. So what I'd like to do is I’d actually like to get rid of the denominator. Well how do I do that? I can common factor out the denominator.

$$f(x)=\frac{1}{15}(15x^3-32x^2+3x+2)$$

So that'll leave me with a new polynomial with all integer coefficients. And why do I do this? Well once I do that, now I have an integral polynomial that I can now use the Rational Roots Theorem to try to factor.

By the Rational Roots Theorem, we know that the numerator must divide $2$, and the denominator must divide $15$. So the possible roots are:

$$\pm1,\pm\frac{1}{3},\pm\frac{1}{5},\pm\frac{1}{15},2,\pm\frac{2}{3},\pm\frac{2}{5},\pm\frac{2}{15}$$

That leaves us with these $16$ possible roots. That's a lot to try, but the way I would go about this is I would start by attempting the integer ones. So try $\pm 1$ and try $\pm 2$.

Sum of the coefficients isn’t $0$ so $1$ isn't a root. If I plug in $-1$, I see that I get:

$$f(-1)=15(-1)^3-32(-1)^2+3(-1)+2=-15-32+3-2 \neq 0$$

So I know $\pm 1$ doesn't work. Let's try $\pm 2$. If try $2$ here, I'm going to get:

$$f(2)=15(2^3)-32(2)^2+3(2)+2=120-128+6+2=0$$

I found a root, $x=2$. So hence, by the Factor Theorem, $x-2$ is a factor.

Now you have two options at this point: you could keep trying rational roots, or you can do the long division and I'm going to recommend here doing the long division. Why do I recommend doing that? The reason why is that if I do the long division here, I know that I'm going to be left with a quadratic, and I can factor quadratics. I have the quadratic formula so in the worst case, I can always factor a quadratic polynomial. So I have no problems actually doing the long division here because I know if I do that, I'm going to get to something that I can solve quickly.

So do the long division, just roll up your sleeves and do it.

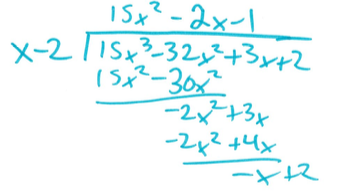
That gives me $15x^2-2x-2$. I know my remainder here is $0$, I didn't actually write the last line because I don't really need to, right, I know that $(-1)(x-2)-(-x+2)=0$ and it's supposed to because I know it's a factor.

So there we go, there's my quotient. Now this is a quadratic polynomial, worst case I plug it into the quadratic formula. The first thing I'm going to try to do though is I'm always going to try to factor, right? If I can actually factor this, then I'm done.

Notice that it does factor and we get:

$$15x^2-2x-1=15x^2-5x+3x-1=5x(3x-1)+1(3x-1)=(5x+1)(3x-1)$$

Beautiful, okay. So I factored this without too much stress at the end, and that's it. Once I have this factorization I'm done.

$$f(x)=\frac{1}{15}(x-2)(5x+1)(3x-1)$$

So notice that, a couple of things, you could have found the rational root $\displaystyle\frac{1}{3}$, or you could have found the rational root $\displaystyle-\frac{1}{5}$ above, and if you've done that you could have factored everything quickly if you found all $3$ roots using the Rational Root Theorem, or if you found one of these other ones, then you could have used long division and then you would have to factor the remaining quadratic, which is perfectly fine, either way is fine. This just gives you an example of how to do this.

Conjugate Roots Example

A conjugate roots example, so how about something a little bit different.

Factor $f(z)=z^4-5z^3+16z^2-9z-13$ over $\mathbb{C}$ into a product of irreducible polynomials given that $2-3i$ is a root.

So here the problem’s a little bit different. Instead of telling you nothing, we actually tell you a root and say, “Hey, can you find the other ones?” Take a minute, give it a shot. Try to see if you can at least come up with a couple of roots and see if you can simplify this.

One thing to note that when we have a real polynomial, so this polynomial is real, and we have a complex root, strictly complex root $2-3i$, we know that this is one root and another root is given by its conjugate. That's the Conjugate Roots Theorem.

So by the Factor Theorem, we know that $(z-(2-3i))$ and $(z-(2+3i))$ must be factors, we multiply them together and we get a quadratic factor of this quartic.

$$(z-(2-3i))(z-(2+3i))=z^2-4z+13$$

So if I do the long division and divide the original quartic by the above quadratic, then I'm left with another quadratic, and I know I can factor those.

$$f(z)=(z^2-4z+13)(z^2-z-1) \quad \text{after long division}$$

Notice that this is over $\mathbb{C}$, so the Fundamental Theorem of Algebra, or CPN, whichever theorem you want to use tells us that this will factor as a product of four linear polynomials.

This last polynomial doesn't factor, but we can use the quadratic formula, right? We have a quadratic, we know that we can find the roots by using the quadratic formula.

$$z=\frac{-(-1) \pm \sqrt{(-1)^2-4(1)(-1)}}{2(1)}=\frac{1 \pm \sqrt{5}}{2}$$

So now we have two more roots, we have the two roots from before, we know all the factors.

$$f(z)=(z-(2-3i))(z-(2+3i))(z-(1+\sqrt{5})/2)(z-(1-\sqrt{5})/2)$$

And that's it. That gives us the factorization of this polynomial.

So there's an example with the conjugate roots. Again so if you're given a root you have a little bit of information, use that to your advantage. Try to find another root using, let's say, the Conjugate Roots Theorem or Rational Roots Theorem, something like this.

Worst case, you divide out and hope for the best, but hopefully you don't divide out by $z-(2-3i)$ because it's going to be a little bit ugly and you're going to have a lot of complex numbers floating around. Because you divided out by the product, we actually ended up with a very, very nice term at the end. So something to think about.

Rationality of Numbers

This is the last topic of this video.

Prove that $\sqrt{5}+\sqrt{3}$ is irrational

Now I often get students very confused about this because it, you know, you just think, “Oh well I know that $\sqrt{5}$ is irrational and $\sqrt{3}$ is irrational, so if I add them it's going to be irrational.” That logic’s wrong, right? I mean $\sqrt{2}$ is irrational and $-\sqrt{2}$ is irrational, but if I add those together I get $0$, which is definitely a rational number, it's an integer.

So you have to be a little bit careful, it's not just enough to say that each of these terms is individually irrational, you need to say something about the sum of these two terms. So you can add two irrational numbers and get something rational, that is possible. Not likely, but it's possible.

Give this a shot, see if you can determine this. If you can't figure this out, you should at least know what kind of proof technique to use. That at least counts for something.

Proof

Hopefully you've at least approached this by using a contradiction argument. Proving that something is irrational is difficult because it's a “not” condition, right? Being irrational means you're not rational, because of that “not” condition, you usually want to proceed by contradiction or contrapositive something like this.

Here we don't have an implication so contrapositive isn’t a possibility, and to be honest with you, contradiction is just always stronger anyway, so I always like to use contradiction.

So I'm going to do a proof by contradiction, we're going to assume that this number is rational, and see where we can go from there.

Assume that $\sqrt{5}+\sqrt{3}=x \in \mathbb{Q}$.

Now what am I going to do? Well it seems natural to want to square, I want to try to get rid of these square roots.

$$(\sqrt{5}+\sqrt{3})^2=5+2\sqrt{15}+3=8+2\sqrt{15}=x^2$$

Now it's a little bit ugly and I still have a square root, but instead of having two square roots I only have one. So it stands to reason that if I isolate for that square root and I square again, I'm going to get rid of the square root.

$$8+2\sqrt{15}=x^2 \Rightarrow 2\sqrt{15}=x^2-8\\\\ (2\sqrt{15})^2=(x^2-8)^2=60=x^4-16x^2+64$$

I'm going to isolate by bringing the 60 over

$$0=x^4-16x^2+4$$

Now what can I do? So by the Rational Roots Theorem, I know that the only possible roots have numerator that's a factor of $4$, and the denominator that's a factor of 1. This only leaves me with 6 roots:

$$\pm 1,\pm 2,\pm 3$$

So a quick check shows that none of these work. You have to actually plug these in and make sure that none of these roots are actually roots of this thing, right? It's possible that $\sqrt{5}+\sqrt{3}=2,4,-1,$, it's possible, a priori, right?

So make sure that none of these roots actually work, and then we have a contradiction. Well why? Well we assume that $x$, which is a rational numbe, is a root of the polynomial that I'm given by $x^4-16x^2+4$.

But of course it's not, right, none of these work and so this rational number, or this number that we assumed as rational, doesn't actually satisfy this polynomial, that gives us a contradiction.

Now what was our contradiction? Well we assumed that this number $\sqrt{5}+\sqrt{3}$ is rational, therefore it must be irrational.

So that's great, hopefully this gave you a little bit of insight as to how to solve some problems where we need to factor, try to find rational roots, or conjugate roots, or proving that numbers are rational.

It's pretty neat stuff, there's lots of applications of this. We just talked about a couple in this video, but hopefully they give you an idea and you can at least try to figure out some new problems based on these ideas. So thank you very much for listening and all the best.