CCC Week 10

Introduction

Hello everyone. Welcome to Week 10 of Carmen's Core Concepts, my name is Carmen Bruni. In this video series, we talk about the weekly topics in Math 135. So without further ado, let's get to it.

Table of Contents

So here we have an outline of the topics discussed in this video. There's going to be a lot of theorems, not too many examples. I think that's okay. The examples are in the notes. There's a lot to some of the examples, so they're worth checking out, but I don't think they're appropriate for this sort of video series.

As a reminder, these videos aren't meant to replace lectures. They’re meant as a supplement to lecture, like if you missed that part of the explanation in one of these theorems then maybe you can catch up on them through these video series.

Polar Multiplication of Complex Numbers (PMCN)

Polar Multiplication of Complex Numbers, so in the last week of lectures, we saw the polar notation for a complex number. So remember that $\text{cis}\,\theta$ means $\cos\theta+i\sin\theta$. $\text{cis}\,$ is just an abbreviation.

Theorem (PMCN): If $z_1=r_1\text{cis}(\theta_1)$ and $z_2=r_2\text{cis}(\theta_2)$, then

$$z_1z_2=r_1r_2\text{cis}(\theta_1+\theta_2)$$

So this gives us a way to multiply two numbers that are in polar form. Remember that polar form is $r\cos\theta+i\sin\theta$.

Proof

If we look at this proof, this proof is actually not too hard. The idea is just sort of a “follow your nose” thing. Take the product of $z_1z_2$, plug it into the $\cos\theta_1 + i\sin\theta_1$ notation, multiply it out, and collect the like-terms.

$$\begin{align*} z_1z_2&=r_1(\cos(\theta_1)+i\sin(\theta_1))r_2(\cos(\theta_2)+i\sin(\theta_2))\\\\ &=r_1r_2(\cos(\theta_1)cos(\theta_2)-\sin(\theta_1)\sin(\theta_2)+i(\cos(\theta_1)\sin(\theta_2)+sin(\theta_1)\cos(\theta_2)))\\\\ &=r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))\\\\ &=r_1r_2\text{cis}(\theta_1+\theta_2)\quad\blacksquare \end{align*}$$

From step $2$ to step $3$, we used trigonometric identities. We used the fact that $\cos(\theta_1)cos(\theta_2)-\sin(\theta_1)\sin(\theta_2)= \cos(\theta_1+\theta_2)$ and $\cos(\theta_1)\sin(\theta_2)+sin(\theta_1)\cos(\theta_2)= \sin(\theta_1+\theta_2)$

And that's it. So very straightforward proof, you start with the left-hand side and show that it equals the right-hand side like we normally do with an equality proof. It's just a matter of expanding the complex numbers in polar form.

De Moivre's Theorem (DMT)

So that’s Polar Multiplication of Complex Numbers, and this, for us, our primary use of this is to discuss De Moivre's theorem, and De Moivre’s theorem, what does it say?

Theorem (DMT): If $\theta \in \mathbb{R}$ and $n \in \mathbb{Z}$, then

$$\text{cis}(\theta)^n=(cos(\theta)+i\sin(\theta))^n=\text{cis}(n\theta)$$

Proof

The proof of this, it's actually pretty clever. What we're going to do is we're actually going to use induction, which is strange because we're over the integers and not over the natural numbers.

Actually the induction proof I'm not going to do because it's actually pretty straightforward and just uses Polar Multiplication of Complex Numbers. So the idea is take off the $n=0$ case, use induction on the positive integers, and then what do we do for the negative integers?

Well the negative integers, we're going to use a little trick. So if $n$ is negative, we're going to write $n=-m$ for some positive number $m$, then:

$$\begin{align*} \text{cis}(\theta)^n&=\text{cis}(\theta)^{-m}\\\\ &=(\text{cis}(\theta)^m)^{-1} \end{align*}$$

Well by induction the positive cases are true, and $m$ is positive, so

$$\begin{align*} \text{cis}(\theta)^n&=\text{cis}(\theta)^{-m}\\\\ &=(\text{cis}(\theta)^m)^{-1}\\\\ &=\text{cis}(m\theta)^{-1} \end{align*}$$

We know how to invert this. We can invert this by using $z^{-1}=\displaystyle\frac{\bar{z}}{|z|^2}$.

$$\begin{align*} \text{cis}(\theta)^n&=\text{cis}(\theta)^{-m}\\\\ &=(\text{cis}(\theta)^m)^{-1}\\\\ &=\text{cis}(m\theta)^{-1}\\\\ &=\frac{\cos(m\theta)-i\sin(m\theta)}{\cos^2(m\theta)+\sin^2(m\theta)} \end{align*}$$

This is a nice little trick when you're dealing with Properties of Modulus. And the bottom, which is $\cos^2(m\theta)+\sin^2(m\theta)$ that's $1$. That's a trigonometric identity, that’s the Pythagorean Identity. So what do we get?

$$\begin{align*} \text{cis}(\theta)^n&=\text{cis}(\theta)^{-m}\\\\ &=(\text{cis}(\theta)^m)^{-1}\\\\ &=\text{cis}(m\theta)^{-1}\\\\ &=\frac{\cos(m\theta)-i\sin(m\theta)}{\cos^2(m\theta)+\sin^2(m\theta)}\\\\ &=\cos(m\theta)-i\sin(m\theta) \end{align*}$$

And now what happens here? So now, this isn't really what we wanted, right? We really wanted this to be $-m$ because we want this to be $\cos(n\theta)-i\sin(n\theta)$. Here we have $m$ instead of $n$.

We can use the fact that $\cos$ is an even function, so $\cos(m\theta)=\cos(-m\theta)$, and $\sin$ is an odd function. So $-\sin(m\theta)=\sin(-m\theta)$.

Therefore, $\cos(m\theta)-i\sin(m\theta)=\cos(-m\theta)+i\sin(-m\theta)= \cos(n\theta)+i\sin(n\theta) \quad \blacksquare$

That actually proves De Moivre’s Theorem. So, this is the first time we've seen induction used on a question where the variable $n$ ranged over the integers, and it involved breaking it up into the positive integers, doing the induction argument there, isolating the $0$ case, and then looking at the negative case and reducing it to the positive case. Another common trick in mathematics which is pretty neat. So that’s it for De Moivre’s Theorem.

Complex Exponential Function

So complex exponential function, this is another thing we talked about. We talked about this new notation

$$e^{i\theta}:=cos(\theta)+i\sin(\theta)=\text{cis}(\theta)$$

This is extremely useful and widely used. Here we're defining it, but we can actually show there are reasons why this notation is useful and actually is used, and I'm going to give you 3 reasons here.

The first reason is that exponential laws work. The fact that exponential laws work, that's just the statement of Polar Multiplication of Complex Numbers.

Derivative with respect to $\theta$ makes sense, so I'll leave this again as an exercise for you to check and you should do it. If you take the derivative with respect to $\theta$ of the left side, treating $i$ as just some constant number with respect to $\theta$, and you take the derivative of the right side, again treating $i$ as just some number with respect to $\theta$, you're going to get the same answers. So the derivatives makes sense, they agree.

More importantly, the power series agree. So if I take the power series of $e^{i\theta}$, I take the power series of $\cos(\theta)$, I take the power series of $\sin(\theta)$, you see if they actually match up. This is in the sense of complex analysis, so this is something you haven't seen yet.

But something that you should do, when you learn this in calculus, is actually check out the $3$ power series here, and see if you can show that this actually works. So take the power series for $e^x$, and I plug in $i\theta$. Take the power series for $\cos(x)$ and plug in $\theta$. I take the power series for $\sin(x)$, plug in $\theta$ and multiply by $i$, do the arithmetic, you're going to see that these $2$ power series actually agree. There's very good reasons for defining this notation, it's not just cosmetic.

Complex $n$th Roots Theorem (CNRT)

With this week, we went to the Complex nth Roots Theorem. This is sort of one of the big theorems we wanted to get to.

Theorem (CNRT): Any nonzero complex number has exactly $n \in \mathbb{N}$ distinct $n$th roots. The roots lie on a circle of radius $|z|$ centered at the origin and spaced out evenly by angles of $\displaystyle \frac{2\pi}{n}$. Concretely, if $a=re^{i\theta}$, then solutions to $z^n=a$ are given by $\displaystyle z=\sqrt[n]{r}e^{i(\theta+2\pi k)/n}$ for $k \in \{0,1,...,n-1\}$

So if I have some $z^n=a$, then there are exactly $n$ roots to this equation, okay, where $a \in \mathbb{C}$.

This is a really, really powerful theorem, right? So it tells you a little bit about the geometry of such solutions, which is really neat. We'll see this in an example soon. So this theorem gives you a formulaic approach for doing it, and gives you a geometric visualization of what the solution should look like.

So what is it saying? This is actually says a lot, okay? This is once we have one solution, we can find all the other ones. So if you know that $a=re^{i\theta}$, then we know that all the solutions are given by $z=\sqrt[n]{r}e^{i(\theta+2\pi k)/n}$.

So in a sense, you started with our first solution, $\sqrt[n]{r}e^{i(\theta)/n}$. That's our first solution, right, $\sqrt[n]{a}=re^{i\theta}$, gives us the case when $k=0$, and then all the other cases you just add multiples of $\displaystyle \frac{2\pi k}{n}$, where $k$ ranges from 1 to $n-1$. That's pretty neat. A lot easier than in the real case.

$n$th Roots of Unity

Definition: An $n$th root of unity is a complex number $z$ such that $z^n=1$. These are sometimes denoted by $\zeta_n$

So before when we had $z^3=1$, we only had one solution over the reals. But now, if we consider $z$ to be a complex variable, then $z^3=1$ actually has $3$ solutions according to this theorem. And that is something that I will leave for you as an exercise.

So you can actually find all $3$ solutions, right? The first one is $z=1$, so if you factor that out of $z^3-1=0$, you're going to be left with a polynomial $z^2+z+1$, and then you can just find the roots of that and those are going to be the other $2$ complex third roots of unity.

Sometimes these are denoted by $\zeta_n$. We won't do it, we won't talk too much about roots of unity but they are a very, very important part of mathematics.

Example

Roots of unity example:

Find all eight roots of unity in standard form.

So again this is a good exercise to practice. Try it out, see if you can find them based on the previous theorem. See if you can do it without looking at the theorem, and if you can’t, check out the theorem.

Solution

So first I'm going to do this algebraically, and then I'm going to do this pictorially. So we already know a solution to this. We know that $z=1$ is a solution, and from the previous theorem, we know that all other solutions are given by $e^{2\pi ik/8}$ for $k \in \{0,1,...,7\}$

Our first solution was $r=1$ and $\theta=0$, and so $\sqrt[n]{1}=1$, and so once we have that, we plug it in, this is what the previous theorem says.

$$\begin{align*} e^{2\pi i(0)/8}&=\cos(0)+i\sin(0)=1\\\\ e^{2\pi i(1)/8}&=\cos(\pi/4)+i\sin(\pi/4)=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\\\\ e^{2\pi i(2)/8}&=\cos(\pi/2)+i\sin(\pi/2)=i\\\\ e^{2\pi i(3)/8}&=\cos(3\pi/4)+i\sin(3\pi/4)=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\\\\ e^{2\pi i(4)/8}&=\cos(\pi)+i\sin(\pi/=-1\\\\ e^{2\pi i(5)/8}&=\cos(5\pi/4)+i\sin(5\pi/4)=-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i\\\\ e^{2\pi i(6)/8}&=\cos(3\pi/2)+i\sin(3\pi/2)=-i\\\\ e^{2\pi i(7)/8}&=\cos(7\pi/4)+i\sin(7\pi/4)=\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i \end{align*}$$

And all of these values give solution, so we can write them using the $\cos+ i\sin$ notation.

So if we actually just do these computations, this is what we're going to get, and if we look, we can draw a diagram based on these solutions, and the diagram that we're going to get is going something like this.

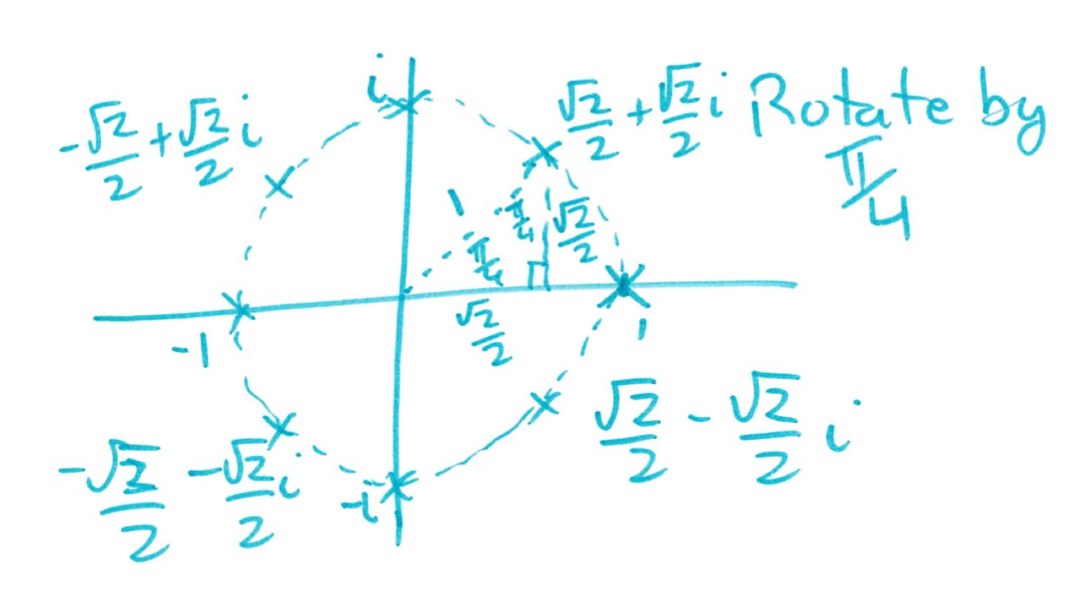
We can also have solved this pictorially as well, right? Remember that we know that once we have one solution, in this case $1$, we can find all other solutions by rotations of $\displaystyle \frac{\pi}{4}$, or in other words, $\displaystyle\frac{2\pi}{8}$. So we have our solution at $1$, we rotate by $45^{\circ}$, or $\displaystyle\frac{\pi}{4}$, we're going to get $\displaystyle\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$, then rotate by another $45^{\circ}$, and another, and another, and another, and another, and so on and so forth.

I want to talk a little bit about this diagram because this diagram is actually pretty cool. So we have $8th$ roots of unity, okay? $8$ is an even number, that's not surprising, but why is that important for this little diagram here?

So whenever I had a solution $i$, or $\displaystyle\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i$, the negation of it was also a solution. That's because if I had $z^8=1$, then $(-z)^8=1$. So here we have the twofold symmetry.

So all of these solutions correspond in pairs on the opposite side. So $1$ corresponds to $-1$, the solution in the second quadrant corresponds to the solution the fourth quadrant, and so on and so forth, that's by negation.

By doing that, that means we only really needed to look at $4$ of the solutions, okay?

Another thing to note, $z^8=1$, then $\bar{z}^8=1$. So I have an answer $z$, then $\bar{z}$ is also a solution, and that's not too hard to see either. The real key to that claim is that $1$ is a real number. So because $1$ is a real number, then if $z$ is a the solution to $z^8=1$, then $\bar{z}$ is also a solution.

So that actually gives us a little bit of twofold symmetry. So it's actually pretty cool. You could actually just compute the solutions in the first quadrant, and along the edge of the first quadrant, and you get all the solutions by just using a little bit of mirror symmetry. That's pretty neat stuff, I think it's pretty cool.

Watch Out! It's a Trap!

What do I mean by this?

Example: Solve $z^5=-16\bar{z}$.

I killed the punch line unfortunately. So what do I mean by it’s a trap? So you might believe, when you look at this, oh well it's $z^5$ so it probably has $5$ solutions, but it actually has $7$ solutions. So this is much different than when you're dealing with a polynomial.

So this thing, as we'll see in a couple minutes, is not a polynomial and that's the problem that we're having here. If it was a polynomial, then it would only have at most $5$ unique solutions. But here, since there's a $\bar{z}$, it's not a polynomial anymore and that might cause it to have more solutions. So you can get some weird things happening in complex number land.

And sometimes we might have no solutions. It’s possible for this equation to not be satisfied. For example take $z+\bar{z}=i$. $z+\bar{z}$ is always going to be real, so there's no solutions.

Proof

So how do we prove this? How do we show there's $7$ solutions? So one thing we note is that $0$ is clearly solution, so we can discount that and we're just looking for$ $6 of the solutions.

So we're going to assume that now $z$ is a non-zero solution to this equation. If we take modulus on both sides and simplify, then we're going to see that

$$|z|^4=16 \Leftrightarrow |z|=2$$

So if you’re solving an equation that you don't know what to do, sometimes it helps to look at the length of the complex number. You can also put this into polar notation and look at the $r$ value that's fine too. I like just taking the modulus on both sides. I think that's a much easier thing to do and understand.

Now the clever thing to do is now, okay, so since $z$ is non-zero, I've already discounted $z=0$, we're going to multiply this original equation by $z$ on either side:

$$\begin{align*} z(z^5)=z^6&=(-16\bar{z})z\\\\ &=-16z\bar{z}\\\\ &=-16|z|^2\\\\ &=-16(4)\\\\ &=-64 \end{align*}$$

And that we know how to solve. $z^6=-64$, that was by CNRT the Complex $n$th Roots Theorem, tells us that there must be $6$ solutions. So we got one solution from $0$, and then $6$ from doing this operation.

So something to watch out for, alright? So you can write down equations with complex things and not get a solution. You can't write down a polynomial in the complex numbers not get a solution, but that we'll talk about later, but if you mix polynomials with complex conjugation, weird things can happen.

Polynomial Ring

Now I want to talk about the polynomial ring, okay, so we're going to finish this week off with a little bit of an introduction to polynomials.

Definition: A polynomial in $x$ over a ring $R$ is an expression of the form

$$a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$$

where $a_0,a_1...a_n \in R$ and $n \geq 0$ is an integer. Denote the set (actually a ring) of all polynomials over $R$ by $R[x]$

I say this is a ring that means I'm going to have to give it an addition and multiplication structure. It's what you think it is, it's what you've been doing all along with polynomials. You've been multiplying polynomials for a long time. Do that operation for multiplication, and addition is, again, what you think, just common factor like-terms with the powers of $x$’s.

As a reminder, what's a ring? Remember that a ring is a set with two operations, addition and multiplication, such that it satisfies some usual axioms. There's additive inverses, you can multiply, there's the distributive property, it's commutative and associative, there's multiplicative and additive identities, things like this.

Typically in this course, we're going to use the definition of a polynomial over a field. This makes our life easier, but I do want to mention that you can define a polynomial ring over a ring. You can even define it more generally, but I think it’s best to do it over a ring like we've done here.

So I mentioned that we will do this over fields. Our fields will include $\mathbb{Q},\mathbb{R}, \mathbb{C}$, and $\mathbb{Z}_p$. Those are the ones that we use, but you could also talk about let's say the integral polynomials, right? Polynomials with integer coefficients and things like that. I just don’t want our definition to restrict us to a field when we know what the word ring means and we can talk about it a little bit more general.

Assorted Definitions

So assorted definitions, so a lot of these you already know. I'm going to just talk about some highlights from this list.

Definition:

1. The coefficient of $a_nx^n$ is $a_n$
2. The term of a polynomial is any $a_ix^i$
3. The degree of a polynomial $\sum_{i=0}^n a_ix^i$ is $n$.
4. The degree of the zero polynomial is undefined (also $-\infty$)
5. A root of a polynomial $p(x) \in \mathbb{F}[x]$is a value $a\in \mathbb{F}$ such that $p(a)=0$.
6. Let $f(x)=\sum_{i=0}^n a_ix^i$ and $h(x)=\sum_{i=0}^n b_ix^i$ be polynomials over $\mathbb{F}[x]$. Then $f(x)=g(x)$ if and only if $a_i=b_i$ for all $i \in \{0,1,...,n\}$
7. $x$ is an indeterminate (or a variable). It has no meaning on its own but can be replaced by a value whenever it makes sense to do so.
8. Operations on polynomials: Addition, Subtraction, Multiplication.

In $3)$, we're assuming here that $a_n \neq 0$, so that gives us the degree of the polynomial. The largest non-zero term. Whatever the power of $x$ is for that term we’ll call that $n$.

In $4)$, we sometimes call it $-\infty$ we'll see why in a little bit, but I think for us we're just going to say it's undefined, that’s perfectly fine for us.

In $6)$, two polynomials are equal if and only if their degrees are the same and each of the coefficients match up, term by term.

In $7)$, $x$ is an indeterminate, so something to keep in mind here, this $x$ thing doesn't have any meaning, okay? One thing we can do is we can attach meaning to $x$, so for example if we look at a complex polynomial and we'd like to evaluate it at a value, that's fine, but that's doing something a little bit more general than just like - so plugging in a number is actually defining a function is kind of what's happening here, and the function takes the polynomial and plugs in instead of $x$ some number and then simplifies it. That's really what's happening there.

So you can view this as a map, it's a little bit abstract but I had a couple of students wondering about, “Okay what is this $x$ thing? Like you keep changing it sometimes, and sometimes you don’t,” and that's really what's happening, okay?

So the polynomial has coefficients over, let's say, a ring or a field, and the $x$ has no meaning, it's just an indeterminate, okay? You can give it meaning, you can plug in values and substitute and things like that, but that's defining a map that goes into a different ring, etc, etc. It's a subtle point, so if you miss that it’s not a huge deal, but if you really understand this and you’re wondering, “Oh why can’t I do these things?” This is what's happening, hopefully it gives you a little bit of an idea.

In $8)$, the operations are what you expect they are. Addition, again, common factor like-terms, multiplication, just foil it out like you normally would.

Division Algorithm for Polynomails (DAP)

The introduction to polynomial says a lot of words and just making sure that we're on the same page of definitions and things like that. One thing that we did do though that was a little bit of substance is the Division Algorithm for Polynomials.

Theorem (DAP): Let $\mathbb{F}$ be a field. If $f(x),g(x) \in \mathbb{F}[x]$ and $g(x)\neq 0$ then there exists unique polynomials $q(x)$ and $r(x)$ in $\mathbb{F}[x]$ such that

$$f(x)=q(x)g(x)+r(x)$$

with $r(x)=0$ or $\deg(r(x)) < \deg(g(x))$

So remember for us if you want to simplify your life a lot, think of a field as $\mathbb{Q},\mathbb{R},\mathbb{C},$ or $\mathbb{Z}_p$.

So the Division Algorithm for Polynomials, this is why sometimes people say that the degree of the $0$ polynomial is $-\infty$. It works in theorems like this for example, right, where $-\infty < \deg(g(x))$ for any $g$ as long as $g$ was non-zero. But we know that $g$ is non-zero, we have that in the theorem.

Notice that this is very similar to Division Algorithm for Integers. We had $a=bq+r$, instead now we have $f(x)=q(x)g(x)+r(x)$, it's the same idea. And it's the same idea, it's kind of like evaluating $\displaystyle\frac{f}{g}$, but we're doing it as $f(x)=q(x)g(x)+r(x)$.

One thing we're going to talk about, maybe I’ll start the next one with this, is Long Division of Polynomials, that's something that's pretty important. Long division for us is going to be a little bit more complicated than normal because our fields might have really weird coefficients, right?

Divide two polynomials over $\mathbb{Z}_7$, let's say. That's a little different, right, than doing it over $\mathbb{R}$. There's a lots of examples of this, I do have a couple of videos where I do do the long division process. You can check them out on the website.

I think that's all I have to say. So thank you very much your time, thanks for listening, and hopefully this video gives you a little bit of insight into Week 10 of Math 135. Take care.