Did Fermat prove this theorem?

No he did not. Fermat claimed to have found a proof of the theorem at an early stage in his career. Much later he spent time and effort proving the cases n=4 and n=5. Had he had a proof to his theorem earlier, there would have been no need for him to study specific cases.

Fermat may have had one of the following ``proofs'' in mind when he wrote his famous comment.

• Fermat discovered and applied the method of infinite descent, which, in particular can be used to prove FLT for n=4. This method can actually be used to prove a stronger statement than FLT for n=4, viz, 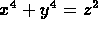has no non-trivial integer solutions. It is possible and even likely that he had an incorrect proof of FLT using this method when he wrote the famous ``theorem''.
• He had a wrong proof in mind. The following proof, proposed first by Lame' was thought to be correct, until Liouville pointed out the flaw, and by Kummer which latter became and expert in the field. It is based on the incorrect assumption that prime decomposition is unique in all domains.

  The incorrect proof goes something like this:

  We only need to consider prime exponents (this is true). So consider 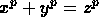. Let r be a primitive p-th root of unity (complex number)

  Then the equation is the same as:

  

  Now consider the ring of the form:

  

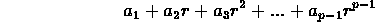
  where each is an integer

  Now if this ring is a unique factorization ring (UFR), then it is true that each of the above factors is relatively prime.

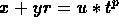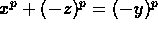  From this it can be proven that each factor is a pth power from which FLT follows. This is usually done by considering two cases, the first where p divides none of x, y, z; the second where p divides some of x, y, z. For the first case, if , where u is a unit in Z[r] and t is in Z[r], it follows that x=y (mod p). Writing the original equation as , it follows in a similar fashion that x = -z (mod p). 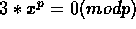Thus which implies and from there p divides one of x or 3|x. But p>3 and p does not divides x; contradiction. The second case is harder.

  The problem is that the above ring is not an UFR in general.

Another argument for the belief that Fermat had no proof --and, furthermore, that he knew that he had no proof-- is that the only place he ever mentioned the result was in that marginal comment in Bachet's Diophantus. If he really thought he had a proof, he would have announced the result publicly, or challenged some English mathematician to prove it. It is likely that he found the flaw in his own proof before he had a chance to announce the result, and never bothered to erase the marginal comment because it never occurred to him that anyone would see it there.

Some other famous mathematicians have speculated on this question. Andre Weil, writes:

Only on one ill-fated occasion did Fermat ever mention a curve of higher genus 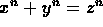, and then hardly remains any doubt that this was due to some misapprehension on his part [ ] for a brief moment perhaps [ ] he must have deluded himself into thinking he had the principle of a general proof.

Winfried Scharlau and Hans Opolka report:

Whether Fermat knew a proof or not has been the subject of many speculations. The truth seems obvious [Fermat's marginal note] was made at the time of his first letters concerning number theory [1637] as far as we know he never repeated his general remark, but repeatedly made the statement for the cases n=3 and 4 and posed these cases as problems to his correspondents [ ] he formulated the case n=3 in a letter to Carcavi in 1659 [ ] All these facts indicate that Fermat quickly became aware of the incompleteness of the [general] ``proof" of 1637. Of course, there was no reason for a public retraction of his privately made conjecture.

However it is important to keep in mind that Fermat's ``proof" predates the Publish or Perish period of scientific research in which we are still living.

References

From Fermat to Minkowski: lectures on the theory of numbers and its historical development. Winfried Scharlau, Hans Opolka. New York, Springer, 1985.

Basic Number Theory. Andre Weil. Berlin, Springer, 1967