


Next: Construction of C
Up: What are numbers?
Previous: Construction of Q
The construction of R is different (and more awkward to understand) because
we must ensure that the cardinality of R is greater than that of Q.
Set c is a Dedekind cut iff
-
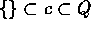 (strict inclusions!)
(strict inclusions!)
- c is closed downward:
if 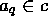 and
and 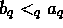 then
then 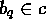
- c has no largest element:
there isn't an element 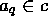 such that
such that 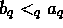 for all
for all 
You can think of a cut as taking a pair of scissors and cutting Q in two
parts such that one part contains all the small numbers and the other part
contains all large numbers. If the part with the small numbers was cut in such
a way that it doesn't have a largest element, it is called a Dedekind cut.
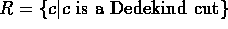 . We will refer to the elements of
R by giving them a subscript . The elements of Q can be embedded as
follows:
. We will refer to the elements of
R by giving them a subscript . The elements of Q can be embedded as
follows: 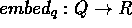 such that
such that  . Furthermore we can define:
. Furthermore we can define:
-
 iff
iff 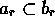 (strict inclusion!)
(strict inclusion!)
-
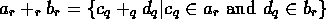
-
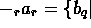 there exists an
there exists an 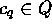 such that
such that 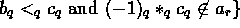
-
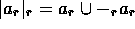
-
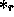 is defined as:
is defined as:
- if not
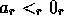 and not
and not 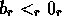
then 
- if
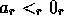 and
and 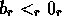 then
then 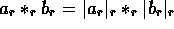
- otherwise
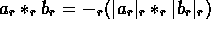
There exists an alternative definition of R using Cauchy sequences: a
Cauchy sequence is a 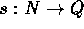 such that
such that 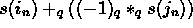 can be made arbitrary near to
can be made arbitrary near to 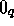 for all
sufficiently large
for all
sufficiently large 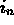 and
and 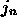 . We will define an equivalence relation
. We will define an equivalence relation
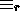 on the set of Cauchy sequences as:
on the set of Cauchy sequences as: 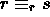 iff
iff 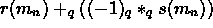 can be made arbitrary close to
can be made arbitrary close to 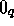 for all
sufficiently large
for all
sufficiently large 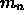 .
. 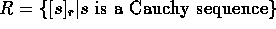 .
Note that this definition is close to ``decimal'' expansions.
.
Note that this definition is close to ``decimal'' expansions.
Alex Lopez-Ortiz
Mon Feb 23 16:26:48 EST 1998
![]() such that
such that ![]() can be made arbitrary near to
can be made arbitrary near to ![]() for all
sufficiently large
for all
sufficiently large ![]() and
and ![]() . We will define an equivalence relation
. We will define an equivalence relation
![]() on the set of Cauchy sequences as:
on the set of Cauchy sequences as: ![]() iff
iff ![]() can be made arbitrary close to
can be made arbitrary close to ![]() for all
sufficiently large
for all
sufficiently large ![]() .
. ![]() .
Note that this definition is close to ``decimal'' expansions.
.
Note that this definition is close to ``decimal'' expansions.