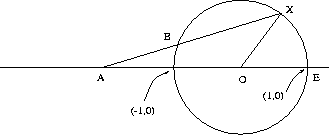
Figure 7.1: Trisection of the Angle with a marked ruler




Theorem 4. The trisection of the angle by an unmarked ruler and compass alone is in general not possible.
This problem, together with Doubling the Cube, Constructing the regular Heptagon and Squaring the Circle were posed by the Greeks in antiquity, and remained open until modern times.
The solution to all of them is rather inelegant from a geometric perspective. No geometric proof has been offered [check?], however, a very clever solution was found using fairly basic results from extension fields and modern algebra.
It turns out that trisecting the angle is equivalent to solving a cubic equation. Constructions with ruler and compass may only compute the solution of a limited set of such equations, even when restricted to integer coefficients. In particular, the equation for theta = 60 degrees cannot be solved by ruler and compass and thus the trisection of the angle is not possible.
It is possible to trisect an angle using a compass and a ruler marked in 2 places.
Suppose X is a point on the unit circle such that angle XOE is the angle we would like to ``trisect''. Draw a line AX through a point A on the x-axis such that |AB| = 1 (which is the same as the radius of the circle), where B is the intersection-point of the line AX with the circle.

Figure 7.1: Trisection of the Angle with a marked ruler
Let theta be angle BAO. Then angle BOA = theta , and angle XBO = angle BXO = 2 theta
Since the sum of the internal angles of a triangle equals pi radians (180 degrees) we have angle XBO + angle BXO + angle BOX = pi , implying 4 theta + angle BOX = pi . Also, we have that angle AOB + angle BOX + angle XOE = pi , implying theta + angle BOX + angle XOE = pi . Since both quantities are equal to pi we obtain
4 theta + angle BOX = theta + angle BOX + angle XOE
From which
3 theta = angle XOE
follows. QED.



