



Next: Name for f(x)^(f(x)) =
Up: Special Numbers and Functions
Previous: Euler's formula: e^(i pi)
According to some Calculus textbooks, 0^0 is an ``indeterminate
form''. When evaluating a limit of the form 0^0, then you need
to know that limits of that form are called ``indeterminate forms'',
and that you need to use a special technique such as L'Hopital's
rule to evaluate them. Otherwise, 0^0 = 1 seems to be the most
useful choice for 0^0. This convention allows us to extend
definitions in different areas of mathematics that otherwise would
require treating 0 as a special case. Notice that 0^0 is a
discontinuity of the function x^y. More importantly, keep
in mind that the value of a function and its limit need not be the
same thing, and functions need not be continous, if that serves
a purpose (see Dirac's delta).
This means that depending on the context where 0^0 occurs, you
might wish to substitute it with 1, indeterminate or
undefined/nonexistent.
Some people feel that giving a value to a function with an
essential discontinuity at a point, such as x^y at (0,0), is
an inelegant patch and should not be done. Others point out
correctly that in mathematics, usefulness and consistency are
very important, and that under these parameters 0^0 = 1 is
the natural choice.
The following is a list of reasons why 0^0 should be 1.
Rotando & Korn show that if f and g are real functions that vanish
at the origin and are analytic at 0 (infinitely differentiable is
not sufficient), then f(x)^(g(x)) approaches 1 as x approaches 0 from
the right.
From Concrete Mathematics p.162 (R. Graham, D. Knuth, O. Patashnik):
Some textbooks leave the quantity 0^0 undefined, because the
functions x^0 and 0^x have different limiting values when x
decreases to 0. But this is a mistake. We must define
x^0 = 1 for all x,
if the binomial theorem is to be valid when x=0, y=0, and/or x=-y.
The theorem is too important to be arbitrarily restricted! By
contrast, the function 0^x is quite unimportant.
Published by Addison-Wesley, 2nd printing Dec, 1988.
As a rule of thumb, one can say that 0^0 = 1, but 0.0^(0.0) is
undefined, meaning that when approaching from a different
direction there is no clearly predetermined value to assign to
0.0^(0.0); but Kahan has argued that 0.0^(0.0) should be 1,
because if f(x), g(x) --> 0 as x approaches some
limit, and f(x) and g(x) are analytic functions, then
f(x)^g(x) --> 1.
The discussion on 0^0 is very old, Euler argues for 0^0 = 1
since a^0 = 1 for a != 0. The controversy raged throughout the
nineteenth century, but was mainly conducted in the pages of the
lesser journals: Grunert's Archiv and Schlomilch's Zeitschrift für
Mathematik und Physik. Consensus has recently been built around
setting the value of 0^0 = 1.
On a discussion of the use of the function 0^(0^x) by an Italian
mathematician named Guglielmo Libri.
[T]he paper [33] did produce several ripples in mathematical
waters when
it originally appeared, because it stirred up a controversy about whether
0^0 is defined. Most mathematicians agreed that 0^0 = 1, but Cauchy
[5, page 70] had listed 0^0 together with other expressions like 0/0 and
oo - oo in a table of undefined forms. Libri's
justification for
the equation 0^0 = 1 was far from convincing, and a commentator
who signed
his name simply ``S'' rose to the attack [45]. August Möbius
[36]
defended Libri, by presenting his former professor's reason for
believing
that 0^0 = 1 (basically a proof that lim_(x --> 0+) x^x = 1). Möbius also
went further and presented a supposed proof that
lim_(x --> 0+) f(x)^(g(x))
whenever lim_(x --> 0+) f(x) = lim_(x --> 0+) g(x) = 0. Of
course ``S'' then
asked [3] whether Möbius knew about functions such as f(x) = e^(-1/x)
and g(x) = x. (And paper [36] was quietly omitted from the historical
record when the collected words of Möbius were ultimately published.)
The debate stopped there, apparently with the conclusion that 0^0 should
be undefined.
But no, no, ten thousand times no! Anybody who wants the binomial theorem
(x + y)^n = sum_(k = 0)^n (n k) x^k y^(n - k)
to hold for at least one nonnegative integer n must believe that
0^0 = 1, for we can plug in x = 0 and y = 1 to get 1 on the left and
0^0 on
the right.
The number of mappings from the empty set to the empty set is 0^0.
It has to be 1.
On the other hand, Cauchy had good reason to consider 0^0 as an undefined
limiting form, in the sense that the limiting value of f(x)^(g(x)) is
not known a priori when f(x) and g(x) approach 0 independently. In
this much stronger sense, the value of 0^0 is less defined than, say, the
value of 0+0. Both Cauchy and Libri were right, but Libri and his
defenders did not understand why truth was on their side.
[3] Anonymous and S... Bemerkungen zu den Aufsatze
überschrieben,
`Beweis der Gleichung 0^0 = 1, nach J. F. Pfaff', im zweiten
Hefte dieses
Bandes, S. 134, Journal für die reine und angewandte Mathematik, 12
(1834), 292--294.
[5] 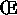 uvres Complètes. Augustin-Louis Cauchy. Cours
d'Analyse de
l'Ecole Royale Polytechnique
(1821). Series 2, volume 3.
uvres Complètes. Augustin-Louis Cauchy. Cours
d'Analyse de
l'Ecole Royale Polytechnique
(1821). Series 2, volume 3.
[33] Guillaume Libri. Mémoire sur les fonctions discontinues,
Journal
für die reine und angewandte Mathematik, 10 (1833), 303--316.
[36] A. F. Möbius. Beweis der Gleichung 0^0 = 1, nach J. F.
Pfaff. Journal für die reine und angewandte Mathematik,
12 (1834),
134--136.
[45] S... Sur la valeur de 0^0. Journal für die reine
und angewandte Mathematik 11, (1834), 272--273.
References
Knuth. Two notes on notation. (AMM 99 no. 5 (May 1992), 403--422).
H. E. Vaughan. The expression '0^0'. Mathematics
Teacher 63 (1970), pp.111-112.
Kahan, W. Branch Cuts for Complex Elementary Functions
or Much Ado about Nothing's Sign Bit, The State of the Art in
Numerical Analysis, editors A. Iserles and M. J. D. Powell, Clarendon
Press, Oxford, pp. 165--212. \
article Louis M. Rotando and Henry Korn.The Indeterminate Form 0^0.
Mathematics Magazine,Vol. 50, No. 1 (January 1977), pp. 41-42.
L. J. Paige,. A note on indeterminate forms. American
Mathematical
Monthly, 61 (1954), 189-190; reprinted in the Mathematical
Association of America's 1969 volume, Selected Papers on Calculus,
pp. 210-211.
Baxley & Hayashi. A note on indeterminate
forms. American Mathematical
Monthly, 85 (1978), pp. 484-486.
Crimes and Misdemeanors in the Computer
Algebra Trade. Notices of the American
Mathematical Society, September 1991, volume 38, number 7,
pp.778-785
In modern mathematics, the string of symbols 0.9999... is understood to
be a shorthand for ``the infinite sum 9/10 + 9/100 + 9/1000 + ...''.
This in turn is shorthand for ``the limit of the sequence of real numbers
9/10, 9/10 + 9/100, 9/10 + 9/100 + 9/1000, ...''. Using the
well-known epsilon-delta definition of the limit (you can find it in any of
the given references on analysis), one can easily show that this limit is 1.
The statement that 0.9999... = 1 is simply an abbreviation of this fact.
0.9999... = sum_(n = 1)^(oo) (9)/(10^n) = lim_(m --> oo) sum_(n = 1)^m (9)/(10^n)
Choose varepsilon > 0. Suppose delta = 1/- log_(10) varepsilon , thus
varepsilon = 10^(-1/delta). For every m > 1/delta we have that
sum_(n = 1)^m (9)/(10^n) - 1 = (1)/(10^m) < (1)/(10^(1/delta)) = varepsilon
So by the varepsilon - delta definition of the limit we have
lim_(m --> oo) sum_(n = 1)^m (9)/(10^n) = 1
Not formal enough? In that case you need to go back to the construction of
the number system. After you have constructed the reals (Cauchy sequences are
well suited for this case, see [Shapiro75]), you can indeed verify that the
preceding proof correctly shows 0.9999... = 1.
An informal argument could be given by noticing that the following sequence
of ``natural'' operations has as a consequence 0.9999... = 1. Therefore
it's ``natural'' to assume 0.9999... = 1.
x = 0.9999....
10 x = 10 * 0.9999...
10 x = 9.9999...
10 x - x = 9.99999... - 0.9999...
Thus 0.9999... = 1.
An even easier argument multiplies both sides of 0.3333... = 1/3 by 3.
The result is 0.9999... = 3/3 = 1.
Another informal argument is to notice that all periodic numbers
such as 0.46464646... are equal to the period divided over the
same number of 9s. Thus 0.46464646... = 46/99. Applying the
same argument to 0.9999... = 9/9 = 1.
Although the three informal arguments might convince you that 0.9999... = 1, they are not complete proofs. Basically, you need to prove that each step
on the way is allowed and is correct. They are also ``clumsy'' ways to prove
the equality since they go around the bush: proving 0.9999... = 1
directly is much easier.
You can even have that while you are proving it the ``clumsy'' way, you get
proof of the result in another way. For instance, in the first argument the
first step is showing that 0.9999... is real indeed. You can do this by
giving the formal proof stated in the beginning of this FAQ question. But
then you have 0.9999... = 1 as corollary. So the rest of the argument is
irrelevant: you already proved what you wanted to prove.
References
R.V. Churchill and J.W. Brown. Complex Variables and Applications. 5^(th) ed., McGraw-Hill, 1990.
E. Hewitt and K. Stromberg. Real and Abstract Analysis. Springer-Verlag, Berlin, 1965.
W. Rudin. Principles of Mathematical Analysis. McGraw-Hill, 1976.
L. Shapiro. Introduction to Abstract Algebra. McGraw-Hill, 1975.




Next: Name for f(x)^(f(x)) =
Up: Special Numbers and Functions
Previous: Euler's formula: e^(i pi)
Alex Lopez-Ortiz
Fri Feb 20 21:45:30 EST 1998
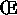 uvres Complètes. Augustin-Louis Cauchy. Cours
d'Analyse de
l'Ecole Royale Polytechnique
(1821). Series 2, volume 3.
uvres Complètes. Augustin-Louis Cauchy. Cours
d'Analyse de
l'Ecole Royale Polytechnique
(1821). Series 2, volume 3.



