 |
Journal of Integer Sequences, Vol. 7 (2004), Article 04.3.1 |
 |
Journal of Integer Sequences, Vol. 7 (2004), Article 04.3.1 |
Abstract:
In this note, we deal with ![]() -arch graphs, a generalization of trees,
which contain
-arch graphs, a generalization of trees,
which contain ![]() -trees as a subclass. We show that the number of
vertex-labelled
-trees as a subclass. We show that the number of
vertex-labelled ![]() -arch graphs with
-arch graphs with ![]() vertices, for a fixed integer
vertices, for a fixed integer ![]() , is
, is
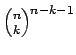 . As far as we know, this is a new integer
sequence. We establish this result with a one-to-one correspondence
relating
. As far as we know, this is a new integer
sequence. We establish this result with a one-to-one correspondence
relating ![]() -arch graphs and words whose letters are
-arch graphs and words whose letters are ![]() -subsets of
the vertex set. This bijection generalises the well-known Prüfer
code for trees. We also recover Cayley's formula
-subsets of
the vertex set. This bijection generalises the well-known Prüfer
code for trees. We also recover Cayley's formula ![]() that counts the number of labelled trees.
that counts the number of labelled trees.
(Concerned with sequences A000272 A098721 A098722 A098723 and A098724.)
Received December 22 2003; revised version received July 1 2004. Published in Journal of Integer Sequences August 2 2004. Minor revisions (to add new sequences), March 16 2005.