Abstract:

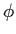
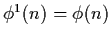
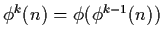
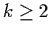
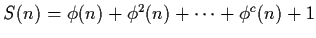
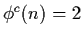
Let n>2 be a positive integer and let $\phi$ denote Euler's totient function. Define $\phi^1(n)=\phi(n)$ and $\phi^k(n)=\phi(\phi^{k-1}(n))$ for all integers $k\ge2$. Define the arithmetic function S by $S(n)=\phi(n)+\phi^2(n)+\cdots+\phi^c(n)+1$, where $\phi^c(n)=2$. We say n is a perfect totient number if S(n)=n. We give a list of known perfect totient numbers, and we give sufficient conditions for the existence of further perfect totient numbers.