Journal of Integer Sequences, Vol. 6 (2003), Article 03.3.7

Binary BBP-Formulae for Logarithms and Generalized Gaussian-Mersenne Primes


Marc Chamberland
Department of Mathematics and Computer Science
Grinnell College
Grinnell, IA 50112
USA

Abstract:

Constants of the form

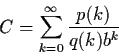
\begin{displaymath}C = \sum_{k=0}^\infty \frac{p(k)}{q(k)b^k} \end{displaymath}

where p and q are integer polynomials, $\deg p <\deg q$, and p(k)/q(k) is non-singular for non-negative k and $b\geq 2$, have special properties. The nth digit (base b) of C may be calculated in (essentially) linear time without computing its preceding digits, and constants of this form are conjectured to be either rational or normal to base b.

This paper constructs such formulae for constants of the form $\log p$for many primes p. This holds for all Gaussian-Mersenne primes and for a larger class of ``generalized Guassian-Mersenne primes''. Finally, connections to Aurifeuillian factorizations are made.

Full version:  pdf,    dvi,    ps,    latex    

(Concerned with sequence A057429 .)

Received July 15, 2003; revised version received October 24, 2003. Published in Journal of Integer Sequences October 25, 2003.

Return to Journal of Integer Sequences home page