Constants of the form
where p and q are integer polynomials,
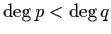 ,
and p(k)/q(k) is
non-singular for non-negative k and
,
and p(k)/q(k) is
non-singular for non-negative k and 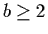 ,
have special properties.
The nth digit (base b) of C may be calculated in (essentially)
linear time without computing its preceding digits, and constants of
this form are conjectured to be either rational or normal to base b.
,
have special properties.
The nth digit (base b) of C may be calculated in (essentially)
linear time without computing its preceding digits, and constants of
this form are conjectured to be either rational or normal to base b.
This paper constructs such formulae for constants of the form 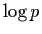 for many primes p. This holds for all Gaussian-Mersenne primes and
for a larger class of ``generalized Guassian-Mersenne primes''.
Finally, connections to Aurifeuillian factorizations are made.
for many primes p. This holds for all Gaussian-Mersenne primes and
for a larger class of ``generalized Guassian-Mersenne primes''.
Finally, connections to Aurifeuillian factorizations are made.
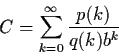
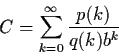
![]() for many primes p. This holds for all Gaussian-Mersenne primes and
for a larger class of ``generalized Guassian-Mersenne primes''.
Finally, connections to Aurifeuillian factorizations are made.
for many primes p. This holds for all Gaussian-Mersenne primes and
for a larger class of ``generalized Guassian-Mersenne primes''.
Finally, connections to Aurifeuillian factorizations are made.