 |
Journal of Integer Sequences, Vol. 22 (2019), Article 19.1.8 |
 |
Journal of Integer Sequences, Vol. 22 (2019), Article 19.1.8 |
James G. Wan
Engineering Systems and Design
Singapore University of Technology and Design
8 Somapah Road, 487372
Singapore
and
School of Mathematical and Physical Sciences
The University of Newcastle
University Drive
Callaghan NSW 2308
Australia
Abstract:
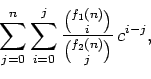
(Concerned with sequences A001008 A002805 A027611 A046825 A046826 A096617 A233470 A234600.)
Received September 25 2018; revised version received January 24 2019. Published in Journal of Integer Sequences, February 15 2019.