An integer composition of a nonnegative integer
n is a tuple
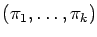
of nonnegative integers whose sum is
n; the
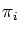
's are
called the
parts of the
composition. For fixed number
k of parts, the number of
f-weighted
integer compositions (also called
f-colored integer
compositions in
the literature), in which each part size
s may occur in
f(
s) different colors, is given by the
extended binomial coefficient
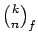
.
We derive several congruence properties for
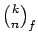
,
most of which are analogous to those for ordinary
binomial coefficients. Among them is the parity of
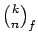
,
Babbage's congruence, Lucas' theorem, etc. We also give congruences
for
cf(
n), the number of
f-weighted integer compositions with
arbitrarily many parts, and for extended binomial coefficient sums.
We close with an application of our results to prime criteria for
weighted integer compositions.
Received September 15 2014;
revised version received February 20 2015.
Published in Journal of Integer Sequences, March 25 2015.

