 |
Journal of Integer Sequences, Vol. 18 (2015), Article 15.3.2 |
 |
Journal of Integer Sequences, Vol. 18 (2015), Article 15.3.2 |
Abstract:
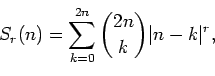
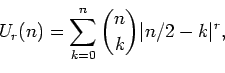
(Concerned with sequences
A000142
A000364
A001147
A001469
A001813
A002105
A009843
A036970
A047053
A054879
A083061
A160485
A245244.)
Received July 16 2014; revised versions received January 18 2015; January 25 2015. Published in Journal of Integer Sequences, January 26 2015.