Journal of Integer Sequences, Vol. 15 (2012), Article 12.8.3

The Generalized Stirling and Bell Numbers Revisited


Toufik Mansour
Department of Mathematics
University of Haifa
31905 Haifa
Israel

Matthias Schork
Camillo-Sitte-Weg 25
60488 Frankfurt
Germany

Mark Shattuck
Department of Mathematics
University of Tennessee
Knoxville, TN 37996
USA

Abstract:

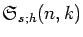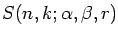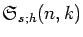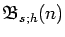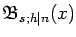The generalized Stirling numbers $\mathfrak{S} _{s;h}(n,k)$ introduced recently by the authors are shown to be a special case of the three parameter family of generalized Stirling numbers $S(n,k;\alpha,\beta,r)$ considered by Hsu and Shiue. From this relation, several properties of $\mathfrak{S} _{s;h}(n,k)$ and the associated Bell numbers $\mathfrak{B} _{s;h}(n)$ and Bell polynomials $\mathfrak{B} _{s;h\vert n}(x)$ are derived. The particular case s=2 and h=-1 corresponding to the meromorphic Weyl algebra is treated explicitly and its connection to Bessel numbers and Bessel polynomials is shown. The dual case s=-1 and h=1 is connected to Hermite polynomials. For the general case, a close connection to the Touchard polynomials of higher order recently introduced by Dattoli et al. is established, and Touchard polynomials of negative order are introduced and studied. 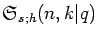Finally, a q-analogue $\mathfrak{S} _{s;h}(n,k\vert q)$ is introduced and first properties are established, e.g., the recursion relation and an explicit expression. 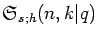It is shown that the q-deformed numbers $\mathfrak{S} _{s;h}(n,k\vert q)$ are special cases of the type-II p,q-analogue of generalized Stirling numbers introduced by Remmel and Wachs, providing the analogue to the undeformed case (q=1). Furthermore, several special cases are discussed explicitly, in particular, the case s=2 and h=-1 corresponding to the q-meromorphic Weyl algebra considered by Diaz and Pariguan.

Full version:  pdf,    dvi,    ps,    latex    

(Concerned with sequences A000110 A000369 A001497 A008275 A008277 A008297 A035342 A069223 A078739 A078740 A144299.)

Received July 17 2012; revised version received October 1 2012. Published in Journal of Integer Sequences, October 2 2012.

Return to Journal of Integer Sequences home page